Wo ein Vakuum ist, ist einfach nichts – das ist ja gerade die Definition von Vakuum. Sollte man jedenfalls meinen. Aber oft (und besonders in der Physik) sind die einfachen und offensichtlichen Dinge ja gern schlicht und einfach falsch – und so ist es auch mit dem Vakuum. In der Quantenmechanik ist ein Vakuum nicht mehr einfach “Nichts”, sondern – jedenfalls wenn man den populärwissenschaftlichen Darstellungen glaubt – voll von “Vakuumfluktuationen”, “virtuellen Teilchen” und solchem Zeugs. Leider sind diese Darstellung auch nicht so ganz korrekt, sondern nur (oft etwas schiefe) Bildchen des Vakuums. Hier will ich versuchen, etwas genauer zu erklären, was das Vakuum ist.
Die Hardcore-Hier-Wohnen-Drachen-Fans (falls es sowas gibt…) kennen das, was ich hier erklären will, schon: ich habe es sehr ausführlich in meiner Quantenfeldtheorie-Serie (siehe den Link auf Artikelserien rechts) erklärt. Aber die Erklärungen dort waren zum einen lang, zum zweiten etwas mathematisch und zum dritten weit hinten in einer langen (und nicht gerade einfachen) Serie versteckt. (Für mich hat sich die Serie auf jeden Fall aber gelohnt – denn zu einem guten Teil habe ich sie ja geschrieben, um mir selbst QFT beizubringen, und das hat ganz gut geklappt…) Deshalb versuche ich es hier noch einmal etwas kürzer zu erklären, denn Fragen nach dem Vakuum kommen ja immer wieder auf. (Weil ich dabei gelegentlich ein bisschen arg vereinfache, habe ich mal wieder Warnhinweise für diejenigen eingestreut, die schon ein bisschen mehr wissen.)
Das klassische Vakuum
Zunächst mal kann man sich natürlich fragen, wie man den Begriff “Vakuum” überhaupt definieren soll – unsere physikalischen Begriffe sind ja nicht naturgegeben, sondern menschengemacht, auch wenn sie mehr oder weniger gut mit natürlichen Phänomenen korrespondieren. In der klassichen Physik herrscht in einem Gebiet zunächst Vakuum, wenn man alle Teilchen daraus entfernt, so wie bei den berühmten Magdeburger Halbkugeln
Bild:public domain
Die einfachste Definition für ein Vakuum wäre also: “Ein Vakuum enthält keine Teilchen”.
Allerdings hat man dann im 19. Jahrhundert gemerkt, dass es nicht nur Teilchen gibt, sondern auch Felder, beispielsweise das elektrische oder magnetische Feld. Diese Felder enthalten auch Energie – wenn man also in einem Vakuum möglichst “Nichts” haben will, dann sollte es auch frei von solchen Feldern sein. Also: “Ein Vakuum ist ein materie- und feldfreier Raum”. Ein solches klassisches Vakuum ist also vollkommen leer (man könnte auch sagen, es ist nur Raum, aber ohne Inhalt). Ich bin hier historisch nicht ganz korrekt, denn es gab ja auch mal die Vorstellung des Äthers, der den ganzen Raum erfüllen sollte (also auch jedes Vakuum), aber diese Komplikation können wir hier ignorieren.
Quantentheorie: Teilchen und Felder
Wie überträgt sich nun diese “klassische” Definition in die moderne Physik, in der es ja die berühmten Quanteneffekte gibt (darüber habe ich ja schon viel geschrieben, klickt rechts bei Artikelserien, da sind einige meiner Texte zur Quantenmechanik gelistet)? Zunächst mal unterscheidet die Quantenphysik (genauer gesagt, die Quantenfeldtheorie) nicht zwischen Teilchen und Feldern. In der Quantenmechanik gibt es den oft verwendeten Begriff des “Welle-Teilchen-Dualismus'”, aber den braucht man eigentlich nicht, weil man alle Objekte (egal ob Licht oder Elektronen oder sonst etwas) mit Hilfe von “Quantenfeldern” beschreibt – deswegen heißt die Disziplin ja auch Quantenfeldtheorie, kurz QFT.
Die QFT ist ziemlich kompliziert (bei den Artikelserien findet ihr, wie gesagt, die Langfassung zum Thema), aber hier beschränken wir uns auf die einfachsten Aspekte. Was ist also ein Quantenfeld? Wenig überraschend ist es ein Feld, das mit den Mitteln der Quantentheorie beschrieben wird.
Das wirft natürlich die nächste Frage auf: was ist ein Feld? In der Physik ist ein Feld etwas, das an jedem Punkt im Raum (und zu jeder Zeit) einen bestimmten Wert hat. Beispiele für solche Felder kennt ihr aus dem Alltag, hier zum Beispiel ein Feld, das auf der Erdoberfläche definiert wird (aus Copyrightgründen habe ich das ursprüngliche Bild durch ein frei verfügbares ersetzt – also nicht wundern, dass in einem Artikel von 2013 ein Bild von 2015 drin ist…):
Von NOAA / National Weather Service – National Centers for Environmental Prediction – Climate Prediction Center
File: W!B: (overlay of weeks, see below) – www.nws.noaa.gov > Monitoring & Data > Global Climate Data > Global Regional Climate Maps > Europe [1], Gemeinfrei, Link
Die Temperatur ist eine Größe, die an jedem Punkt in Europa einen Wert hat – deswegen spricht man auch von einem Temperaturfeld.
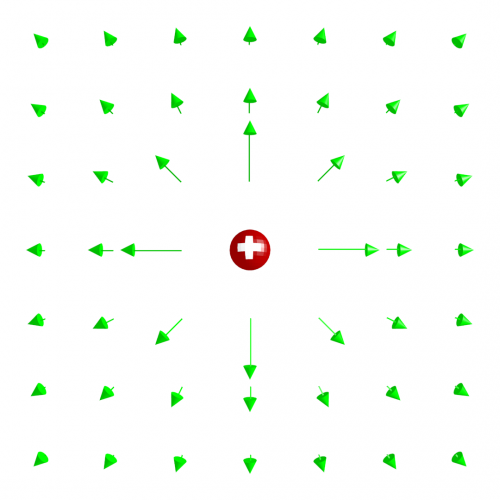
Ein anderes Beispiel ist ein elektrisches Feld – beispielsweise das elektrische Feld einer Punktladung (hier in zwei Dimensionen gezeichnet, damit es übersichtlicher ist):
Die Länge des Pfeils sagt, wie stark das Feld ist, die Richtung des Pfeils sagt, in welche Richtung das Feld zeigt. Natürlich kann ich das Feld nicht wirklich an jedem Punkt zeichnen, weil man dann nichts mehr erkennt, aber das Feld hat an jedem Punkt einen Wert.
Licht ist ja eine elektromagnetische Welle, man kann es deshalb (in der klassischen Physik) dadurch beschreiben, dass man an jedem Punkt im Raum und zu jedem Zeitpunkt sagt, wie groß jeweils der Wert des elektrischen und des magnetischen Feldes ist. (Tatsächlich benutzen die Physikerinnen meist eine andere Größe, das Viererpotential, weil das mathematisch einfacher ist, besonders in der QFT, aber mit dieser Komplikation ärgern wir uns hier nicht herum.)
Ähnliches gilt auch für Objekte wie Elektronen. Wir stellen uns Elektronen ja gern als kleine Kugeln vor (so wie die rote Kugel oben im Bild, nur dass die positiv geladen ist, nicht negativ – negativ geladene Teilchen sind natürlich blau, nicht rot). In der klassischen Physik ist das auch ein richtiges Bild, aber in der Feldtheorie beschreibt man ein Elektron nicht mehr als ein Teilchen, das sich an einem bestimmten Ort aufhält, sondern als Elektronenfeld – dieses Feld hat an jedem Punkt des Raumes einen Wert. Wenn ich weiß, dass sich ein einzelnes Elektron in einem kleinen Kasten aufhält, dann ist der Wert dieses Feldes im Kasten entsprechend ungleich Null, außerhalb gleich Null – jedenfalls wäre es bei einem “klassichen” Elektronenfeld so.
Hier kann man sich leicht verwirren lassen: Um das Vakuum quantentheoretisch beschreiben zu können, braucht man eine Quantenfeldtheorie. Was ich hier im Moment habe, ist noch eine klassische Feldtheorie, in der hat das Feld (wie ein Elektronenfeld oder ein elektrisches Feld) an jedem Punkt einen eindeutigen Wert, und wenn das Elektron “hier” ist, dann ist der Wert dieses Feldes überall woanders exakt gleich Null.
Leute, die schon etwas über Quantenmechanik wissen, sollten dieses Elektronenfeld auf keinen Fall mit der Elektronenwellenfunktion in der Quantenmechanik verwechseln – die beschreibt ein einzelnes Elektron quantenmechanisch, aber sie beschreibt nicht das Elektronfeld. Das Elektronfeld ist hier noch ein klassisches Feld (auch nicht ganz, 
weil es ein Spinorfeld ist, das erst quantisiert werden muss – eine echte klassische Theorie für das Elektron gibt es – anders als beim elektromagnetischen Feld – nicht.) Das wird oft verwirrend dargestellt – detailliert habe ich das hier erklärt.
Man könnte jetzt meinen, damit sei die Sache mit dem Vakuum ja wieder etwas einfacher geworden: Wenn alles durch solche Felder beschrieben werden kann, dann kann ich einfach sagen “Vakuum ist ein feldfreier Raum.” Im Vakuum ist der Wert des Feldes immer überall Null, und zwar für alle Felder, die es gibt (das elektrische und magnetische, das Elektronfeld und jedes andere Feld für all die anderen Elementarteilchen wie Quarks und Neutrinos ebenfalls). Das ist aber nicht richtig – bisher haben wir zwar Felder, aber wir haben die noch nicht mit den Mitteln der Quantentheorie beschrieben, das tun wir jetzt.
Quantenmechanische Überlagerungen
O.k., wir haben also jetzt ein Elektronfeld (oder ein elektromagnetisches Feld), das an jedem Punkt im Raum einen Wert hat. Damit sind wir aber noch nicht in der Quantentheorie angekommen – in der Quantentheorie haben Felder nämlich meist keine eindeutigen Werte, sondern befinden sich in Überlagerungszuständen. (Der Link erklärt dasmit der Überlagerung ausführlich, hier die Kurzfassung.)
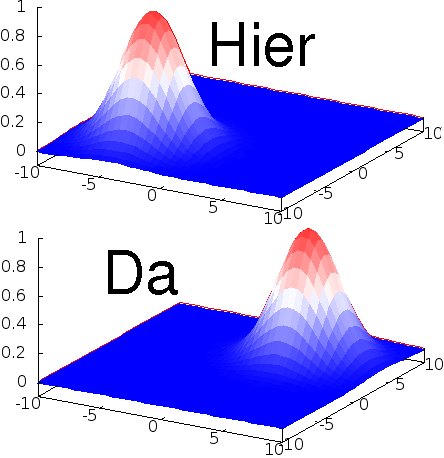
In der Quantentheorie kann man – außer wenn man gerade eine Messung gemacht hat und damit ganz sicher weiß, was los ist – nur Wahrscheinlichkeiten dafür angeben, dass ein System in einem bestimmten Zustand ist. Beispielsweise könnte ein Elektron entweder “hier” oder “da” sein – wenn es “hier” ist, dann hat das Elektronfeld einen großen Wert “hier”, wenn es “da” ist, hat es einen großen Wert “da”.
Das Bild ist etwas vereinfacht, weil das Elektron ja einen Spin hat, den ignoriere ich hier – ansonsten müsste das feld mehrere Spinorkomponenten haben, das wäre erstens unübersichtlich und ändert zweitens nichts am Prinzip.)
Wichtig ist hier, dass das Quantenfeld nicht einfach die Summe aus beiden Feldern ist. Vielmehr muss man für jede der beiden Möglichkeiten eine eigene Wahrscheinlichkeit angeben, die beiden Möglichkeiten sind aber zu unterscheiden. Wenn euch das verwirrt, denkt nochmal an das Temperaturfeld. Wenn es eine 50%-Wahrscheinlichkeit dafür gibt, dass morgen in Braunschweig 30° (freu) sind und 50% Wahrscheinlichkeit für 20° (kaaalt), dann ist das nicht dasselbe als wenn die Temperatur morgen 50° (oder 25°, wegen der 50%) ist, oder? Quantenmechanische Wahrscheinlichkeiten verhalten sich genauso, auch wenn sie – anders als beim Wetter – nicht einfach nur dadurch kommen, dass wir etwas nicht wissen.
Um den Zustand eines Feldes (beispielsweise des elektrischen Feldes oder des Elektronfeldes) in der QFT anzugeben, muss ich jetzt für alle möglichen Felder die Wahrscheinlichkeit angeben:
Mathematisch ist das ziemlich trickreich, weil es ja unendlich viele mögliche Funktionen gibt, die das Feld beschreiben können. Deswegen wird das genau so auch selten tatsächlich gemacht, sondern sich mit anderen Techniken (wie dem Pfadintegral oder der “kanonischen Quantisierung”) beholfen.
Also: Um einen Zustand eines Quantenfeldes anzugeben, müsst ihr alle möglichen Feldkonfigurationen hinschreiben und für jede davon eine Wahrscheinlichkeit angeben.
Ich habe mal wieder etwas vereinfacht,- genauer gesagt muss man für jede Feldkonfiguration nicht die Wahrscheinlichkeit, sondern die Wahrscheinlichkeitsamplitude angeben, die eine komplexe Zahl ist. Aber hier geht’s ja nur ums Prinzip, nicht um die Details. Außerdem habe ich etwas übertrieben: es reicht, wenn ihr einen vollständigen Satz von Feldkonfigurationen betrachtet also beispielsweise alle Fourierkomponenten. Das ist ähnlich in der Quantenmechanik – dort ist der Zustand eindeutig bestimmt, wenn ihr die Wahrscheinlichkeit für jeden mögliche Ort des Elektrons angebt, das ist dann gerade die Wellenfunktion. Aber Achtung: Es bekommt nicht einfach bloß die Fourierkomponente zur Wellenzahl k eine einzige Amplitude, sondern jeder mögliche Wert der Fourierkomponente hat eine Wahrscheinlichkeitsamplitude. Im Detail habe ich das auch in der QFT-Serie in den letzten beiden Teilen zum Thema Zustände erklärt.
Das Vakuum
Man könnte jetzt annehmen, dass der Vakuumzustand derjenige ist, bei dem die Wahrscheinlichkeit, dass unser Quantenfeld (wir betrachten erst mal nur ein Feld, beispielsweise das elektromagntische) überall gleich Null ist, gleich 1 ist und alle anderen Zustände, in denen das Feld irgendwo von Null verschieden ist, haben den Wert Null. Das sollte doch die beste Annäherung an die Idee des “feldfreien Raums” sein, oder? Das sähe etwa so aus:
Es gibt da nur ein klitzekleines Problem: Wenn ihr die Gleichungen der QFT verwendet, um diesen Zustand zu berechnen, dann stellt ihr etwas merkwürdiges fest: Er hat eine unglaublich hohe Energie und ist nicht – wie man meinen könnte – der energetisch günstigste Zustand. Würdet ihr also ein solches “Vakuum” irgendwo herstellen, wäre es nicht stabil, sondern würde ziemlich schnell in einen Zustand mit niedrigerer Energie übergehen.
Und das ist sicher nicht das, was wir uns unter einem Vakuum vorstellen – ein Vakuum sollte zumindest stabil sein und es sollte nicht mehr Energie enthalten als andere Zustände.
Deshalb ist man in der QFT auf die Idee gekommen, das Vakuum anders zu definieren: “Das Vakuum ist der Zustand mit der niedrigst-möglichen Energie.”
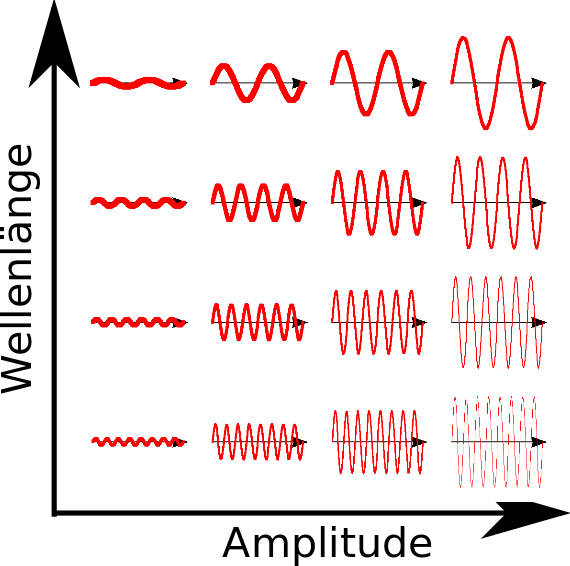
Und wie sieht dieser Vakuumzustand nun aus? Das ist zugegebenermaßen ziemlich kompliziert (und nahezu alle QFT-Bücher sagen dazu wenig bis nichts). Die genaue Erklärung findet ihr (wen wundert’s inzwischen noch…) in meiner QFT-Serie, aber zumindest eine grobe Idee will ich euch geben. Dieses Bild hier soll illustrieren, wie der Vakuumzustand aussieht. Jedes Teilbildchen gibt an, wie unser Feld aussehen könnte; die Dicke der Linie ist ein Maß für die Wahrscheinlichkeit:
Ich habe dabei die unterschiedlichen Feldkonfigurationen so sortiert, dass das ganze halbwegs übersichtlich bleibt, außerdem habe ich das Feld jetzt nur eindimensional entlang einer Linie gezeichnet, nicht wie sonst in zwei Dimensionen, einfach weil es dann etwas übersichtlicher wird: Von links nach rechts wird dabei die Amplitude (also der Wert des Feldes) immer größer, nach unten hin werden die Wellen immer kürzer. Ich habe dabei die Standard-Technik der Physik angewendet und das Feld als ebene Welle dargestellt. Ihr seht, dass große Abweichungen des Feldes vom Nullwert oder solche, die sich räumlich schnell ändern, unwahrscheinlich sind, während geringe Abweichungen vom Nullwert mit langer Wellenlänge eher wahrscheinlich sind.
Der Vakuum-Zustand eines Quantenfeldes hat folgende Eigenschaften:
Im Mittel ist alles gleich Null
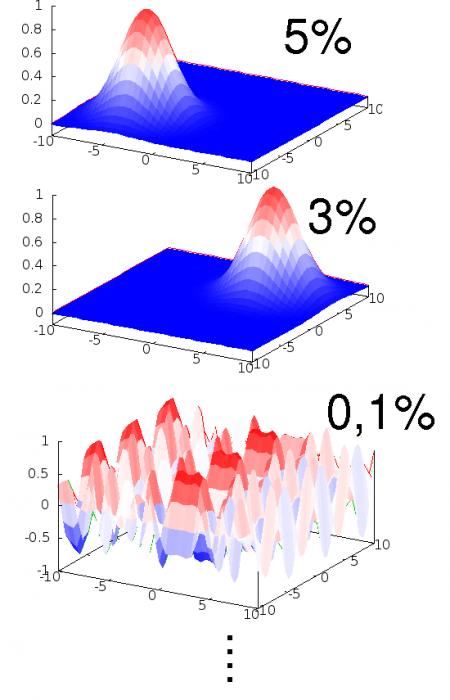
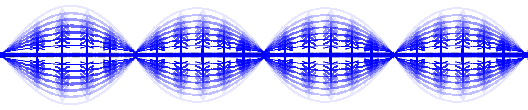
Nehmen wir als Beispiel das elektrische Feld. Wenn ich ein geladenes Teilchen in ein Vakuum bringe, dann sollte das teilchen nicht in eine Richtung gezogen werden. Die Wahrscheinlickeit, dass das elektrische Feld z.B. nach “oben” zeigt, sollte also genau so groß sein wie die, dass es nach “unten” zeigt. Das Feld hat zwar eine Wahrscheinlichkeit, von Null verschieden zu sein, aber wenn ich über alle Möglichkeiten mittele, dann sollte Null herauskommen. (In vornehmem Physiksprech heißt das “Der Erwartungswert des Feldes ist Null”.) Aus Platzgründen habe ich das im Bild oben nicht mit eingezeichnet – ihr könnt euch zu jeder der roten Kurven jeweils die dazu entgegengesetzte (die da einen berg hat, wo die gezeichnete ein Tal hat und umgekehrt) dazudenken, die hat dann genau dieselbe Wahrscheinlichkeit. Für eine bestimmte Wellenlänge kann man das auch so zeichnen (diesmal in blau, und alle unterschiedlichen Möglichkeiten zu einer Wellenlänge direkt übereinandergezeichnet):
Null ist der wahrscheinlichste Wert
Zwar gibt es eine Wahrscheinlichkeit, einen Wert des Feldes ungleich Null zu finden, doch von allen Möglichkeiten ist der Wert Null der wahrscheinlichste. (Achtung: Das heißt nicht, dass der Wert Null wahrscheinlicher ist als alle anderen Werte zusammengenommen – er ist nur wahrscheinlicher als jeder andere Wert. Wenn ich einen Würfel so fälsche, dass ich mit 20% Wahrscheinlichkeit eine 6 würfle und mit jeweils 16% jede der anderen Zahlen, dann ist 6 der Wahrscheinlichste Wert, aber in 4 von 5 Fällen werde ich trotzdem etwas anderes würfeln.) Im großen Bild seht ihr das daran, dass die Kurven mit kleinerer Amplitude dicker gezeichnet sind, in dem einfachen Bild mit einer einzigen Wellenlänge ist die dickste Linie genau die Null-Linie.
“Glatte” Felder sind wahrscheinlicher als “raue”
Anordnungen des Feldes, bei denen das Feld an benachbarten Punkten ähnliche Werte hat, sind wahrscheinlicher als solche, bei denen das Feld räumlich stark schwankt – je größer die Wellenlänge, desto wahrscheinlich ist so eine Feldkonfiguration. Weil starke räumliche Schwankungen (also kurze Wellenlängen) immer eine hohe Energie bedeuten, heißt das, dass Felder mit hoher Energie weniger wahrscheinlich sind als solche mit niedriger Energie.
Der Vakuumzustand ist raum- und zeitunabhängig
Das Vakuum sieht zu allen Zeiten und an allen Orten und auch für beliebige Beobachter immer gleich aus. Er ist zwar eine Überlagerung unterschiedlicher Möglichkeiten, aber diese Überlagerung ist zeitunabhängig. Das ist der Darstellung oben nicht ohne weiteres zu entnehmen – es sieht sogar so aus, als wäre es nicht so. Wenn ihr euch beispielsweise mit einer Rakete an einer Welle vorbeibewegt, dann schlägt die Relativitätstheorie zu und sorgt für eine Längenkontraktion, die Wellenlänge einer Welle ändert sich also. Auf den ersten Blick könnte man deshalb meinen, dass der Vakuumzustand vom Beobachter abhängen sollte, aber wenn man alles richtig ausrechnet stellt man fest, dass das nicht so ist. (Dass das Vakuum für alle immer gleich aussieht, ist in anderen Formulierungen der QFT einfacher zu sehen; ein weiterer Grund, warum die Darstellung, die ich hier wähle, selten verwendet wird.)
Das sind erst einmal die wichtigsten Eigenschaften des Vakuums.Es ist ein ziemlich komplizierter Überlagerungszustand aus unterschiedlichen Feldanordnungen, wobei solche mit hoher Energie (kurzer Wellenlänge oder großer Amplitude) nur wenig beitragen, also eine kleine Wahrscheinlichkeit besitzen, während Feldanordnungen mit kleiner Energie wahrscheinlicher sind.
Wenn ihr populäre Darstellungen zur Elementarteilchenphysik oder ähnlichem lest,lesen die sich allerdings meist ganz anders: Da ist das Vakuumt voller Fluktuationen, bei denen sich ständig “virtuelle Teilchen” aus dem Nichts bilden, die die Energieerhaltung für einen Moment verletzen, weil die Unschärferelation dies erlaubt. (Das liest man leider sogar in echten Lehrbüchern zur Quantenphysik oder bei Wikipedia.)
Tja, leider sind solche Erklärungen zwar hübsch und intuitiv, aber sie haben auch einen deutlichen Nachteil: Sie sind allenfalls als anschauliche Bildchen zu verstehen, aber letztlich sind sie mehr oder weniger falsch. Aber um zu erklären, was es damit auf sich hat, werde ich wohl mal wieder einen zweiten Teil bemühen müssen.
![[1]](https://www.cpc.ncep.noaa.gov/products/analysis_monitoring/regional_monitoring/wcmax1.png){kind=link}
Kommentare (97)