“Was ist ein Vakuum?” – “Ich hab’s im Kopf, aber ich komm nicht drauf.”
So ähnlich wie in diesem alten (zugegebenermaßen seeehr alten – aus dem Keller hört man dumpf das monotone Rattern der Bartwickelmaschine…) Scherz geht es mir im Moment. Im letzten Teil habe ich versucht, euch zu erklären, wie man sich das Vakuum vorstellen kann. Deutlich schwieriger scheint es zu sein, zu erklären, wie man sich das Vakuum nicht vorstellen kann oder sollte. Leider wimmeln Physikbücher und Internetseiten von Sätzen wie “Teilchen entstehen ständig aus dem Nichts und vergehen wieder” oder “Teilchen borgen sich Energie mit Hilfe der Unschärferelation”, die zwar nett klingen, aber leider letztlich falsch sind. Versuchen wir mal, etwas Licht ins Dunkel des Vakuums zu bringen.
Die Vakuumenergie
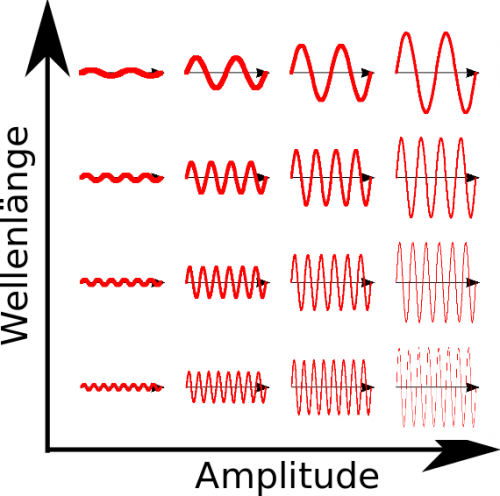
Nach dem, was ich letztes Mal geschrieben habe, ist das Vakuum ein Überlagerungszustand aus lauter unterschiedlichen Feldkonfigurationen. Solche mit großer Wellenlänge (wo sich das Feld nur sanft räumlich ändert) und mit kleiner Amplitude (also geringen Werten des elektrischen Feldes) sind dabei wahrscheinlicher (sie tragen stärker zum Zustand bei) als solche mit kurzer Wellenlänge oder mit großer Amplitude. Das habe ich in diesem Bildchen hier zusammengefasst:
Es ist immer etwas knifflig, sich solche Quantenfelder anschaulich vorzustellen, aber wir können es mit einer Analogie versuchen: Auch ein schwingendes Seil oder eine Saite kann unterschiedliche Wellenmuster bilden (denkt zum Beispiel an die Schwingungen einer Gitarrensaite). Wenn eine solche Gitarrensaite schwingt, dann hat sie natürlich auch eine Energie – deswegen muss man ja auch dran zupfen. Lässt man sie los, dann kommt sie irgendwann zur Ruhe. Eine quantenmechanische Gitarrensaite kommt aber nie wirklich zur Ruhe – sie ist immer in einem Zustand, in dem unterschiedliche Schwingungen überlagert sind, genau wie unser Vakuum. (In der Festkörperphysik hat man dasselbe mit den Schwingungen des Kristallgitters, den sogenannten “Phononen”.)
Und weil in Schwingungen Energie steckt, steckt auch in unserer Gitarrensaite noch Energie, selbst wenn sie scheinbar zur Ruhe gekommen ist. Diese Energie können wir nicht messen, dazu müssten wir sie der Gitarrensaite entziehen, aber das geht nicht, denn sie ist ja schon so sehr in Ruhe, wie es überhaupt nur geht.
Genau dasselbe gilt für unser Vakuum: Nach der Quantenfeldtheorie enthält das Vakuum Energie, aber diese Energie kann man – anders als in der Science fiction oder auch anderswo – dem Vakuum nicht entziehen, weil das Vakuum ja schon der Zustand mit der niedrigsten Energie ist. Man bezeichnet diese Energie deswegen naheliegenderweise als Vakuumenergie oder manchmal auch als Nullpunktsenergie – letzteres, weil sie am absoluten Nullpunkt, also wenn ihr ein System so weit abgekühlt habt, wie es nur geht, immer noch da ist.
Die Vakuumenergie ist für die QFT ein gewisses Ärgernis – in den Rechnungen spielt sie normalerweise keine Rolle, weil ja alle Prozesse sowieso im Vakuum stattfinden und man deswegen davon nichts merkt. Aber wenn man ihren Wert ausrechnet, dann kommt er in der Theorie als unendlich heraus – und selbst wenn man annimmt, dass die QFT irgendwann (auf der sogenannten Planck-Skala, also bei winzig kleinen Abständen, bei denen auch Gravitationseffekte in der QFT wichtig werden) nicht mehr gilt, ergibt sich immer noch ein riesiger Wert für diese Nullpunktsenergie.
Wie gesagt, in der QFT selbst ist dieser riesige Wert egal – wenn ich euch eine Fantastilliarde Euro aufs Konto einzahle, aber euer Konto so gebucht wird, dass ihr immer mindestens diese Fantastillioarde auf dem Konto haben müsst, dann merkt ihr davon nicht viel- wenn ihr eine Fantastilliarde plus Hundert Euro auf dem Konto habt, dann könnt ihr trotzdem nur Hundert Euro ausgeben.Ihr merkt also von dem Geld nichts. Obwohl – gibt es nicht doch einen Effekt, den wir bisher nicht berücksichtigt haben? Ihr müsstet ja – ein entsprechendes Konto vorausgesetzt – gigantisch viele Zinsen dafür bekommen.






Kommentare (112)