“Was ist ein Vakuum?” – “Ich hab’s im Kopf, aber ich komm nicht drauf.”
So ähnlich wie in diesem alten (zugegebenermaßen seeehr alten – aus dem Keller hört man dumpf das monotone Rattern der Bartwickelmaschine…) Scherz geht es mir im Moment. Im letzten Teil habe ich versucht, euch zu erklären, wie man sich das Vakuum vorstellen kann. Deutlich schwieriger scheint es zu sein, zu erklären, wie man sich das Vakuum nicht vorstellen kann oder sollte. Leider wimmeln Physikbücher und Internetseiten von Sätzen wie “Teilchen entstehen ständig aus dem Nichts und vergehen wieder” oder “Teilchen borgen sich Energie mit Hilfe der Unschärferelation”, die zwar nett klingen, aber leider letztlich falsch sind. Versuchen wir mal, etwas Licht ins Dunkel des Vakuums zu bringen.
Die Vakuumenergie
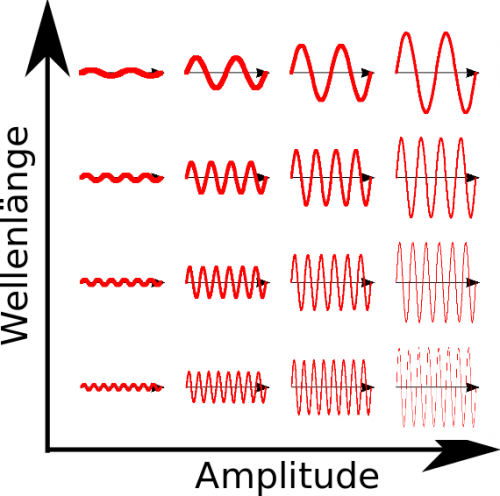
Nach dem, was ich letztes Mal geschrieben habe, ist das Vakuum ein Überlagerungszustand aus lauter unterschiedlichen Feldkonfigurationen. Solche mit großer Wellenlänge (wo sich das Feld nur sanft räumlich ändert) und mit kleiner Amplitude (also geringen Werten des elektrischen Feldes) sind dabei wahrscheinlicher (sie tragen stärker zum Zustand bei) als solche mit kurzer Wellenlänge oder mit großer Amplitude. Das habe ich in diesem Bildchen hier zusammengefasst:
Es ist immer etwas knifflig, sich solche Quantenfelder anschaulich vorzustellen, aber wir können es mit einer Analogie versuchen: Auch ein schwingendes Seil oder eine Saite kann unterschiedliche Wellenmuster bilden (denkt zum Beispiel an die Schwingungen einer Gitarrensaite). Wenn eine solche Gitarrensaite schwingt, dann hat sie natürlich auch eine Energie – deswegen muss man ja auch dran zupfen. Lässt man sie los, dann kommt sie irgendwann zur Ruhe. Eine quantenmechanische Gitarrensaite kommt aber nie wirklich zur Ruhe – sie ist immer in einem Zustand, in dem unterschiedliche Schwingungen überlagert sind, genau wie unser Vakuum. (In der Festkörperphysik hat man dasselbe mit den Schwingungen des Kristallgitters, den sogenannten “Phononen”.)
Und weil in Schwingungen Energie steckt, steckt auch in unserer Gitarrensaite noch Energie, selbst wenn sie scheinbar zur Ruhe gekommen ist. Diese Energie können wir nicht messen, dazu müssten wir sie der Gitarrensaite entziehen, aber das geht nicht, denn sie ist ja schon so sehr in Ruhe, wie es überhaupt nur geht.
Genau dasselbe gilt für unser Vakuum: Nach der Quantenfeldtheorie enthält das Vakuum Energie, aber diese Energie kann man – anders als in der Science fiction oder auch anderswo – dem Vakuum nicht entziehen, weil das Vakuum ja schon der Zustand mit der niedrigsten Energie ist. Man bezeichnet diese Energie deswegen naheliegenderweise als Vakuumenergie oder manchmal auch als Nullpunktsenergie – letzteres, weil sie am absoluten Nullpunkt, also wenn ihr ein System so weit abgekühlt habt, wie es nur geht, immer noch da ist.
Die Vakuumenergie ist für die QFT ein gewisses Ärgernis – in den Rechnungen spielt sie normalerweise keine Rolle, weil ja alle Prozesse sowieso im Vakuum stattfinden und man deswegen davon nichts merkt. Aber wenn man ihren Wert ausrechnet, dann kommt er in der Theorie als unendlich heraus – und selbst wenn man annimmt, dass die QFT irgendwann (auf der sogenannten Planck-Skala, also bei winzig kleinen Abständen, bei denen auch Gravitationseffekte in der QFT wichtig werden) nicht mehr gilt, ergibt sich immer noch ein riesiger Wert für diese Nullpunktsenergie.
Wie gesagt, in der QFT selbst ist dieser riesige Wert egal – wenn ich euch eine Fantastilliarde Euro aufs Konto einzahle, aber euer Konto so gebucht wird, dass ihr immer mindestens diese Fantastillioarde auf dem Konto haben müsst, dann merkt ihr davon nicht viel- wenn ihr eine Fantastilliarde plus Hundert Euro auf dem Konto habt, dann könnt ihr trotzdem nur Hundert Euro ausgeben.Ihr merkt also von dem Geld nichts. Obwohl – gibt es nicht doch einen Effekt, den wir bisher nicht berücksichtigt haben? Ihr müsstet ja – ein entsprechendes Konto vorausgesetzt – gigantisch viele Zinsen dafür bekommen.
Mit der Vakuumenergie ist es ähnlich – innerhalb der QFT merkt man nichts davon, aber statt Zinsen einzubringen müsste sie etwas anderes tun: Denn nach Einsteins berühmter Gleichung ist E=mc²; unsere Nullpunktsenergie entspricht also einer riesigen Masse (oder genauer gesagt, Massendichte), und die müsste sich bemerkbar machen. Stopft man nämlich das Weltall mit gigantisch viel Masse voll, dann müsste diese Masse nach der Relativitätstheorie die Expansion des Weltalls beeinflussen. Und weil die Masse wirklich riesig ist, wäre dieser Einfluss stark. So stark, dass das Weltall über die ersten paar Minuten seienr Existenz nicht hinausgekommen wäre, weil es sich durch die Vakuumenergie sofort wieder zusammengezogen hätte. Vergleicht man den theoretischen Wert der Vakuumenergie mit dem Wert, den sie maximal haben kann, damit das Universum seine heutige Form haben kann, dann stimmen diese beiden Zahlen nicht überein. Die Diskrepanz kann man am besten als faktor ausdrücken: Die theoretische Vakuumenergie laut QFT ist etwa 1Billion Billion Billion Billion Billion Billion Billion Billion Billion Billion mal zu groß – vermutlich die größte Abweichung zwischen Theorie und Experiment, die es je gegeben hat. (Und vermutlich ist der Faktor größer als eine Fantastlilliarde.) Ach ja, falls ihr jetzt die Idee habt, die Nullpunktsenergie könnte etwas mit der dunklen Energie zu tun haben, die die Astronomen so beschäftigt – da seid ihr nicht die ersten, bisher passt das aber nicht zusammen.
Natürlich hat man nach Ideen gesucht, wie man die Vakuumenergie loswerden kann. Eine davon ist zum Beispiel die Supersymmetrie – eine besondere Form der Quantenfeldtheorie, die viele neue Teilchen dazuerfindet, damit die Gleichungen hübscher werden. Ein großer Vorteil der Supersymmetrie liegt darin, dass in ihr die Nullpunktsenergie exakt verschwindet. Das liegt daran, dass es zwei unterschiedliche Arten von Teilchen gibt: Das eine sind die Bosonen, Teilchen wie das Photon oder die Gluonen, die für die Kernkraft verantwortlich sind. Das andere sind die Fermionen – die Teilchen, die wir als Materiebausteine ansehen wie Elektronen und Quarks. (Ja, irgendwann schreib ich auch noch mal was zum Teilchenzoo…) Rechnet man die Vakuumenergie für Fermionen aus, dann ist sie auch gigantisch groß – allerdings mit negativem Vorzeichen. (Und damit weiß niemand so recht etwas anzufangen.) In der Supersymmetrie gibt es jetzt für jede Bosonenart auch ein zugehöriges Fermion – dann heben sich all die vielen riesigen Energieterme alle sauber weg und nichts bleibt übrig. Das ist natürlich sehr nett und elegant – dummerweise gibt es bisher keine Anzeichen dafür, dass die SuSy (kurzform für Supersymmetrie) tatsächlich stimmt und die bisherigen Experimente am CERN sprechen eher dagegen. (Seit dem verlinkten Blogpost ist es tendenziell eher noch enger geworden…)
Es gibt noch ein paar andere Ideen zur Vakuumenergie (eine davon von Bob Klauber (die mich aber nicht überzeugt), dessen Buch ich gerade lese – ich stehe sogar in der Danksagung, weil ich letztes jahr mit Bob ein paar Ideen ausgetauscht habe und weil ich einen freundlichen Satz über das Buch geschrieben habe, der auch auf dem Cover steht…), aber letztlich ist sie ein offenes Problem in der QFT. Die meisten Theoretiker machen sich darum nicht so schrecklich viele Gedanken, und mit einem kleinen mathematischen Trick namens “Normalordnung” kann man die Vakuumenergie auch elegant – allerdings mathematisch meiner Ansicht nach letztlich ein bisschen illegal – aus der Theorie entfernen. (Hier gehen die Meinungen allerdings auseinander – siehe hierzu diese Diskussion, in der ich unter meinem US-Pseudonym poste (10 Hier-wohnen-Drachen-Taler für den, der die Herkunft meines Pseudonyms kennt)…)
Wie dem auch sei, da die Vakuumenergie immer da ist, kann man sie nicht in irgendeiner Form “anzapfen”.
Oder doch?
Der Casimir-Effekt
In den meisten Büchern oder Internetseiten wird zum Thema “Vakuum” ein experimenteller Nachweis zitiert – der Casimir-Effekt. Ich klaue das passende Bild bei Wikipedia

By Emok – Own work, CC BY-SA 3.0, Link
Beim Casimir-Effekt betrachtet man zwei Metallplatten, die genau parallel zueinander sind und die sehr dicht aneinander stehen. Das elektrische Feld kann auf solchen Platten nur senkrecht stehen, und das schränkt die möglichen Felder ein, die sich zwischen den Platten ausbilden können. Feldkonfigurationen mit einer Wellenlänge, die größer ist als der Abstand der Platten, sind beispielsweise nicht mehr möglich, auch solche nicht, bei denen z.B. nur 3,7 oder 12,9 Wellenlängen zwischen die Platten passen. (Auch die Wiki-Seite spricht übrigens von Teilchen, die auf grund der Energieunschärfe aus dem Vakuum erzeugt werden können – aber dazu komme ich noch, irgendwann.)
Schaut euch nochmal meine Veranschaulichung des Vakuums oben an. Wenn wegen der Metallplatten einige der Felder sich so nicht zwischen den Platten ausbilden können, dann fällt die entsprechende Zeile aus dem Diagramm heraus. Dementsprechend ist das Vakuum zwischen den Platten in einem anderen Zustand – es tragen weniger Möglichkeiten bei als beim ungestörten Vakuum. Und weil diese Möglichkeiten wiederum einen Beitrag zur Nullpunktsenergie leisten, ist die Nullpunktsenergie zwischen den Platten kleiner. Dieser Effekt wird um so größer, je dichter man die Platten zusammenschiebt. Man gewinnt also Energie, wenn die Platten sich annähern, und das bedeutet, dass sie sich anziehen. (Eine relativ einfache Rechnung dazu findet ihr im Buch von Zee “QFT in a nutshell” – er verwendet einen netten Trick, um die Feldenergie im Vakuum außerhalb der Platten geschickt einzubeziehen.)
Es gibt also eine winzige Kraft zwischen den beiden Metallplatten, die man mit genügend Messaufwand auch tatsächlich nachweisen kann. Und diese Messung bestätigt die Theorie auch sehr gut. Ein klarer experimenteller Nachweis der merkwürdigen Überlagerung unseres Vakuumzustands.
So steht’s jedenfalls in fast allen Büchern. Das kleine Problem dabei ist nur – ganz so einfach ist es nicht.
Der Physiker R.L. Jaffe hat sich 2005 seine eigenen Gedanken zum Casimir-Effekt gemacht. Insbesondere hat er überlegt, dass die Metallplatten ja irgendwie mit dem Feld (bzw. dem Vakuum) wechselwirken müssen – es können nicht einfach irgendwelche Platten sein, sondern sie müssen das Feld eben genau so beeinflussen, dass das elektrische Feld senkrecht auf den Platten stehen muss. Dazu müssen die Platten irgendwelche elektrischen Ladungen enthalten (die sich natürlich insgesamt ausbalancieren, weil die Platten elektrisch neutral sind.) Und das bedeutet, dass sich die Ladungen der beiden Platten gegenseitig beeinflussen können, indem sie über das Quantenfeld (wenn ihr wollt, könnt ihr von “virtuellen Photonen” sprechen) miteinander wechselwirken.
Rechnet man unter dieser Annahme mit den Mitteln der QFT aus, wie die beiden Platten sich beeinflussen, dann bekommt man dasselbe Ergebnis heraus wie bei der Rechnung mit den Vakuumfluktuationen. Die Rechnung ist insofern sogar etwas sauberer, als sie die Randbedingung (das Feld muss senkrecht stehen) direkt mit einbezieht und die Konsequenzen dieser Bedingung ausrechnet. Die Aussage, dass der Casimireffekt ein direkter Nachweis der Vakuumenergie ist, ist also zwar populär, aber zumindest problematisch, weil man dasselbe Ergebnis auch anders ausrechnen kann. (Das schließt aber natürlich nicht aus, dass beide Antworten richtig sind und dass beide letztlich äquivalent sind, sowas passiert in der Physik ja häufiger.)
Ihr seht, die Sache mit dem Vakuum ist komplizierter als man meistens liest – und deswegen wird es auch niemanden überraschen, wenn ich darüber noch einen weiteren Blogtext schreibe, dass meine Ideen der Art “ich könnte ja mal schnell was schreiben zu…” gern mal in längere Serien ausarten, ist ja nichts neues.
Disclaimer Wie so oft, wenn es um QFT geht, schreibe ich hier über Dinge, über die ich mir selbst gerade klar zu werden versuche. Wenn ihr also irgendetwas von dem, was ihr steht, eurem Prof in der Prüfung erzählt und dann durchfallt, übernehme ich keine Haftung dafür. (Nicht, dass ich das sonst täte…)






Kommentare (112)