Von Einstein zu Newton: II Beschleunigungen und Krümmungen

In dieser Mini-Serie will ich versuchen, den Zusammenhang zwischen der Allgemeinen Relativitätstheorie und der Newtonschen Physik herzustellen. Und zwar in genau der Richtung, die man in den meisten Darstellungen nicht zu sehen bekommt – wie bekommt man in der ART die ganz übliche Bewegung nach Newton, in der Kräfte wirken, wieder zurück?

Im ersten Teil haben wir uns angeschaut, was die Materie tut: im Newton-Bild übt sie Kräfte aus (man kann auch in modernerer Sprache sagen: Sie erzeugt ein Gravitationsfeld), in der ART beeinflusst sie die Krümmung von Raum und Zeit und sorgt insbesondere dafür, dass die zeit in der Nähe einer Masse langsamer vergeht (“matter tells spacetime how to curve”). Heute geht es dann darum, wie sich solche Felder oder Krümmungen auf die Bewegung von Teilchen auswirken. (Aber ich warne schon mal vor – den letzten Schritt machen wir dann in einem dritten Teil.)

Newton

Bei Newton ist die Welt einigermaßen einfach und überschaubar: Kräfte sorgen für Beschleunigungen (2. Newtonsches Gesetz), die Gravitationskraft beschleunigt also die Objekte. Für das, was gleich kommt, lohnt es sich aber, noch ein wenig genauer auf das Konzept der Beschleunigung zu gucken.

Eine Beschleunigung ist ja die Änderung einer Geschwindigkeit mit der Zeit – wenn ihr euch konstant mit 10m/s in dieselbe Richtung bewegt, dann beschleunigt ihr nicht. Die Geschwindigkeit wiederum ist die Änderung des Ortes mit der Zeit – wenn ihr immer am selben Ort seid, habt ihr keine Geschwindigkeit, wenn ihr jetzt hier seid und eine Sekunde Später 10 Meter weiter, dann war eure Geschwindigkeit eben genau 10m/s (jedenfalls im zeitlichen Mittel). Die Beschleunigung ist also die zeitliche Änderung der zeitlichen Änderung des Ortes mit der Zeit.

In diesem Artikel soll es ja darum gehen, wie sich Objekte im Schwerefeld bewegen. Die Beschleunigung eines Objekts in einem Gravitationsfeld ist ja (das haben wir im ersten Teil gesehen):

Wenn ein Teilchen also beispielsweise am Anfang an einem Ort x sitzt und die Geschwindigkeit Null hat, dann wirkt diese Beschleunigung. Einen Moment später hat diese Beschleunigung für eine Änderung der Geschwindigkeit gesorgt – wenn ihr Beispielsweise etwas fallen lasst, dann hat es nach einer Sekunde eine Geschwindigkeit von 9,81m/s, weil die Schwerebeschleunigung 9,81m/s² ist. Die Geschwindigkeit wiederum führt zu einer Änderung des Ortes. Das ist hier mathematisch schon ein klein wenig trickreich, weil sich die Geschwindigkeit ja ständig ändert. Für den Fall eines Teilchen im Schwerefeld habt ihr das vielleicht mal mit den entsprechenden Formeln in der Schule berechnet (ich hatte seinerzeit zwei geschlagene Monate lang das Thema “der schiefe Wurf” im Physikunterricht, das war schon kriminell langweilig und hatte ehrlich gesagt mit echter Physik auch wenig zu tun). Wenn sich die Beschleunigung während des Weges auch noch ändert (zum Beispiel, wenn ein Komet sich auf seiner Bahn der Sonne sehr stark nähert und dann wieder sehr weit entfernt), dann wird die Rechnung entsprechend komplizierter und man muss fiese Differentialgleichungen lösen. (Genau dafür hat Newton die Differentialrechnung ja erfunden – heutzutage würde man sich die Mühe möglicherweise gar nicht mehr machen und das System einfach numerisch im Computer simulieren….)

Zum Glück sind wir hier ja nicht in der Schule und müssen auch nichts wirklich ausrechnen – für uns reicht es zu wissen, dass sich das prinzipiell ausrechnen lässt. Die Beschleunigung unseres Objekts ist in jedem Moment gegeben durch die Größe S (die aktuelle Schwerebeschleunigung). Diese Beschleunigung ist gleich der Änderung der Geschwindigkeit, also der Änderung der Änderung des Ortes. Ohne jetzt auf die mathematischen Details einzugehen, schreibe ich das zumindest mal als Gleichung hin:

Das Symbol dv/dt steht dabei für die Änderung von v mit der Zeit t, entsprechend bedeutet d²x/dt², dass wir die Änderung der Änderung des Ortes x mit der Zeit t betrachten. (Dass man das eine “hoch-zwei” ² an das d und das andere an das t schreibt, sieht vielleicht komisch aus, ist aber so Konvention.) Also: S gibt die Änderung der Geschwindigkeit und damit die Änderung der Änderung des Ortes mit der Zeit an. Eine solche Gleichung nennt man eine Bewegungsgleichung – wenn ihr wisst, wo ein Teilchen am Anfang ist und welche Geschwindigkeit es hat, dann könnt ihr seine Bewegung vorhersagen.

Bisher habe ich allerdings noch die Richtungen ignoriert – wenn zum Beispiel ein Planet um die Sone kreist, dann wirkt die ganze Zeit eine Beschleunigung auf den Planeten (so wie ich es neulich für den Mond erklärt habe), aber die Beschleunigung und die Geschwindigkeit haben eine Richtung. Das kann man in der Gleichung dadurch berücksichtigen, dass man die Buchstaben, die nicht bloß für eine Zahl stehen, fett druckt:

Auch der Ort gehört fettgedruckt, weil der ja auch nicht bloß eine Zahl ist – auf der Erde zum Beispiel gibt man einen Längen- und Breitengrad an, außerdem noch die Höhe über dem Erdboden. Insgesamt braucht man also drei Zahlen, um den Ort festzulegen. In der Relativitätstheorie gehören ja Raum und Zeit untrennbar zusammen, deswegen nimmt man dort gleich vier Zahlen, drei für den Ort, eine für die Zeit. (Mathematisch etwas genauer habe ich das vor langer Zeit mal hier erklärt.)

Koordinaten und Krümmungen

Bevor wir uns anschauen, wie am Ende dieselbe Gleichung aus der ART herauskommt (obwohl es dort gar keine Gravitationskraft gibt, sondern nur die Raumzeitkrümmung), gibt es erstmal einen kleinen Umweg. Gleich bekommen wir es ja mit der Raumzeitkrümmung zu tun (wobei im Grenzfall nach Newton nur der Einfluss der Zeitdilatation relevant ist), und sowas ist ja immer etwas schwer anschaulich zu fassen. Also betrachten wir erst einmal die fast schon kanonische Analogie für die Raumzeitkrümmung: Die Krümmung der Erdoberfläche.

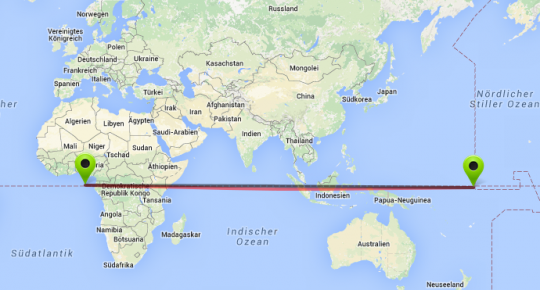
Stellt euch vor, ihr bewegt euch von einem Punkt auf dem Äquator zum genau gegenüberliegenden Punkt auf der Erdoberfläche. In der Ebene ist die kürzeste Verbindung zwischen zwei Punkten eine Gerade, und die ist eindeutig. Auf einer Kugel ist die kürzeste Verbindung ein sogenannter Großkreis – beispielsweise der Äquator. Ihr könnt also entlang des Äquators fliegen (Das Bild stimmt nur näherungsweise, aber es gibt hoffentlich die richtige Idee. Gemacht mit diesem Onlinerechner)

Nehmen wir an, ihr braucht 20 Stunden für den Flug, das macht dann eine Geschwindigkeit von 1000km/h, etwas schneller als ein handelsübliches Flugzeug. Wie ich oben ja schon erwähnt habe, kennzeichnet man Punkte auf der Erde mit ihren Längen- und Breitengraden – das ist deswegen praktisch, weil die eine Richtung dann immer die Ost-West-Richtung und die andere die Nord-Süd-Richtung ist. Eure Geschwindigkeit beträgt also 1000km/h nach Osten, und 0km/h nach Norden. Eure Beschleunigung ist also Null. Als Pilotin habt ihr es einfach – ihr fliegt konstant nach Osten.

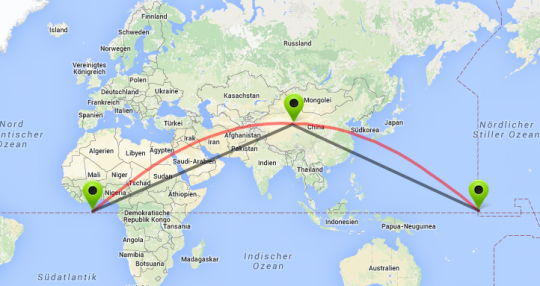
Alternativ könnt ihr aber auch eine andere Route nehmen, denn auf der Erde ist die kürzeste Verbindung zwischen zwei Punkten nicht immer eindeutig. Ihr könnt beispielsweise erst einen Punkt in China ansteuern und dann von dort aus weiterfliegen:

Obwohl das auf der Karte deutlich weiter aussieht, ist es das nicht – die Strecke ist genauso lang (naja, fast, ganz sauber habe ich die Punkte nicht getroffen). Mit einem Stück Schnur und einem Globus (zur Not tut es auch eine Orange) könnt ihr euch überzeugen, dass das wirklich so ist.

Wenn ihr aber Pilotin seid, dann ist es jetzt alles andere als einfach, wenn ihr diese Route nehmen wollt. Ihr fliegt erst nach Nordosten, müsst aber dabei immer mehr nach Osten abknicken, bis ihr dann irgendwo in China für einen Moment exakt nach Osten fliegt. Dann geht es weiter nach Südosten, wobei die Süd-Komponente eurer Geschwindigkeit immer größer wird.

Wenn ihr euren Ort also mit Längen- und Breitengraden beschreibt (also die Himmelsrichtungen verwendet), dann bedeutet das, dass sich eure Geschwindigkeit ständig ändert – zwar nicht von der Größe her (die ist immer 1000km/h), aber von der Richtung her. Anfangs hat die Geschwindigkeit eine Komponente nach Norden (ein paar 100km/h) und eine nach Osten, aber die Nord-Komponente der Geschwindigkeit wird immer kleiner, die Ost-Komponente größer. Dann ist die Nord-Komponente der Geschwindigkeit Null, wenn ihr in China seid und wird dann negativ. Ihr werdet also die ganze Zeit beschleunigt.

Kann das angehen? Nach Newton gehört zu jeder Beschleunigung eine Kraft – aber müsst ihr tatsächlich gegen irgendeine Kraft anarbeiten, um auf dieser Route eurer Flugzeug zu fliegen und nicht immer weiter nach Nordosten zu fliegen, wohin eure anfängliche Geschwindigkeit zeigte? Nein, natürlich müsst ihr das nicht. Die Beschleunigung hier ist zunächst mal nur eine Schein-Beschleunigung, weil ihr ein ungeschicktes Koordinatensystem gewählt habt. Ihr könntet ja einfach ein anderes Koordinatensystem definieren, bei dem der “Äquator” genau entlang eurer Flugroute verläuft, dann hättet ihr die ganze zeit wieder eine konstante Geschwindigkeit in dieser neuen “Ost-West-Richtung”. Ihr könnt euch auch vorstellen, die Erde hätte eine ganz glatte perfekte Oberfläche und ihr würdet eine Kugel losrollen lassen – die würde dann dem Großkreis folgen, in der Richtung, in der ihr sie gestartet habt, ohne dass ihr dazu eine Kraft braucht um sie auf dem Großkreis zu halten.

[Nebenbemerkung, ist für den Rest des Artikels nicht so wichtig, aber instruktiv, wenn man über die ART nachdenkt. Alternativ könnt ihr natürlich auch die Route über den Nordpol nehmen. Vom Äquator (bei 0°) fliegt ihr zum Nordpol (bei 90°). Dabei bleibt der Längengrad konstant. Dann fliegt ihr wieder vom Nordpol (bei 90°) zum Äquator (bei 0°) – dabei ist der Längengrad jetzt um 180° größer geworden. Die erste Hälfte der Strecke fliegt ihr also mit einer Geschwindigkeit von 1000km/h nach Norden, der Längengrad ändert sich nicht. Den zweiten Teil der Strecke fliegt ihr mit -1000km/h nach Norden (weil ihr nach Süden fliegt), der Längengrad ändert sich wieder nicht. Genau am Nordpol passiert etwas seltsames – hier schlägt der Längengrad um und ändert sich um 180°, und eure Geschwindigkeit ändert sich schlagartig von +1000km/h auf -1000km/h. Genau am Nordpol habt ihr deswegen – rein rechnerisch – eine unendliche Beschleunigung. Natürlich passiert am Nordpol tatsächlich überhaupt nichts mit euch, von der unendlichen Beschleunigung merkt ihr nichts. Es handelt sich um eine Auswirkung der für diesen Fall ungünstig gewählten Koordinaten mit Längen- und Breitengraden; würdet ihr die andersherum definieren, beispielsweise mit einem Ost-Pol und einem West-Pol, dann wäre es der Weg entlang des Äquators, bei dem etwas seltsames passieren würde, während der Weg über den Nordpol unproblematisch wäre. Solche “Koordinatensingularitäten” gibt es auch in der ART – das berühmteste Beispiel ist der Ereignishorizont eines Schwarzen Lochs, wenn man das Loch in sogenannten “Schwarzschild”-Koordinaten beschreibt. Auch da passieren scheinbar seltsame Dinge – aber nur, weil die Koordinaten ungünstig gewählt sind. Ein bisschen mehr dazu habe ich hier geschrieben.  ]

Aber wenn das nur am dumm gewählten Koordinatensystem liegt, ist es dann nicht ein Scheinproblem? Nein, ist es nicht. Denn ihr könnt zwar für jeden Großkreis, auf dem ihr fliegt, immer ein Koordinatensystem finden, bei dem man sofort sieht, dass ihr nicht beschleunigt, aber ihr könnt kein Koordinatensystem finden, bei dem das für alle Großkreise funktioniert. Entweder der Weg entlang des Äquators ist einfach oder der Weg über China – bei beiden geht es nicht. Und genau das liegt an der Krümmung der Erdoberfläche.

Im Newtonschen Gesetz (“jede Beschleunigung wird durch eine Kraft verursacht”) mussten wir solche Probleme nicht berücksichtigen, weil wir immer ein Koordinatensystem finden können, bei dem jede “echt” unbeschleunigte Bewegung auch so beschrieben werden kann. (Das sagt ja gerade das erste Newtonsche Gesetz: “Ein Körper, auf den keine Kraft wirkt, bewegt sich mit konstanter Geschwindigkeit, also entlang einer geraden Linie.”) Genau das geht aber in einem gekrümmten Raum (oder einer gekrümmten Raumzeit) nicht.

Die Analogie zur ART ist auch insofern gut, als ihr auch dort für ein frei fallendes Teilchen immer ein Koordinatensystem finden könnt, bei dem dieses Teilchen unbeschleunigt ist und auch keine Kräfte erfährt – nämlich das System, wo dieses Teilchen in Ruhe ist und keine Geschwindigkeit hat. Ihr könnt nur nicht erwarten, dass ein anderes frei fallendes Teilchen in demselben System ebenfalls unbeschleunigt ist, weil die Bahnen frei fallender Teilchen keinen konstanten Abstand haben, wenn eine Masse in der Nähe ist. (Zwei Steine, die ihr in gleicher Höhe loslasst, nähern sich an, weil sie beide auf den Erdmittelpunkt zufallen, zwei Steine in unterschiedlicher Höhe entfernen sich, weil der untere etwas stärker von der Erde angezogen wird als der obere.)

Wir können uns noch kurz überlegen, wovon die Beschleunigung unseres Flugzeuges auf der China-Route (gemessen in normalen Längen- und Breitengraden) abhängt. Zum einen natürlich von der Krümmung der Erde. Wenn ihr zum Beispiel den Erdradius halbiert, und mit 1000km/h am Anfang nach Nordosten fliegt, dann müsst ihr natürlich entsprechend stärker nachkorrigieren, wenn ihr nach Kompass fliegt.  Zum anderen geht aber auch die aktuelle Geschwindigkeit hier ein, denn wenn ihr nur sehr langsam fliegt, müsst ihr eure Nord-Süd-Abweichung nur sehr langsam korrigieren, je schneller ihr fliegt, desto öfter müsst ihr auf den Kompass schauen, um eure Richtung beizubehalten.

So, heute ist ein guter Tag, um mal wieder meine alten “Achtung, jetzt wird es mathematisch”-Schilder rauszukramen. Falls ihr die Mathematik nicht so interessant findet, könnt ihr bis zum Aufhebungsschild überspringen.

Wenn man mathematisch etwas genauer hinschaut, dann sieht man, dass die Geschwindigkeit zweimal eingeht – je schneller ihr fliegt, desto schneller müsst ihr die Größe, um die es geht, nachkorrigieren. Das wäre aber bei jeder (vektoriellen) Größe der Fall, die ihr auf der gekrümmten Kugel betrachtet. Die Größe, um die es geht, ist aber die Änderung der Geschwindigkeit, deswegen geht die hier noch einmal ein. Deshalb sieht die Formel für die Schein-Beschleunigung auf der Kugeloberfläche so aus (nicht erschrecken):

Ich habe das hier in Komponenten auseinandergeschrieben -links steht also die Komponente i der Beschleunigung – das i kennzeichnet also die Geschwindigkeit bzw. Beschleunigung in Nord-Süd- oder in Ost-West-Richtung. (Wenn ihr eine Geschwindigkeit von 1000km/h genau nach Nordosten habt, dann hat die Geschwindigkeit eine Komponente von 707km/h in Nord-Süd und von 707km/h in Ost-West-Richtung.) Rechts stehen auch zwei Geschwindigkeitskomponenten in der Formel, davor steht das fies aussehende Γ (in der ART bekannt als “Christoffel-Symbol”) mit gleich drei Indices. Das Γ gibt genau an, wie schnell ihr die Komponenten eures Beschleunigungsvektors drehen müsst, damit ihr euch die ganze Zeit auf einem Großkreis bewegt. Es hängt von der krümmung der Fläche, auf der wir uns bewegen, ab, aber natürlich auch vom gewählten Koordinatensystem (auf der Äquator-Route wären die relevanten Γ-Werte alle Null, weshalb wir dort keine Beschleunigung in unserem Koordinatensystem wahrnehmen.

Fazit

Ja, es ist mal wieder alles viel länger geworden als ursprünglich geplant – die Darstellung der Bewegung in der ART vertage ich deshalb auf einen dritten Teil (ursprünglich dachte ich, das würde alles in einen einzigen Text passen…). Deshalb hier ein kurzes Fazit der wichtigsten Punkte.

In der Newtonschen Physik bekommen wir eine Bewegungsgleichung für die Beschleunigung, die sich aus der Gravitationskraft ergibt.

Betrachtet man Bewegungen auf gekrümmten Flächen, muss man beim Bewegen berücksichtigen, dass sich die Koordinaten auf einer gekrümmten Fläche oft seltsam verhalten. Man kann zwar z.B. auf der Kugel ein Koordinatensystem finden, bei dem die Bewegung auf einem Großkreis einfach ist (denkt an den Äquator) – aber so ein System gibt es nicht global, so dass es für alle Teilchen, die kräftefrei sind, funktioniert. Auf einem gekrümmten Raum bekommt man deswegen -wenn man ein übliches Koordinatensystem nimmt, wie etwa Nord-Süd, Ost-West – eine Gleichung für die “Beschleunigung” auch dann, wenn gar keine Kräfte wirken. Das war bei Newton kein Problem, weil es im Newtonschen Raum immer ein Koordinatensystem gibt, bei dem alle kräftefreien Bewegungen einfache gerade Linien sind – aber auf einem gekrümmten Raum geht das nicht.

Und jetzt müssen wir das nur noch auf die Raumzeit übertragen – denn in der ART ist es nicht die Krümmung des Raums, sondern die Änderung der Zeit, die dafür sorgt, dass wir am Ende die Bewegungsgleichung nach Newton wiederbekommen.