Ich habe gerade etwas Nettes entdeckt – vermutlich haben das schon 1000 andere vor mir getan, aber das tut der Sache ja keinen Abbruch.
Es geht um Abstände im Raum und in der Raumzeit und vor allem darum, wie man sie sich veranschaulichen kann.
Fangen wir mit Abständen im Raum an, also mit der euklidischen Geometrie. Stellt euch vor, ihr seid auf einer Ebene mit einer x- und einer y-Achse unterwegs. Euch interessiert der Abstand des blauen Punkts vom Ursprung des Koordinatensystems (den Abstand bezeichnen wir mit “s”):
O.k., das ist in diesem Fall einfach, weil der Abstand einfach gleich dem x-Wert der Koordinate des blauen Punkts ist und man ihn ja direkt ablesen kann. (Wenn der x-Wert bei einer Koordinate von 2 cm liegt, dann ist der Abstand 2cm).
Man kann sich den Abstand aber auch anders veranschaulichen, nämlich über eine Fläche: Das Quadrat des Abstands ist gleich der Fläche des gelben Quadrats (Achtung, damit keine Missverständnisse aufkommen: Hier und im Folgenden ist s² immer die schrafierte Fläche):
Immer noch ziemlich trivial (und ein bisschen sinnlos, oder)? Interessanter wird es, wenn der blaue Punkt nicht mehr auf der x-Achse liegt, sondern irgendwo:
Jetzt zeichnen wir zwei Quadrate, eins mit der Kantenlänge passend zum x-Wert (gelb), eins passend zum y-Wert (rot). Die schraffierte Fläche ist jetzt proportional zum Quadrat des Abstands s, also zu s². Man kann natürlich stattdessen auch ein Quadrat über die Kante s selbst zeichnen, nach dem Satz des Pythagoras hat das dieselbe Fläche: s²=x²+y²:
Fragt ihr euch immer noch, was das ganze soll? Dann machen wir jetzt den Sprung von der euklidischen Ebene zum Raumzeit in der speziellen Relativitätstheorie. (Die sogenannte Minkowski-Metrik.) Dort haben wir (der Einfachheit halber, sonst muss ich in 3D zeichnen) eine räumliche Dimension x und eine zeitliche Dimension t. Dabei misst man die räumliche Distanz in Lichtsekunden (eine Lichtsekunde=300000km, weil das Licht pro Sekunde 300000 Kilometer zurücklegt – genau genommen 299792,458, aber so pingelig muss man nicht sein) und die zeit in Sekunden, dann werden die Diagramme besonders einfach zu zeichnen.
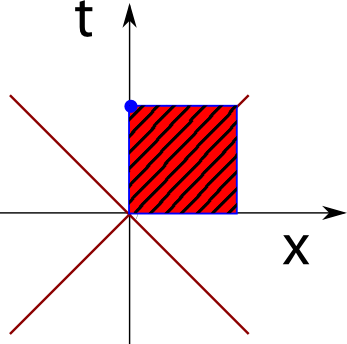
Setzen wir unseren blauen Punkt erst einmal auf die Zeitachse – er ist also bei x=0, aber in der Zukunft (wir betrachten eine Linie vom Ursprung in der Mitte zu einem Punkt am selben Ort in der Zukunft – diese Linie (“Weltlinie”) könnte also die Bewegung eines Teilchens vom Ursprung zu diesem Punkt beschreiben, wobei sich das Teilchen hier gar nicht bewegt, weil sich der Ort ja nicht ändert):
Das rote Quadrat hat jetzt eine Fläche, die gleich t² ist – logischerweise.
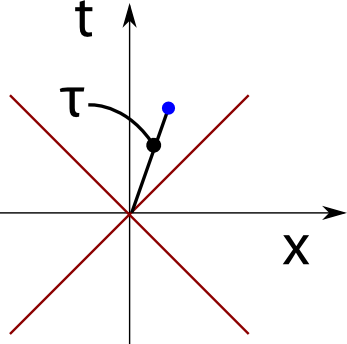
Aber jetzt wird es interessant: Wenn sich das Teilchen sich nicht nur in der Zeit bewegt, sondern auch im Ort, dann sieht das Bild so aus (Ignoriert für den Moment die beiden diagonalen roten Linien, die kommen gleich):
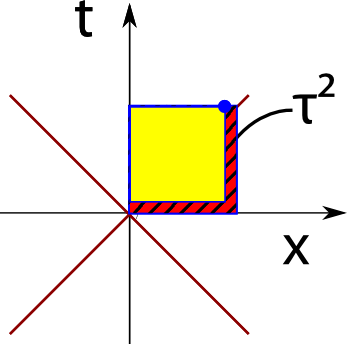
Der blaue Punkt ist der Raumzeitpunkt, zu dem das teilchen entlang der schwarzen Linie vom Ursprung aus geflogen ist. Das Teilchen war also am Anfang am Koordinatenursprung und hat sich dann zu einem Punkt mit größerem x-Wert hin bewegt. Der Raumzeit-Abstand des blauen Punkts zum Ursprung ist jetzt τ (der griechische Buchstabe “tau”). Wenn das Teilchen eine Uhr bei sich trägt, dann ist dieses τ gleich der Zeit, die für das Teilchen verstrichen ist, seit es vom Ursprung losgeflogen ist. In der Relativitätstheorie gibt es ja die Zeitdilatation – der Wert von τ ist also kleiner als t. Wie kann man sich das veranschaulichen? am besten, indem man wieder zwei Quadrate zeichnet:
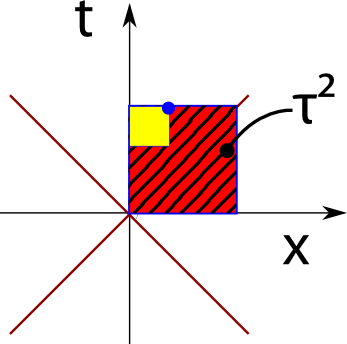
Die Konstruktion ist ähnlich wie oben in der Ebene, aber jetzt wird die Fläche des kleineren Quadrates (mit Kantenlänge x) von der des größeren abgezogen. Die schraffierte Fläche ist jetzt proportional zu τ², denn es gilt τ² = t²-x².
Wenn unser Teilchen sich schneller bewegt, entfernt sich der blaue Punkte weiter in x-Richtung. Dann wird die schraffierte Fläche immer kleiner
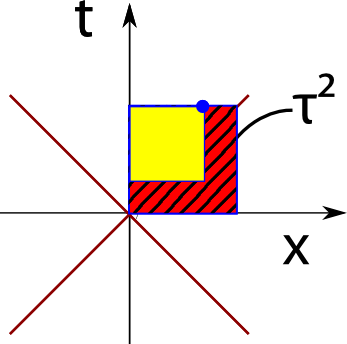
und kleiner
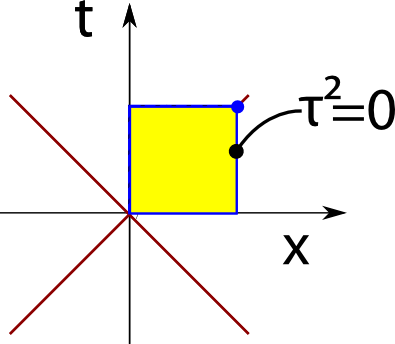
und verschwindet schließlich ganz:
Je schneller das Teilchen sich vom Ursprung entfernt, desto kleiner wird τ, desto weniger Zeit vergeht also für das Teilchen. Das ist genau die Zeitdilatation und mit dieser einfachen Konstruktion kann man sie direkt veranschaulichen. Im letzten Bild ist τ=0, für das Teilchen vergeht also gar keine Zeit. Wie das angehen kann? Im letzten Bild landet der blaue Punkt ja auf der diagonalen roten Linie – das Teilchen hat sich also in einer Sekunde im genau eine Lichtsekunde bewegt, mit anderen Worten, es ist mit Lichtgeschwindigkeit unterwegs. Licht aber hat keine Eigenzeit. (Ich vermeide die Aussage “für Licht vergeht keine Zeit”, weil Licht nichts ist, das eine Zeit messen oder eine Uhr bei sich tragen kann – es gibt kein sinnvolles Bezugssystem, in dem Licht ruht.)
Noch weiter nach rechts kann man den Punkt auch schieben, aber dann müsste man die Fläche negativ rechnen, weil das gelbe Quadrat größer wird als das rote. So kann sich allerdings kein Teilchen bewegen, dazu müsste es mit Überlichtgeschwindigkeit unterwegs sein. (Man kann natürlich die Konstruktion umdrehen und das rote vom gelben Quadrat abziehen, das wäre dann in der SRT ein “raumartiger” Abstand, aber das erkläre ich hier nicht – diejenigen die das kennen, dürften es sofort einsehen, alle anderen sind vermutlich eher verwirrt…)
Ich finde die Konstruktion hübsch, weil sie zum einen die Analogie und die Unterschiede zur gewöhnlichen Geometrie aufzeigt, und weil man zum anderen unmittelbar sieht, wie die Zeit für das Objekt immer langsamer vergeht, weil die schraffierte Fläche kleiner wird. Ich bin aber gespannt auf Eure Meinung – ist das eine hilfreiche Veranschaulichung oder ist die Konstruktion zu wirr?
PS: Ja, hier auf dem Blog ist es im Moment sehr still, im letzten Monat gab’s nur einen Post. Das liegt nicht nur daran, dass ich ne Woche verreist war und ein paar Tage krank, sondern vor allem daran, dass ich gerade in meiner Freizeit Dinge schreibe, die nicht für den Blog sind. Worum es da geht, verrate ich aber noch nicht.










Kommentare (57)