Wurmlöcher dürfen ja in der Science-Fiction nicht fehlen, um mal schnell von A nach B zu reisen. Sie sind gewissermaßen Abkürzungen durch den Raum und sollen zwei entfernte Bereiche des Universums so miteinander verbinden, dass man schnell vom einen zum anderen gelangt. Der Begriff kommt von der Analogie zu einem Apfel: Wenn ein Wurm ein Loch durch den Apfel frisst, dann könnt ihr von einer Seite zur anderen reisen und habt einen kürzeren Weg als wenn ihr über die Oberfläche des Apfels krabbelt. (Falls ihr zu groß seid, um auf einem Apfel herumzukrabbeln, denkt euch einfach einen Tunnel durch die Erde von Deutschland nach Neuseeland – durch den müsstet ihr nur etwa 12000 Kilometer zurücklegen statt 20000 auf der Erdoberfläche.)
Auch in der Wissenschaft werden Wurmlöcher aber diskutiert; ein aktuelles Beispiel ist dieser Artikel von Florian. Stellt sich natürlich die Frage: Was genau sind Wurmlöcher eigentlich und sollten wir annehmen, dass es sie gibt?
Wurmlöcher sind (theoretisch) möglich
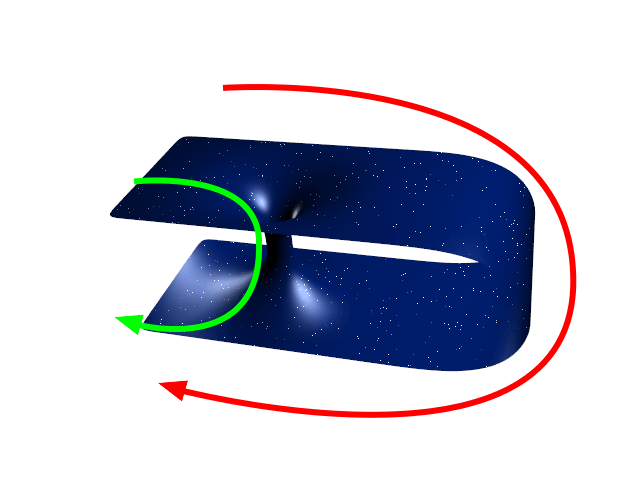
Die Idee zu Wurmlöchern stammt aus der Allgemeinen Relativitätstheorie (kurz ART). Die sagt uns ja, dass die Gravitation “eigentlich” nichts anderes ist als eine Krümmung der Raumzeit. (Zum Glück können wir die Zeit hier ignorieren und uns nur mit dem Raum beschäftigen.) Wenn der Raum aber gekrümmt sein kann (so wie zum Beispiel die Oberfläche einer Kugel gekrümmt ist), dann kann er möglicherweise auch eine komplizierte Struktur haben, beispielsweise eine, wo zwei entfernte Bereiche des Raums auf einem kurzen Weg miteinander verbunden sind, so wie in diesem Bild:
Von Panzi – English Wikipedia, CC BY-SA 3.0, Link
Der flache Teil oben und unten soll das normale Universum darstellen, beispielsweise könnte oben die Erde und unten die Andromeda-Galaxie sein. Ihr könnt den ganzen Weg durch das normale Universum nehmen, oder ihr nehmt die Abkürzung durch das Wurmloch. Theoretisch kann diese sehr kurz sein, so dass ihr innerhalb von Wochen oder Monaten effektiv Millionen Lichtjahre zurücklegen könnt.
Dass so etwas theoretisch möglich ist, liegt an der zentralen Gleichung der ART, der Einsteinschen Feldgleichung. Diese setzt die Raumkrümmung an einem Ort in direkte Beziehung zu Masse, Energie und Druck an diesem Ort. Die Gleichung ist also in diesem Sinne lokal, jede Wirkung der Gravitation (also der Raumzeitkrümmung) breitet sich deshalb von dort aus, wo Materie (bzw. Energie) ist. (Service-Hinweis: Nein, dieser Artikel ist keine Einführung in die ART, wenn ihr so etwas sucht, findet ihr reichlich bei den Artikelserien hier im Blog, rechts in der tag-Wolke, oder in meinem Buch zum Thema. Ich vereinfache hier deshalb ein wenig.)
Damit die Gleichung funktioniert, muss der Raum (oder genauer die Raumzeit) bei kleinen Abständen betrachtet “glatt” sein – er darf keine Zacken oder Spitzen oder Risse haben. Guckt euch das Bild des Wurmlochs oben noch einmal an: In der Umgebung jedes Punkts könnt ihr sehen, dass der Raum dort ganz normal aussieht – in diesem Fall zweidimensional, weil das Bild eine Dimension unterschlägt, denn vierdimensionales Zeichnen ist etwas schwierig. Genauso wie ihr auf der Erdoberfläche einen flachen Stadtplan verwenden könnt, wenn ihr nur ein paar Kilometer unterwegs seid, könnt ihr auch hier beim Wurmloch in der Umgebung jedes Punktes näherungsweise annehmen, dass der Raum ungekrümmt ist.
Eine Gleichung wie die Einstein-Gleichung macht deshalb keine Aussage darüber, ob der Raum global (oder mathematisch vornehm gesagt “topologisch”) einfach ist oder ein solches Wurmloch hat oder vielleicht das Bild oben nur ein Ausschnitt eines größeren Wurmlochs, der in einem noch komplizierteren Raumgebilde sitzt.
Wurmlöcher sind also durch die ART nicht ausgeschlossen – und bekanntlich ist ja alles, was nicht verboten ist, erst mal erlaubt.
Der Eingang eines Wurmlochs ist kugelförmig
Nehmen wir mal an, wir hätten ein Wurmloch irgendwo im All gefunden. Im Bild oben ist das Wurmloch ja wie ein Trichter; der Bereich, wo das Wurmloch anfängt, ist also kreisförmig. Deshalb wird oft angenommen, dass der Eingang in ein Wurmloch auch tatsächlich kreisförmig wäre – vielleicht kennt ihr ja das Sternentor aus dem film oder der Serie “Stargate” (hier aus Copyright-Gründen nur eine Zeichnung):
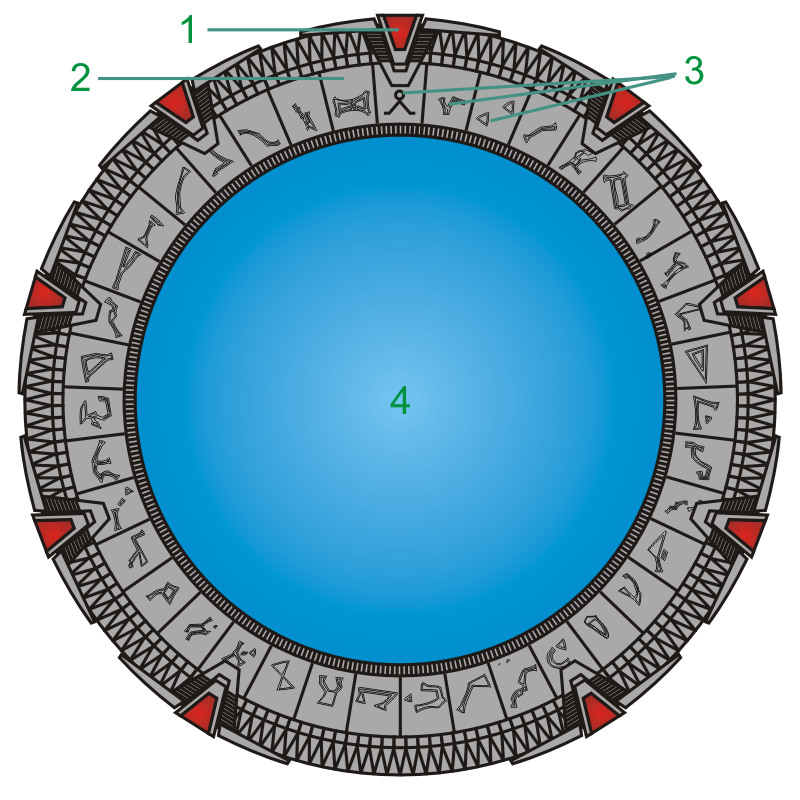
Von Stefan-Xp – Eigenes Werk, CC BY-SA 3.0, Link
Wenn ihr euch das Bild oben nochmal anschaut, seht ihr aber, dass es egal ist, aus welcher Richtung (innerhalb der blauen Fläche) ihr euch dem Wurmloch nähert, der Trichter sieht immer gleich aus. Und da das Bild eine Dimension unterschlägt, ist der “Eingang” zu einem Wurmloch also nicht kreis- sondern kugelförmig und sieht aus allen Richtungen gleich aus. (Das Wurmloch aus der Serie Deep Space 9 passt da schon besser, es ist im wesentlichen kugelförmig, allerdings von einem rotierenden Ring umgeben.)
Noch etwas anderes seht ihr oben auf dem Bild: der Eingang eines Wurmlochs kann vollkommen graduell sein, so dass ihr ganz gemütlich durchfliegen könnt (naja, von der exotischen Materie mal abgesehen, die kommt gleich.) Es ist denkbar, dass der Eingang zu einem Wurmloch sich im Inneren eines Schwarzen Lochs befindet – dann hat man erst den Rand des Schwarzen Lochs (den “Ereignishorizont”) und würde dann von dort aus in das Wurmloch gelangen. Das ist die Idee beim Wurmloch aus Stargate – der Ereignishorizont müsste aber wie gesagt kugelförmig sein, nicht flach und kreisförmig.
Durch Wurmlöcher kann man (vielleicht) durchgucken
Schaut wieder auf das Bild mit dem Trichter ganz oben und stellt euch einen Lichtstrahl vor, der auf das Wurmloch zufliegt. Der würde auf einer Seite in das Wurmloch hineinfliegen und auf der anderen wieder herauskommen – Licht breitet sich geradlinig auf, aber wenn der Raum gekrümmt ist, ist geradlinig nicht immer ganz gerade. Licht kann also aus dem Wurmloch herauskommen. (es sei denn, da ist weiter außen ein Ereignishorizont, weil das Wurmloch innerhalb eines Schwarzen Lochs ist, aber das ist nicht notwendig.) Deshalb kann man prinzipiell durch ein Wurmloch durchgucken. So etwa würde es aussehen, wenn ein Wurmloch von einer deutschen Stadt in eine Wüste führen würde (das Programm, mit dem das gemacht wurde, ist übrigens frei verfügbar):

Von CorvinZahn – Galerie von Tempolimit Lichtgeschwindigkeit (self-made, panorama of the dunes: Philippe E. Hurbain), CC BY-SA 2.5, Link
Die seltsamen Ringe kommen daher, dass das Licht ja auch schräg auf den “Trichter” treffen kann. Dann windet es sich ein paar mal um den Trichter herum, bevor es auf der anderen Seite wieder herauskommt, und entsprechend verzerrt sieht das Ergebnis aus. (Das ist ähnlich zu dem verzerrten Bild einer Akkretionsscheibe um ein Schwarzes Loch.)
Prinzipiell sollte man also durch ein Wurmloch durchgucken können, es sei denn, es gibt da ein Problem mit der exotischen Materie – zu der kommen wir jetzt.
Wurmlöcher brauchen exotische Materie
Wurmlöcher sind, wie oben erklärt, in der ART prinzipiell erlaubt. Aber damit es sie wirklich geben kann, muss man natürlich den Raum auch in die passende Form bringen, in diesem Fall eben in die Trichterform des Wurmlochs. Und dieser Trichter im Raum soll auch noch stabil sein, sich also mit der Zeit nicht ändern. Tja, wenn ihr das in die Gleichungen der ART einsetzt und dann ausrechnet, wie Materie verteilt sein müsste, um so ein Wurmloch zu erzeugen, dann gibt es da ein Problem: Stellt euch wieder vor, ihr würdet Licht auf das Wurmloch strahlen. Die Lichtstrahlen laufen dann zusammen, passieren das Wurmloch und laufen dann wieder auseinander. Ein solches Auseinanderlaufen von Licht lassen die Gleichungen der ART eigentlich aber nicht zu – Lichtstrahlen laufen entweder parallel oder sie laufen aufeinander zu, wenn Materie da ist, die den Raum krümmt. (So wie bei der berühmten Lichtablenkung bei der Sonnenfinsternis 1919.)
Damit Lichtstrahlen auseinanderlaufen können, braucht man etwas, das den Raum anders krümmt, als es normale Materie tut. So etwas gibt es leider nicht – aber zumindest theoretisch wäre es denkbar. Man bräuchte dazu ein Material, das unter extremer Zugspannung stehen kann (so wie ein gedehntes Gummiband), aber ohne dass jemand tatsächlich daran zieht. (Manchmal liest man auch, dass man Material braucht, das eine negative Energiedichte hat – diese beiden Forderungen sind mehr oder weniger äquivalent.) In der ART ist es nämlich so, dass auch eine mechanische Spannung die Raumkrümmung beeinflusst – das ist beispielsweise bei der Entstehung von Schwarzen Löchern wichtig. Druckspannungen ziehen den Raum stärker zusammen, Zugspannungen dagegen weiten ihn sozusagen auf. Es ist kein Problem für eine Materieansammlung, unter Druckspannung zu stehen – dafür sorgt schon die Schwerkraft der Materie selbst. Aber Materie, die, wenn man sie auf einen Haufen schmeißt, Zugspannungen erzeugt, gibt es normalerweise nicht. Deswegen bezeichnet man so etwas als “exotische Materie”.
Theoretisch ist so etwas aber denkbar. (Negative Energiedichten gibt es beispielsweise in der Quantentheorie beim Casimir-Effekt.) Wenn man solche Materie hätte, dann ließe sich mit ihr tatsächlich ein stabiles Wurmloch offenhalten. Ohne exotische Materie verdammen dagegen die Gleichungen der ART jedes Wurmloch dazu, zu kollabieren, bevor irgendetwas es durchquert hat. Und bisher gibt es leider keine Hinweise darauf, dass es so eine exotische Materie gibt. (Achtung: Manchmal werden auch andere Phänomene als “Exotische Materie” bezeichnet, beispielsweise Materie, die bottom-Quarks enthält, das ist hier aber nicht gemeint.)
Um das Wurmloch offenzuhalten, muss man also exotische Materie passend anordnen, beispielsweise im “Hals” des Wurmlochs (an der engsten Stelle). Das bedeutet natürlich auch, dass man beim Durchfliegen des Wurmlochs durch die exotische Materie fliegen muss – ob das überhaupt möglich ist, ist unklar, da wir ja nicht wissen, wie exotische Materie genau funktioniert. Das gleiche gilt auch für Licht, das durchs Wurmloch fliegt – auch das wird möglicherweise von der exotischen Materie beeinflusst. Theoretisch kann man zwar auch Wurmlöcher konstruieren, bei denen es Bereiche ohne exotische Materie gibt, durch die man von einer Seite zur anderen fliegen kann (dazu werden die Seiten des Wurmlochs quasi abgeflacht), aber das sind schon sehr spezielle Lösungen; zumindest auf natürlichem Weg kann so etwas nicht entstehen. (In der science fiction könnt ihr aber natürlich so ein Wurmloch verwenden.)
Wurmlöcher können nicht erzeugt werden
Nehmen wir also ganz optimistisch an, wir hätten irgendwo exotische Materie gefunden. Können wir jetzt ein Wurmloch nach Andromeda öffnen?
Leider nein. So etwa würde man sich die Entstehung eines Wurmlochs in unserem Bild ja vorstellen:

(Aus M.Bäker, “Isaac oder Die Entdeckung der Raumzeit”, Springer 2019, alle Rechte vorbehalten)
Und da wo im mittleren Bild das Fragezeichen steht, steckt das Problem: Unser Bild eines Wurmlochs stellt die Geometrie des Raums ja dadurch dar, dass wir den Raum in die dritte Dimension einbetten. Das macht die Sache für uns anschaulich, aber diese dritte, zusätzliche Dimension hat keine physikalische Bedeutung. Unsere Raumzeit ist – jedenfalls laut ART – nicht in etwas Höherdimensionales eingebettet. Und deswegen gibt es auch keine Möglichkeit zu sagen, dass sich die beiden “Beulen” in der Mitte “annähern” – in unserem Universum ist die eine Beule bei uns, die andere in der Andromeda-Galaxie, und es gibt da keinen Abstand, der sich irgendwie ändern könnte.
Darüber hinaus sagen die Gleichungen der ART ja (siehe oben), dass es der Raum immer lokal “flach” sein muss. Änderungen wie bei der Verbindung der beiden Hälften des Wurmlochs sind da nicht ohne weiteres möglich. (Prinzipiell gibt es da zwar die erweiterte Schwarzschildlösung, die eine Art “Wurmloch” enthält, dieses ist aber nicht passierbar und verbindet auch zwei unterschiedliche Raumzeiten, niemals zwei Bereiche derselben Raumzeit.)
Laut ART können Wurmlöcher also nicht entstehen. Das bedeutet aber nicht, dass es sie nicht geben kann – sie könnten entweder schon direkt beim Urknall entstanden sein (wenn eh die ganze Raumzeit entsteht, dann kann sie auch mit ner komplizierten Form entstehen) oder sie könnten durch Effekte zustande kommen, die über die ART hinausgehen, beispielsweise in der Quantengravitation. Wäre unsere Raumzeit tatsächlich in einen höherdimensionalen Raum (einen “Hyperraum”) eingebettet, dann wäre die Entstehung von Wurmlöchern schon denkbar – aber wie gesagt, im Rahmen der ART ist so etwas nicht vorgesehen. (Falls ihr gerade an die 11 Dimensionen der Stringtheorie denkt – die helfen in diesem Zusammenhang nicht weiter.)
Mit einem Wurmloch kann man eine Zeitmaschine bauen
Falls wir es aber geschafft haben, ein Wurmloch zu bauen, können wir damit noch viel coolere Sachen machen – beispielsweise eine Zeitmaschine bauen. Stellt euch vor, ihr habt ein Wurmloch mit den beiden Enden, die anfangs dicht benachbart sind. Ihr positioniert an jedem Ende des Wurmlochs eine Uhr (die ist nicht wirklich wichtig, soll nur veranschaulichen, was hier passiert) und schiebt dann ein Ende des Wurmlochs mit hoher Geschwindigkeit nach Alpha Centauri und wieder zurück zur Erde.Dann zeigt die Uhr des Wurmlochs, das die Rundreise gemacht hat, deutlich weniger Zeit an als die, die bei der Erde geblieben ist. Das ist das berühmte Zwillingsparadoxon (an dem nichts paradox ist). Hier ein Raumzeit-Diagramm der beiden Wurmlöcher:
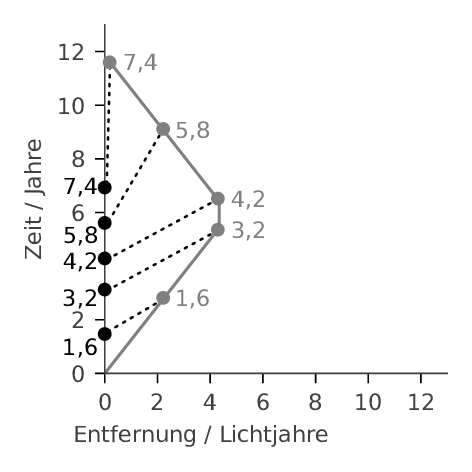
(Aus M.Bäker, “Isaac oder Die Entdeckung der Raumzeit”, Springer 2019, alle Rechte vorbehalten)
Für das bewegte Ende des Wurmlochs sind also 7,4 Jahre vergangen, für das andere dagegen vergehen knapp 12 Jahre.
Nehmen wir der Einfachheit halber an, der Weg durch das Wurmloch braucht keine Zeit. Ihr könnt jetzt oben im Bild in das Ende des Wurmlochs fliegen, das die Rundreise gemacht hat. Dann kommt ihr am anderen Ende des Wurmlochs wieder heraus, bei einer Zeit von 7,4Jahren, also deutlich in der Vergangenheit. So könnt ihr also problemlos Zeitreisen machen – vorausgesetzt, ihr findet einen Weg, Wurmlochenden auf nahezu Lichtgeschwindigkeit zu beschleunigen, aber wenn wir schon exotische Materie und all sowas haben, ist das dann auch nicht mehr viel verlangt.
Fazit: Science oder Fiction?
Wurmlöcher sind also zumindest theoretisch denkbar. Manchmal wird gesagt, dass sie eine Vorhersage der ART sind, das ist aber ziemlich übertrieben: Als Vorhersagen der ART können wir Phänomene wie Schwarze Löcher oder Gravitationswellen oder die Expansion des Universums ansehen – das sind Phänomene, die direkt aus den Gleichungen der ART folgen, ohne dass man zusätzliche Annahmen braucht. Wenn man hinreichend viel Materie anhäuft, muss sich ein Schwarzes Loch bilden, wenn man Objekte sich umkreisen lässt, müssen Gravitationswellen entstehen, wenn man ein Universum mit Materie drin hat, muss dieses entweder expandieren oder kollabieren (es sei denn, man wählt den genau passenden Wert der kosmologischen Konstante). Es gibt dagegen keine Situation, bei der laut ART ein Wurmloch entstehen muss (Hinweis für die Spitzfindigen: Ich rede nur von passierbaren Wurmlöchern, die erweiterte Schwarzschildlösung ist nicht gemeint). Mehr noch, damit es ein passierbares Wurmloch geben kann, brauchen wir erstens exotische Materie um es offenzuhalten und zweitens muss es irgendwoher kommen – und dieses irgendwoher ist eben nicht durch die ART abgedeckt.
Wurmlöcher sind also zwar mit der ART unter gewissen Bedingungen vereinbar, sie sind aber keine Vorhersage der ART. Ob es exotische Materie geben kann ist mehr als fraglich, ob Wurmlöcher überhaupt entstehen können, ebenso. Man kann deshalb durchaus berechtigte Zweifel anmelden, ob eine wissenschaftliche Untersuchung, wie man Wurmlöcher entdecken kann, mehr ist als “Science Fiction mit Gleichungen”, wie Sabine Hossenfelder es nennt:
The criteria for what counts as “theoretically possible” in the foundations of physics today are so weak that writing papers about observing these theoretical possibilities is just wasting everybody’s time. It’s science fiction with equations.
— Sabine Hossenfelder (@skdh) November 13, 2019
Meiner Ansicht nach sind Wurmlöcher im Moment eher “fiction” als “science” – sie sind theoretisch denkbar, aber das sind Einhörner auch. Dafür, dass es sie gibt, gibt es keinerlei Hinweise. (Cool wäre es natürlich trotzdem…)






Kommentare (53)