Noch ein Planet
Denn eigentlich wollen wir ja etwas über mögliche zusätzliche Planeten erfahren. Das bedeutet, wir müssen noch einmal jede Menge Möglichkeiten durchprobieren; nämlich alle die Bahnen, bei denen wir wissen möchten, ob dort noch ein weiterer Planet existieren könnte oder nicht.
Da wir keine Ahnung haben, wie die Bahn so eines Planeten aussieht (bzw. ob er überhaupt existiert) müssen genaugenommen alle 7 Bahnelemente alle möglichen Kombinationen durchlaufen. Zusammen mit den möglichen Parametern für den schon bekannten Planeten kommt da eine große Menge an Anfangszuständen zusammen. Natürlich könnte man alle Möglichkeiten durchrechnen – man braucht nur ausreichend Computerpower. Aber in der Praxis läuft das dann doch meistens anders ab.
Für den schon bekannten Planet wählt man für die ersten Untersuchungen die wahrscheinlichsten Paramter aus. Auch die Paramter für den möglichen zusätzlichen Planeten (meistens “Testkörper” bzw. “test particle” genannt) lassen sich einschränken. Im Allgemeinen betrachtet man die Testkörper als masselos (im Vergleich zum Stern und dem großen Planeten ist ein Körper wie die z.B. Erde in erster Näherung tatsächlich “masselos” und das Modell gültig). Damit fällt schon mal ein Paramter weg. Dann bringt es natürlich auch nichts, alle Werte für die große Halbachse (als den Abstand des Testkörpers vom Stern) auszuprobieren. Aber einer gewissen Entfernung vom Stern bzw. vom großen Planeten ist deren Einfluss auf die Stabilität sowieso gering. Aus dynamischer Sicht muss der Einfluss von mindestens 2 Objekten “spürbar” sein. Wenn der große Planete und Testkörper zuweit voneinander entfernt sind, dann bewegen sich beide unabhängig voneinander und eine Stabilitätsanalyse macht wenig Sinn.
Im Normalfall wählt man daher für den Testkörper ein “interessantes” Intervall für die Werte der großen Halbachse “a” (z.B. den Bereich der habitablen Zone – der Bereich um einen Stern, in dem theoretisch Leben auf der Oberfläche eines Planeten existieren könnte) und dann noch jeweils ein passendes Intervall für die Werte von Exzentrizität “e” und Inklination “i” (also der Neigung der Bahn des Testkörpers gegenüber des großen Planeten).
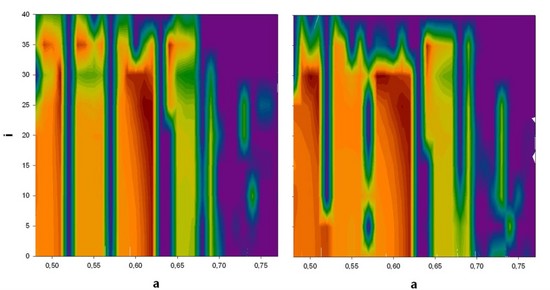
In diesem Netz aus Anfangsbedingungen (a,e) bzw (a,i) wird nun für jeden Gitterpunkt die Stabilität der Bahn unter dem gravitativen Einfluss des großen Planeten berechnet. Das Ergebniss kann dann z.B. so aussehen:
Hier ist auf der x-Achse die große Halbachse des Testkörpers aufgetragen (der Bereich entspricht der habitablen Zone); auf der y-Achse die Inklination. Die Farbe zeigt an, ob der jeweilige Bereich stabil ist oder nicht (rot/orange/gelb zeigt Stabilität an; grün/blau/violett Chaos). Es handelt sich bei diesem Beispiel übrigens um das Planetensystem um HD 41004 A – einen Doppelstern. Die beiden Bilder zeigen die Stabilität je nachdem ob man den zweiten Stern berücksichtigt (links) oder ignoriert (rechts).
Am Streifenmuster aus abwechselnd chaotischen und stabilen Bereichen erkennt man übrigens wunderbar den Einfluss der Resonanzen auf die Stabilität. Stabile Bereiche werden dort, wo Resonanzen der mittleren Bewegung herrschen, durch chaotische Regionen unterbrochen.
Um eine genauere Analyse der Resonanzen vorzunehmen reichen die obigen Einschränkungen übrigens nicht aus. Bei den Resonanzen der mittleren Bewegung kommt es sehr auf die relative Position der beteiligten Planeten an. Deswegen muss man hier auch noch die Werte für die mittlere Anomalie variieren bzw. die Werte für die beiden anderen Winkel, wenn man auch die säkularen Resonanzen untersuchen will.
Qual der Wahl
Die richtigen Parameter für die Analysen zu wählen kann also oft ganz schön knifflig sein. Die Wahl hängt stark davon ab, was man eigentlich untersuchen will. Und selbst wenn man sich dann mal für etwas entschieden hat, das vernünftig scheint, kann es immer noch Probleme geben. Es kam schon öfter vor, dass neue Beobachtungen die publizierten Werte eines Exoplaneten völlig über den Haufen geschmissen haben. Statt etwa 5facher Jupitermasse hat ein Planet dann plötzlich nur noch die 2fache Masse. Statt einer exzentrischen Bahn ist die Bahn dann plötzlich kreisförmig. Statt einem bekannten Planeten befinden sich plötzlich 2 Planeten im System.











Kommentare (5)