Ich habe sicher schon das eine oder andere Mal erwähnt, dass die Astronomie eine ziemlich großartige Wissenschaft ist. Das ist sie nicht nur, weil sie sich mit ziemlich großartigen Themen und Dingen beschäftigt. Sondern auch aufgrund der Art und Weise wie man in der Astronomie das Universum untersucht. Astronomen können nur schauen. Sie können nichts von all den anderen Dingen machen, die in anderen Wissenschaften möglich sind. Astronomen können nur schauen, denn ihre Untersuchungsobjekte sind unvorstellbar weit entfernt. Ihnen bleiben nur ein paar Photonen, die aus dem fernen All auf ihre Teleskope treffen und daraus müssen sie alles ableiten, was sie wissen wollen. Erstaunlicherweise funktioniert das ziemlich gut! Und zwar nicht nur bei Himmelskörpern, die man auch tatsächlich sehen kann, sondern sogar bei denen, die nicht sichtbar sind. Den extrasolaren Planeten zum Beispiel.
Von den knapp 1000 bekannten extrasolaren Planeten haben wir nur eine Handvoll direkt gesehen. Denn so gut wie immer wird der kleine Planet vom viel helleren Stern komplett überstrahlt. Nur in ein paar Ausnahmefällen gelang es, das vom Planeten reflektierte Sternenlicht direkt im Teleskop zu beobachten. Aber auch wenn man die Planeten nicht direkt gesehen hat, hat man doch erstaunlich viele Informationen über sie gewinnen können. Die verschiedenen Entdeckungsmethoden habe ich in meiner Serie “Die wunderbare Welt der Exoplaneten” erklärt. Eine davon ist die Transitmethode. Mit ihren werden mittlerweile die meisten Planeten gefunden. Man beobachtet dabei einen Stern und hofft, dass ein Planet an ihm vorüber zieht. Dann blockiert er ein wenig vom Licht des Sterns und der wird ein bisschen dunkler. Natürlich klappt das nur, wenn man genau im richtigen Winkel auf das Planetensystem blickt und man braucht schon ein wenig Glück, um so Planeten zu finden. Aber da draußen sind jede Menge Sterne und wenn man genug davon betrachtet, dann findet man auch etwas. Mit dieser Methode kann man herausfinden, wie groß der Planet ist, auch wenn man ihn gar nicht sieht. Denn natürlich wird der Stern um so dunkler, je größer der Planet ist. Man kann auch herausfinden, wie schnell er sich bewegt (je schneller, desto kürzer ist die Verdunkelungsphase) und damit auf den Abstand zum Stern schließen (dabei hilft das dritte Keplersche Gesetz). Aber man weiß nichts über die Masse des Planeten. Und auch nichts darüber, wie “schief” die Bahn des Planeten im Raum liegt.
Die Masse ist relativ leicht herauszufinden. Dafür kann man eine andere Methode benutzen, die “Radialgeschwindigkeitsmethode”. Hier misst man nicht die Helligkeit des Sternenlichts, sondern seine Bewegung. Die Gravitationskraft des Planeten lässt den Stern ein klein wenig hin und her wackeln. Mal wackelt er auf uns zu und dann wieder von uns weg. Das kann man an einer Verschiebung der Spektrallinien erkennen (wie das genau funktioniert habe ich hier erklärt). Mal sind sie zum roten Ende des Lichtspektrums verschoben, mal zum blauen Ende.
Man kann im Prinzip bei jedem Stern mit einem Planeten auch eine entsprechende Verschiebung der Spektrallinien messen (vorausgesetzt die Instrumente sind genau genug), aber nicht bei jedem Stern mit einem Planeten sieht man auch einen Transit, weil das ja vom Blickwinkel abhängt. Aber wenn man einen Transit sieht, dann kann man auch nach einer Verschiebung der Spektrallinien suchen. Damit kann man dann nicht nur die Masse des entdeckten Planeten bestimmen, sondern auch noch die Neigung seiner Bahn. Das geht mit dem Rossiter-McLaughlin-Effekt und der zeigt ganz wunderbar, wie kreativ die Astronomen werden können, wenn sie etwas über Dinge herausfinden wollen, die sie nicht sehen können.
Der Effekt der Radialgeschwindigkeit ist nicht schwer zu verstehen. Im gleichen Rhythmus in der sich der Planet um den Stern bewegt, wackelt auch der Stern. Misst man also die Geschwindigkeit, mit er auf uns zu kommt bzw. sich von uns entfernt, dann wird sie sich periodisch ändern. Und je stärker die Änderung ist, desto schwerer ist der Planet. Das hat aber noch nichts mit dem Rossiter-McLaughlin-Effekt zu tun. Um den zu finden, muss man ganz genau schauen. Man muss den Stern genau in dem Moment beobachten, in dem der Planet vor ihm vorüber zieht.
Jeder Stern rotiert. Blicken wir genau von “vorne” auf einen rotierenden Stern, dann dreht sich eine Hälfte auf uns zu, die andere von uns weg. Ganz unabhängig von der durch den Planeten verursachten Wackelei kann man auch diese Bewegung des Sterns in den Spektrallinien sehen. Die Rotation sorgt dafür, dass das Licht von der einen Seite des Sterns ein bisschen Richtung rot verschoben ist, die andere ein bisschen Richtung blau. Man bekommt also nicht nur eine scharfe Spektrallinie, sondern eine, die ein wenig hin und her wackelt und daher bei längerer Belichtung verschmiert und damit verbreitert wird. Je schneller sich der Stern dreht, desto größer ist auch die Verbreiterung der Linien. Aber wenn nun auch noch ein Planet mit ins Spiel kommt, wird die Sache wirklich interessant!
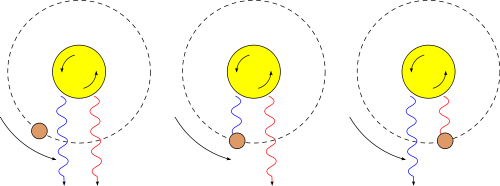
Das Bild oben zeight, was passiert. Während der Planet vor dem Stern vorüber zieht, blockiert er zuerst das Licht auf der einen Seite des Sterns. Wenn das zum Beispiel gerade die Seite ist, die sich auf uns zu dreht, dann wird dieses Richtung blau verschobene Licht kurzfristig blockiert und wir sehen nur rotverschobenes Licht von der anderen Seite. Bewegt sich der Planet weiter, dann sehen wir das blauverschobene Licht, aber das rotverschobene wird nun blockiert. Der Effekt ist meistens nicht sehr groß, kann aber gemessen werden. Wie genau die gemessene Radialgeschwindigkeitsänderung aussieht, hängt davon ab, wie groß der Winkel zwischen der Bahnebene des Planeten und der Rotationsachse des Sterns ist. Das zeigen diese Diagramme recht gut:
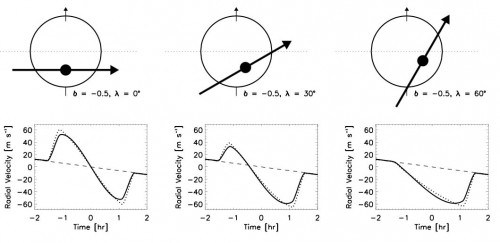
Links sieht man die “normale” Situation. Die Rotationsachse des Sterns steht senkrecht auf der Bahnebene des Planeten. So ist es auch bei den meisten Planeten in unserem Sonnensystem. Das Bild in der zweiten Reihe zeigt, wie sich hier die Radialgeschwindigkeit ändert. Die Bilder in der Mitte und ganz rechts zeigen nun Planeten, deren Bahn ein wenig “schief” ist. Dadurch verdecken sie die rotverschobene bzw. blauverschobene Seite des Sterns nicht mehr symmetrisch und auch die Radialgeschwindigkeitskurve wird asymmetrisch.
Der Rossiter-McLaughlin-Effekt erlaubt es, die Neigung der Bahnebene von extrasolaren Planeten zu bestimmen. Das ist aus mehreren Gründen wichtig. Man kann so verschiedene Migrationsmodelle überprüfen. Viele Planeten bleiben nach ihrer Entstehung nicht dort, wo sie sind, sondern bewegen sich durch das System. Es gibt theoretisch verschiedene Möglichkeiten, wie sie das tun können und sie unterscheiden sich unter anderem durch die Neigung der Bahn, die die Planeten nach der Migration haben. Man lernt mit dem Rossiter-McLaughlin-Effekt also nicht nur die Planeten selbst ein wenig besser kennen, sondern kann auch ihre Enstehung genauer verstehen. Und abgesehen davon zeigt er ziemlich beeindruckend, wie gut die Astronomen darin geworden sind, dem Licht auch noch das letzte bisschen Information zu entreißen!











Kommentare (29)