 Dieser Artikel ist Teil einer fortlaufenden Besprechung des Buchs “Wenn Gott würfelt: oder Wie der Zufall unser Leben bestimmt” (im Original: “The Drunkard’s Walk: How Randomness Rules Our Lives”) von Leonard Mlodinow. Jeder Artikel dieser Serie beschäftigt sich mit einem anderen Kapitel des Buchs. Eine Übersicht über alle bisher erschienen Artikel findet man hier.
Dieser Artikel ist Teil einer fortlaufenden Besprechung des Buchs “Wenn Gott würfelt: oder Wie der Zufall unser Leben bestimmt” (im Original: “The Drunkard’s Walk: How Randomness Rules Our Lives”) von Leonard Mlodinow. Jeder Artikel dieser Serie beschäftigt sich mit einem anderen Kapitel des Buchs. Eine Übersicht über alle bisher erschienen Artikel findet man hier.
——————————————————-
Im ersten Kapitel des Buchs hat Mlodinow anschaulich dargelegt, wie sehr der Zufall unser Leben bestimmt und vor allem dort, wo wir nicht damit rechnen. Das zweite Kapitel hat sich mit den grundlegenden Regeln der Wahrscheinlichkeit beschäftigt. Im dritten Kapitel präsentiert Mlodinow das fiese Ziegenproblem, das unser Unverständnis der Wahrscheinlichkeit eindrucksvoll präsentiert.
Wenn wir mit den Wahrscheinlichkeiten klar kommen wollen, dann brauchen wir dazu die Mathematik. Nachdem (wie im letzten Kapitel des Buchs beschrieben) Gerolamo Cardano die ersten Grundlagen gelegt hat, erklärt Mlodinow im vierten Kapitel wie es weiter geht. Und zwar – vielleicht ein wenig überraschend – mit Galileo Galilei. Der wurde von seinem Mäzen, der offensichtlich ein großer Spieler war, gefragt, warum man beim Würfeln mit drei Würfeln ein klein wenig öfter insgesamt 10 Punkte würfelt als 9. Denn eigentlich sollte es gleich wahrscheinlich sein: Es gibt in beiden Fällen sechs Arten, wie man aus drei Zahlen zwischen 1 und 6 die Summen 9 oder 10 konstruieren kann: (6+2+1), (5+3+1), (5+2+2), (4+4+1), (4+3+2) und (3+3+3) bzw. (6+3+1), (6+2+2), (5+4+1), (5+3+2), (4+4+2) und (4+3+3).
Galileo Galilei hatte zwar keine große Lust sich mit den trivialen Würfelproblemen seines Geldgebers zu beschäftigen. Aber weil es der Geldgeber war, blieb ihm kaum eine andere Wahl. Und er fand schnell die Lösung. Denn natürlich sind die verschiedenen Möglichkeiten nicht gleichwertig. Zum Beispiel kann man die Kombination (6+3+1) auf sechs verschiedene Arten würfeln: 631, 613, 316, 361, 136 und 163. Es gibt dagegen nur eine Möglichkeit (3+3+3) zu würfeln. Wenn man das alles aufdröselt landet man bei 27 Möglichkeiten, insgesamt 10 Punkte zu würfeln und 25 für eine 9. Galileo hatte eine weitere wichtige Regel der Wahrscheinlichkeitsrechnung aufgestellt: Die Wahrscheinlichkeit eines Ereignisses hängt davon ab, auf wie viele unterschiedliche Arten es passieren kann.
Aber wie viele Arten es genau gibt, ist oft ziemlich knifflig zu berechnen. Wie man das aber trotzdem den Umständen entsprechend recht einfach tun kann, hat ein wenig später der große französische Mathematiker Blaise Pascal herausgefunden. Pascal wurde von einem Adligen gebeten, folgendes Problem zu lösen: Angenommen, zwei Spieler spielen ein Spiel und beide haben gleich gute Chancen zu gewinnen. Der Sieger ist der, der zuerst eine gewissen Anzahl von Punkten erreicht hat. Dann aber muss das Spiel abgebrochen werden, während einer der Spieler gerade in Führung liegt. Wie soll man das Preisgeld gerecht aufteilen? Oder anders gesagt: Wie groß ist die Wahrscheinlichkeit, dass der hinten liegende Spieler doch noch gewinnt.
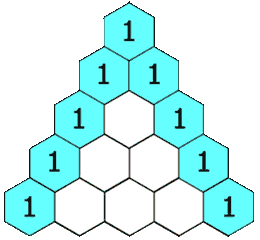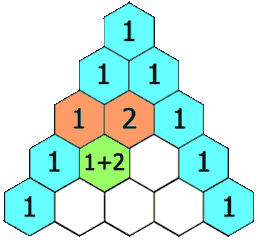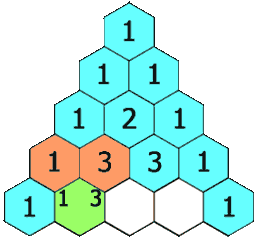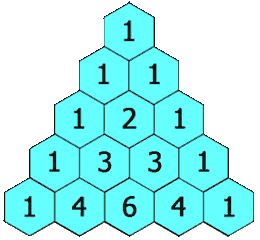
Um dieses Problem zu lösen musste Pascal herausfinden, auf wie viele Arten das Spiel von jedem Spieler gewonnen bzw. verloren werden kann. Die Berechnung dieser Möglichkeiten artet schnell in sehr große Zahlen aus – aber Pascal fand einen mathematischen Trick, der diese Berechnung anschaulich macht. Wir nennen diesen Trick heute das Pascalsche Dreieck (obwohl andere früher und unabhängig zu dem gleichen Ergebnis kamen):
Die Animation zeigt, wie man so ein Dreieck konstruiert. Man beginnt mit einer “1” an der Spitze. Die Zahlen der nächsten Reihe werden aus den Zahlen (bzw. der Zahl) darüber gebildet. Jede Zahl ist die Summe der beiden Zahlen direkt darüber. In der zweiten Zeile ist das die Summe aus der 1 und einer Null (weil dort keine Zahl steht). Die dritte Zeile wird genau so gebildet: (0+1=1), (1+1=2), (1+0=1). Und so weiter.
Die Zahlen im Dreieck geben nun genau an, wie viele Variationsmöglichkeiten eine Gruppe mit einer gewissen Zahl an Elementen hat. Stellen wir uns vor, wir haben 4 Freunde zu besuchen und wollen wissen, auf wie viele verschiedene Möglichkeiten wir diese 4 Freunde an unserem Tisch platzieren können. Dazu schauen wir uns die fünfte Reihe des Dreickes an (die erste Reihe ist eigentlich die nullte Reihe da die Zählung hier mit “0” beginnt). Die erste Zahl dort sagt uns, auf wie viele Arten wir 0 Gäste aus unseren 4 aussuchen können. Da gibt es logischerweise nur eine Möglichkeit: Nämlich keinen Gast auszuwählen. Die zweite Zahl sagt uns, wie viele Arten es gibt, einen Gast auszuwählen und das sind natürlich 4. Die dritte Zahl gibt ab, auf wie viele unterschiedliche Arten wir zwei Gäste aus der Gruppe von 4 auswählen können und das sind 6. Und so weiter: Wir können auf vier Arten drei Gäste auswählen und auf eine Art vier Gäste. Insgesamt gibt es 1+4+6+4+1=16 Möglichkeiten, die vier Gäste anzuordnen.
Das Pascalsche Dreieck ist in vielen Bereichen nützlich. Mlodinow bringt ein Beispiel aus der Wirtschaft. Angenommen man hat ein neues Produkt, das im Prinzip 50 Prozent der Menschen gefällt und 50 Prozent nicht. Und weiter angenommen, man präsentiert das Produkt während der Entwicklung einer kleinen Gruppe von 6 Leute um herauszufinden wie gut es ankommt. Wie genau wird die Meinung der Gruppe mit der Meinung der Gesamtbevölkerung übereinstimmen? Oder anders gesagt: Wie viele Wege gibt es, die 6 Leute in Gruppen unterschiedlicher Meinung aufzuspalten? Dazu schauen wir die entsprechende Reihe im Pascalschen Dreieck an in der die Zahlen 1, 6, 15, 20, 15, 6, 1 stehen. Insgesamt sind das 64 Möglichkeiten. Zwei von diesen 64 Fällen entsprechen einer einstimmigen Meinung: Allen gefällt es oder alle finden es doof. 12 (6+6) der 64 Fälle entsprechen Situationen in der eine Person das Produkt doof findet und die anderen toll bzw. umgekehrt. 30 (15+15) Fälle entsprechen einer 2 zu 4 bzw. einer 4 zu 2 Entscheidung gegen das Produkt. Und nur 20 der 64 Fälle geben die Realität tatsächlich wieder und entsprechen einer 3 zu 3 Aufteilung der Meinungen. In 20 von 64 Fällen wird also die kleine Gruppe die Meinung der Bevölkerung repräsentieren. In 44 von 64 Fällen wird sie dagegen davon abweichen! Das muss man bei allen weiteren Analysen berücksichtigen!
Eine weitere wichtige Idee die Pascal entwickelt hat, ist die des Erwartungswertes. Nicht nur spielt die Wahrscheinlichkeit eine Rolle wenn man den Ausgang eines Ereignisses beurteilen will: Man muss auch berücksichtigen, was der jeweilige Ausgang für Folgen hat. Pascal, der mittlerweile die Mathematik weitesgehend aufgegeben und sich der Religion zugewandt hat, dachte über Religion nach. Lohnt es sich, gläubig zu sein, oder nicht? Die Wahrscheinlichkeit dass Gott existiert beträgt 50 Prozent, sagte Pascal. Entweder es gibt ihn, oder nicht. Aber dann muss man auch die Konsequenzen berücksichtigen. Existiert Gott, dann ist der Lohn eines gläubigen Lebens die ewige Glückseligkeit; er ist also unendlich groß. Existiert Gott dagegen nicht, verliert man nur die Zeit, die man für seinen Glauben aufgewendet hat. Pascal schlug nun vor, die zu erwartenden Gewinne und Verluste mit den jeweiligen Wahrscheinlichkeiten zu multiplizieren um zu sehen, welcher Weg profitabler ist. Der durchschnittliche Gewinn für ein gläubiges Leben ist hier also eine unendlich große Zahl (die ewige Glückseligkeit) multipliziert mit 0,5 (den 50 Prozent für die Wahrscheinlichkeit der Existenz Gottes) minus einer kleinen Zahl (dem, was man durch das gläubige Leben verliert) multipliziert mit 0,5 (den 50 Prozent für die Wahrscheinlichkeit der Nicht-Existenz Gottes). Insgesamt also eine halbe Unendlichkeit minus der Hälfte einer endlich großen Zahl was in Summe immer noch unendlich groß ist. Der zu erwartenden Gewinn eines gläubigen Lebens ist also unendlich groß und deswegen sei es nur logisch, an Gott zu glauben.
Diese “Pascalsche Wette” ist allerdings ein Zirkelschluss. Sie funktioniert nur, wenn man schon an einen ganz konkreten Gott mit konkreten Eigenschaften glaubt. Denn was nützt es, wenn man sein Leben lang ein Leben nach den Regeln des christlichen Gottes führt, nur um nach dem Tod zu merken, dass der wahre Gott der Gott einer ganz anderen Religion ist, den man mit seinem christlichen Leben erst Recht wütend gemacht hat… Und natürlich ist auch die Prämisse unlogisch, dass die Wahrscheinlichkeit der Existenz Gottes 50 Prozent beträgt. Nur weil man sagen kann: “Entweder etwas ist so oder es ist nicht so”, folgt daraus noch nicht das beides gleich wahrscheinlich ist. Entweder mir fällt morgen ein Meteorit auf den Kopf wenn ich aus dem Haus gehen oder es fällt mir kein Meteorit auf den Kopf. Aber deswegen ist das eine nicht genau so wahrscheinlich wie das andere.
Aber trotz der Unlogik der Pascalschen Wette ist das Konzept des Erwartungswertes äußerst nützlich. Wir verstehen es allerdings genauso wenig intuitiv wie den Rest der Wahrscheinlichkeit. Mlodinow beschreibt folgendes Spiel: Die Regierung von Kalifornien bietet jedem Bürger an, einen Dollar zu bezahlen. Ein Bürger bekommt dafür jede Menge Geld geschenkt. Die allermeisten bekommen nichts. Und eine Person muss eines gewaltsamen Tods sterben. Würde man bei so einem Spiel mitmachen? Die Bürger von Kalifornien tun es jedenfalls mit Begeisterung. Sie nehmen an der Staatslotterie teil, obwohl der Erwartungswert ihnen sagt, dass sie mit an Sicherheit grenzender Wahrscheinlichkeit ihr Geld verlieren werden. Und die Statistik zeigt, dass pro Ziehung zumindest eine Person einen tödlichen Verkehrsunfall auf dem Weg zur Lotterie-Annahmestelle haben wird.
Das hinterhältige an den Wahrscheinlichkeiten ist ja, dass sie nichts über den Einzelfall aussagen können. Sie machen nur dann Sinn, wenn man ausreichend viele Fälle beobachtet. Und darum geht es im nächsten Kapitel!












Kommentare (120)