Wo stecken die Asteroiden
Wo sonst, wenn nicht in Regensburg? Hier verstarb im Jahr 1630 der große Astronom Johannes Kepler. Sein 1609 veröffentlichtes Buch trägt nicht umsonst den Titel “Astronomia Nova”. Er hat tatsächlich eine völlig neue Astronomie geschaffen und sie, zwar nicht alleine aber doch maßgeblich, zu der Wissenschaft gemacht, die sie heute ist. Kepler war der erste, der die Bewegung der Himmelskörper quantitativ mit mathematischen Regeln beschreiben könnte. Der erste zumindest, dessen Regeln auch ausreichend gut mit den Beobachtungsdaten übereinstimmten.
Keplers große Leistung war nicht die Erkenntnis, dass sich die Planeten um die Sonne bewegen. Das haben vor ihm schon viele andere vermutet und durch Beobachtungen auch untermauert. Aber seine Vorgänger und Zeitgenossen waren immer davon überzeugt, dass diese Bewegung entlang kreisförmiger Bahnen stattfinden muss. Für diese Überzeugung gab es keine zwingende Grundlage, sondern hauptsächlich philosophische und ästhetische Gründe. Der Kreis war eben die perfekte Form. Aber nur weil wir Menschen etwas als “perfekt” empfinden muss sich die Natur nicht daran halten.
In jahrelanger mathematischer Arbeit stellte Kepler fest, dass sich die Planeten auf elliptischen Bahnen bewegen und seine drei berühmten Gesetze quantifizieren diese Bewegung. Sie sagen uns, wie schnell sich die Planeten bewegen und wie die Form ihrer Bahn mit ihrer Geschwindigkeit zusammenhängt. Das war eine revolutionäre Leistung und wenn Kepler noch ein bisschen weiter gedacht hätte, hätte er noch vor Isaac Newton das Gravitationsgesetz finden können. In der Astronomia Nova steht er schon kurz davor, denn Zusammenhang zwischen Masse, Abstand und Gravitationskraft zu entdecken, ist aber die letzten logischen Schritte nicht mehr gegangen. Heute wissen wir, dass man aus Keplers Gesetzen die Gravitationsgleichung ableiten kann und das gilt natürlich auch umgekehrt.
Berechnet man mit Newtons Formel auf welcher Bahn sich zwei Himmelskörper gegenseitig umkreisen müssen, dann erhält man die Gleichung einer Ellipse (bzw. allgemein die Gleichung für Kegelschnitte). Allerdings nur, wenn es tatsächlich um zwei Himmelskörper geht. Sobald ein dritter Körper involviert ist, wird die Sache kompliziert. So kompliziert, dass es nicht mehr möglich ist, die Gleichungen zu lösen. Nicht nur praktisch, sondern auch theoretisch. Es gibt keine allgemeine Lösung, die die Bewegung von mehr als zwei Himmelskörpern für alle Zeiten angibt. Das liegt am Chaos und den wechselseitigen Störungen, die die Planeten aufeinander ausüben.
Jeder Himmelskörper beeinflusst jeden anderen Himmelskörper mit seiner Gravitationskraft und zwar umso stärker, je mehr Masse er hat. Die Sonne hat bei weitem die allergrößte Masse und den stärksten Einfluss. Daher kann man in erster Näherung all die anderen Einflüsse vernachlässigen und nur die Wechselwirkung zwischen Sonne und Planet betrachten. Und dann erhält man Keplers elliptische Bahnen als Lösung. Aber in der Realität spielen eben auch die kleinen Störungen der anderen Planeten eine Rolle und dann sind die Keplerschen Gesetze keine exakte Beschreibung mehr. Über lange Zeiträume hinweg betrachtet, verändern sich die elliptischen Keplerbahnen der Himmelskörper. Die Ellipsen werden größer und kleiner, mehr oder weniger elliptisch und wackeln im Raum hin und her.
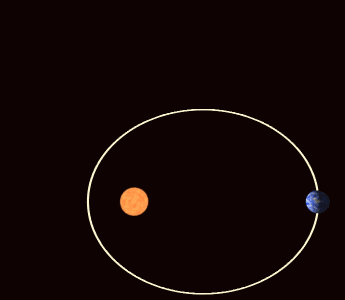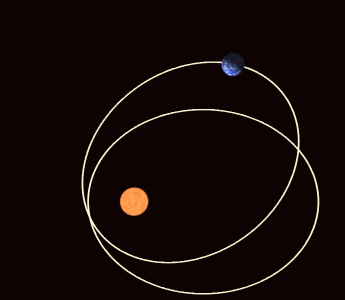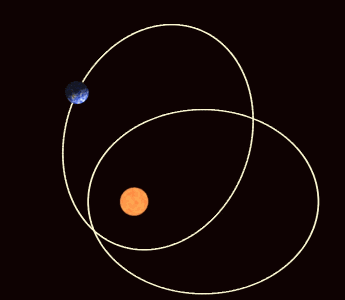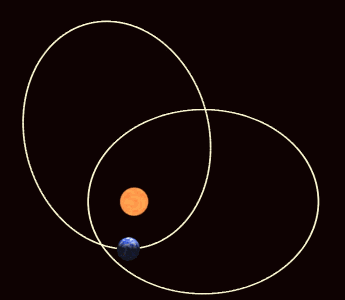
Die Keplerbahnen der Planeten verändern sich im Laufe der Zeit (Bild: WilloW CC-BY 3.0)
Und gerade wenn es um die Asteroiden geht, kann das dramatische Folgen haben. Gestern in der Oberpfalz haben wir den Asteroid Eros getroffen. Er gehört zu den erdnahen Asteroiden, einer Gruppe von Himmelskörpern die sich irgendwo zwischen den Bahnen von Mars und Venus aufhalten können. Die Bahnen der erdnahen Asteroiden sind nicht stabil; nach ein paar zehntausend bis hunderttausend Jahren stoßen sie mit einem Planeten zusammen, fallen in die Sonne oder werden aus dem Sonnensystem geworfen. Grund für die Instabilität sind die Störungen der anderen Planeten. Da die erdnahen Asteroiden immer wieder in die Nähe von Mars, Erde oder Venus kommen können, werden die von dort wirkenden Gravitationskräfte sehr stark und die Bahnen ebenso stark verändert. Langfristig können diese Asteroiden also nicht überleben.













Kommentare (11)