Nichts bewegt sich schneller als das Licht! Das ist eine der großen physikalischen Erkenntnisse des 20. Jahrhunderts. Aber unser Verständnis der Naturgesetze ist nicht für alle Ewigkeiten in Stein gemeißelt, sondern einem stetigen Prozess der Veränderung unterworfen. Je genauer wir die Natur betrachten, desto genauer wird auch unsere Beschreibung. Als Albert Einstein vor fast 100 Jahren intensiv über Gravitation nachdachte, fand er am Ende ein Modell, das die Realität ein klein wenig genauer beschrieb als die Gravitationstheorie von Newton. Und in 100 Jahren wird vielleicht jemand anderes zeigen können, dass man eine noch bessere Annäherung an die Natur als Einstein finden kann. Mit der Lichtgeschwindigkeit als Geschwindigkeitslimit könnte es vielleicht ähnlich sein. Gerade macht eine Arbeit des Physikers Robert Ehrlich die Runde in den Medien (“Six observations consistent with the electron neutrino being a tachyon with mass: m2νe=−0.11±0.016eV2”) in der nahegelegt wird, dass Neutrinos sich schneller als das Licht bewegen.
Ich sage sicherheitshalber gleich zu Beginn, worum es in diesem Artikel nicht gehen wird: Um überlichtschnelle Raumfahrt, Warp-Antriebe, freie Energie aus dem Nichts und ähnliche Grenzgebiete der Science-Fiction und Pseudowissenschaft. Es geht um Elementarteilchen und theoretische Physik – aber die Sache ist trotzdem äußerst interessant.

Albert Einstein (der die Lichtgeschwindigkeit als universales Geschwindigkeitslimit einführte) und Wolfgang Pauli (der die Existenz des Neutrinos vorhersagte). Bild: (c) CERN
Neutrinos sind sehr faszinierende Elementarteilchen. Sie wurden 1930 vorhergesagt und 1956 nachgewiesen. Sie interagieren so gut wie gar nicht mit normaler Materie (Neutrinos sind “dunkle Materie”, das heißt sie senden keine elektromagnetische Strahlung aus und absorbieren sie auch nicht sondern interagieren nur über die schwache Kernkraft mit dem Rest der Materie). Wir haben aber mittlerweile gelernt, sie trotzdem zu registrieren (siehe hier und hier) und diese Teilchen verraten uns viel darüber, was im Universum vor sich geht.
Eine der immer noch ungelösten Fragen bei diesem Thema ist die Masse der Neutrinos. Ursprünglich dachte man, sie hätte gar keine Ruhemasse; so wie zum Beispiel auch die Photonen des Lichts. Und als masselose Teilchen würden sich die Neutrinos dann auch mit Lichtgeschwindigkeit bewegen. Diverse Experimente und theoretische Überlegungen haben aber mittlerweile zu der Überzeugung geführt, dass sie doch eine sehr, sehr kleine Ruhemasse besitzen und daher auch ein klein wenig langsamer als das Licht sind. Der genaue Wert der Masse ist allerdings noch unbekannt.
Und hier kommt die Arbeit von Robert Ehrlich ins Spiel: Er behauptet, die Neutrinos hätten eine imaginäre Masse. Das klingt nicht nur ziemlich seltsam. Das ist auch ziemlich seltsam. Imaginäre Zahlen werden die meisten noch aus dem Schulunterricht kennen. Man hat sie eingeführt, um Gleichungen wie x² = -1 lösen zu können. Mit den “normalen” Zahlen geht das nicht, denn egal ob man eine positive oder eine negative Zahl mit sich selbst multipliziert; am Ende ist das Ergebnis immer positiv. Der Ausweg aus diesem Dilemma waren die imaginären Zahlen. Man hat einfach per Definition festgelegt, dass eine Zahl mit der Bezeichnung “i” existieren soll, die gleich der Wurzel aus -1 ist. Dann ist i² = -1 und die Lösung für die oben gestellte Gleichung lautet einfach x=i. Mit imaginären Zahlen kann man genau so rechnen wie mit normalen Zahlen und die moderne Mathematik bzw. Physik würde mittlerweile nicht mehr ohne diese Erweiterung des Zahlenraums auskommen. Aber eine Entsprechung in der realen Welt haben die imaginären Zahlen nicht. Was also soll es dann bedeuten, wenn behauptet wird, die Masse der Neutrinos wäre imaginär?
Dazu muss man sich eine der wichtigsten Formeln der speziellen Relativitätstheorie von Albert Einstein ansehen:
Sie beschreibt die Energie eines Teilchens. Die muss immer eine reale, beobachtbare Größe mit einem positiven Wert sein. Und das ist normalerweise auch kein Problem. Ist die Geschwindigkeit v eines Teilchens kleiner als die Lichtgeschwindigkeit c, dann wird in der Formel der Ausdruck unter der Wurzel positiv und der Wert der Energie ist eine normale Zahl. Ist die Geschwindigkeit eines Teilchens aber größer als die Lichtgeschwindigkeit, dann ist die Zahl unter der Wurzel negativ. Und wenn man die Wurzel einer negativen Zahl zieht, bekommt man eine imaginäre Zahl. Damit am Ende die Energie trotzdem eine normale Zahl sein kann, muss als Ausgleich die Masse m über dem Bruchstich ebenfalls eine imaginäre Zahl sein. Dann hat man zwei imaginäre Zahlen, die durcheinander geteilt werden und das Ergebnis so einer Rechnung ist immer eine normale Zahl.

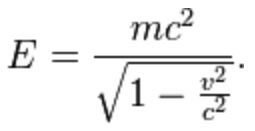










Kommentare (150)