Die ganzen “an” usw sind die Werte für R die ich weiter oben angegeben habe. Ist an zum Beispiel der Wert für die dritte Verdoppelung, dann ist an-1 die für die zweite und an-2 die für die erste. Berechnet man genügend Werte für die Verdoppelungen, dann kann man sie der Reihe nach einsetzen und wird merken, dass sie sich immer weiter der Zahl 4,669… annähern.
So weit, so unspektakulär. Feigenbaum aber fragte sich, warum es genau diese Zahl sein sollte, von der die Abfolge der Periodenverdoppelung bestimmt wird. Keine der üblichen Zahlen aus der Mathematik (Pi, der natürliche Logarithmus e, usw) schienen irgendwie dazu zu passen. Als nächstes wandte Feigenbaum sich anderen mathematischen Modellen zu, die ebenso wie die logistische Gleichung ebenfalls eine Periodenverdoppelung zeigen. Und stellte zu seiner Überraschung fest, dass auch dort die Verdoppelung von genau der gleichen Zahl bestimmt wird!
Heute wird diese Zahl die Feigenbaum-Konstante genannt und mit dem griechischen Buchstaben delta bezeichnet:
Man vermutet, dass die Feigenbaum-Konstante “transzendental” ist, also so wie auch die berühmte Zahl Pi irrational ist und es keine regelmäßige Entwicklung in den Nachkommastellen gibt (und die Zahl auch nicht die Nullstelle eines Polynoms mit ganzzahligen Koeffizienten ist). Bis jetzt hat man knapp über 1000 Nachkommastellen von Feigenbaums Konstante berechnet – seltsam ist sie immer noch geblieben.
Sie demonstriert nicht nur die sogenannte “Universalität” des Chaos, sondern zeigt auch das schwer verständliche Wechselspiel zwischen Unvorhersagbarkeit und mathematischer Exaktheit. Egal welches chaotische System man betrachtet, wenn das Chaos auftritt, dann schwindet die Möglichkeit, Aussagen über dessen Zukunft zu machen, sehr schnell. Chaos eben… Aber gleichzeitig hält sich das Chaos trotzdem an gewisse Regeln. Die Periodenverdoppelung passiert nicht einfach irgendwie, wie man es vielleicht beim Chaos erwarten würde, sondern wird von einer mathematischen Konstanten bestimmt, die in jedem System identisch ist.
Feigenbaums Universalität demonstriert, dass das Chaos in der Natur eben nicht einfach nur schnöde Unordnung ist, sondern das es auch eigentlich simplen Grundregeln entspringt. Die Feigenbaumkonstante beschreibt, wie sich das Chaos bildet und das dabei keine Willkür herrscht. Man kann chaotische Systeme auf verschiedene Art und Weise betrachten und wird immer auf die gleichen Bausteine stoßen. Das Chaos ist nicht nur seltsam, es ist auch “selbstähnlich” und was das heißt, erzähle ich in der nächsten Folge, wenn es um Mandelbrots Fraktale geht!

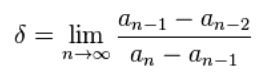










Kommentare (12)