Chaos ist cool! Nein, nicht die Unordnung bei euch zuhause in der Küche. Das ist einfach nur Schlamperei und kein Chaos 😉 Ich spreche vom wissenschaftlichen Chaos und um das wirklich zu durchblicken, sofern das bei so einem Phänomen überhaupt geht, braucht man jede Menge Mathematik. Damit habe ich mich schon früher im Blog (Einleitung, Teil 1, Teil 2, Teil 3, Teil 4) und meinem Podcast (Folge 93) beschäftigt. Da aber vielleicht nicht jeder Lust auf eine lange Auseinandersetzung mit komplizierter Mathematik hat, gibt es seit kurzem meine “Best of Chaos”-Serie, in der ich einfach ein paar meiner chaotischen Lieblingsphänomene vorstelle. Ich habe schon über den “seltsamen Attraktor” gesprochen, dessen Seltsamkeit mich jedes Mal aufs Neue fasziniert. Und beim letzten Mal habe ich von der noch seltsameren Verdoppelung der Perioden erzählt, mit der auch die heutige Folge zu tun hat.
Denn jetzt wird das Chaos universal!

Ein Feigenbaum! Aber um den gehts nicht… (Bild: Gide, CC-BY-SA 3.0)
Eine kurze Zusammenfassung: Das Phänomen der Verdoppelung der Perioden hat man in den 1970er Jahren entdeckt, als man untersuchen wollte, wie sich die Population von Lebewesen im Laufe der Zeit verändert. Man ging davon aus, dass die äußeren Umstände (Nahrungsangebot, Feinde, etc) dafür sorgen, dass sich früher oder später ein Gleichgewichtszustand einstellt und die Größe der Population dann gleich bleibt. Stattdessen hat man festgestellt, dass bei einer Veränderung der Stärke der äußeren Einflüsse etwas anderes passiert: Zuerst gibt es tatsächlich ein normales Gleichgewicht. Ab einer gewissen Stärke wechselt die Größe der Population aber plötzlich zwischen zwei Werten hin und her! Wird der Einfluss noch stärker, dann springt die Größe zwischen vier Werten; danach wechselt sie zwischen 8 Werten hin und her; dann zwischen 16, dann 32, und so weiter. Die Perioden verdoppeln sich immer weiter, bis irgendwann das komplette Chaos ausbricht.
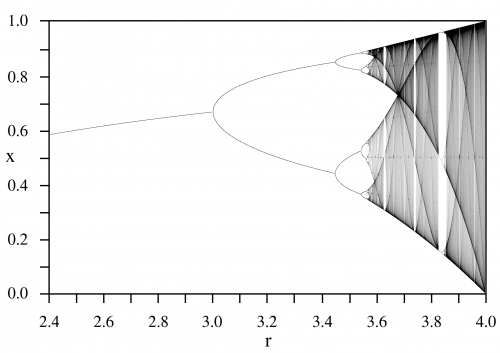
Das allein ist schon seltsam genug und ein Verhalten, dass nicht nur bei der Untersuchung von Populationsgrößen auftritt, sondern immer dann, wenn ein System chaotisch wird. Noch seltsamer (ja ich weiß, dieses Wort verwende ich oft – aber das Chaos IST eben sehr seltsam…) war aber das, was der amerikanische Physiker Mitchell Feigenbaum bei seiner Untersuchung der Periodenverdoppelung entdeckt hat. Ihr erinnert euch noch an das Bild von der logistischen Gleichung vom letzten Mal? So sieht es aus:
Man sieht hier auf der y-Achse die Größe der Population und auf der x-Achse den Wachstumsparameter, also die Zahl, die in dem Modell die Stärke der äußeren Einflüsse angibt. Zuerst zeigt das Diagramm nur eine einfach Linie; die Populationsgröße nimmt also einen Gleichgewichtszustand ein. Dann spaltet sie sich in zwei Äste auf, die dann vier Äste bilden, und so weiter: Das ist die Periodenverdoppelung auf das Chaos folgt, bei der die Linie in eine Wolke aus ungeordneten Punkten übergeht.
Feigenbaum hatte nun nachgesehen, wo genau die Periodenverdoppelungen stattfinden. Ich lade euch wieder ein, euch selbst ein kleines Computerprogramm zu schreiben, dass die logistische Gleichung berechnet bzw. dieses Online-Programm zu nutzen um selbst die Werte des Wachstumsparameters R zu bestimmen, bei denen die Periodenverdoppelungen eintreten. Feigenbaum hat das jedenfalls gemacht: Die erste Verdoppelung fand statt, als R=3 war. Die zweite Verdoppelung passiert, wenn R = 3.4494897… ist. Die dritte Verdoppelung auf vier Äste findet bei R = 3.5440903… statt. 16 Äste gibt es bei R = 3.5644073… und 32 bei R = 3.5687594…
Was ist daran so besonders? Feigenbaum hatte diese Rechnungen angestellt und damals nur einen simplen Taschenrechner zur Verfügung. Es war viel Arbeit, auf diese Weise die jeweils nächsten Verdoppelungspunkte zu berechne. Er verfiel auf die Frage, ob er vielleicht stattdessen irgendwie vorhersagen könnte, wo die nächste Verdoppelung stattfinden würde? Zuerst fiel ihm auf, dass die Zahlen immer näher zusammen rücken, sie konvergieren, wie man in der Mathematik dazu sagt. Sie scheinen auf einen konkreten Grenzwert zuzustreben. Feigenbaum hatte Ahnung von Mathematik und wusste, wie man so einen Grenzwert berechnet. Wer es wissen möchte – mit dieser Formel:
Die ganzen “an” usw sind die Werte für R die ich weiter oben angegeben habe. Ist an zum Beispiel der Wert für die dritte Verdoppelung, dann ist an-1 die für die zweite und an-2 die für die erste. Berechnet man genügend Werte für die Verdoppelungen, dann kann man sie der Reihe nach einsetzen und wird merken, dass sie sich immer weiter der Zahl 4,669… annähern.
So weit, so unspektakulär. Feigenbaum aber fragte sich, warum es genau diese Zahl sein sollte, von der die Abfolge der Periodenverdoppelung bestimmt wird. Keine der üblichen Zahlen aus der Mathematik (Pi, der natürliche Logarithmus e, usw) schienen irgendwie dazu zu passen. Als nächstes wandte Feigenbaum sich anderen mathematischen Modellen zu, die ebenso wie die logistische Gleichung ebenfalls eine Periodenverdoppelung zeigen. Und stellte zu seiner Überraschung fest, dass auch dort die Verdoppelung von genau der gleichen Zahl bestimmt wird!
Heute wird diese Zahl die Feigenbaum-Konstante genannt und mit dem griechischen Buchstaben delta bezeichnet:
Man vermutet, dass die Feigenbaum-Konstante “transzendental” ist, also so wie auch die berühmte Zahl Pi irrational ist und es keine regelmäßige Entwicklung in den Nachkommastellen gibt (und die Zahl auch nicht die Nullstelle eines Polynoms mit ganzzahligen Koeffizienten ist). Bis jetzt hat man knapp über 1000 Nachkommastellen von Feigenbaums Konstante berechnet – seltsam ist sie immer noch geblieben.
Sie demonstriert nicht nur die sogenannte “Universalität” des Chaos, sondern zeigt auch das schwer verständliche Wechselspiel zwischen Unvorhersagbarkeit und mathematischer Exaktheit. Egal welches chaotische System man betrachtet, wenn das Chaos auftritt, dann schwindet die Möglichkeit, Aussagen über dessen Zukunft zu machen, sehr schnell. Chaos eben… Aber gleichzeitig hält sich das Chaos trotzdem an gewisse Regeln. Die Periodenverdoppelung passiert nicht einfach irgendwie, wie man es vielleicht beim Chaos erwarten würde, sondern wird von einer mathematischen Konstanten bestimmt, die in jedem System identisch ist.
Feigenbaums Universalität demonstriert, dass das Chaos in der Natur eben nicht einfach nur schnöde Unordnung ist, sondern das es auch eigentlich simplen Grundregeln entspringt. Die Feigenbaumkonstante beschreibt, wie sich das Chaos bildet und das dabei keine Willkür herrscht. Man kann chaotische Systeme auf verschiedene Art und Weise betrachten und wird immer auf die gleichen Bausteine stoßen. Das Chaos ist nicht nur seltsam, es ist auch “selbstähnlich” und was das heißt, erzähle ich in der nächsten Folge, wenn es um Mandelbrots Fraktale geht!

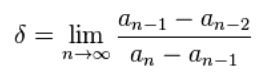










Kommentare (12)