Weiters wird festgestellt, dass die gefundenen Planeten sich alle in der Nähe des Stabilitätslimits befinden. Man kann durch numerische Simulationen herausfinden, wie nahe ein Planet den beiden Sternen kommen kann, bevor eine stabile Bewegung nicht mehr möglich und die gravitativen Störungen zu groß sind. Diese Grenze hängt von der Masse und der Umlaufbahn der Sterne selbst ab. Und es ist durchaus interessant, dass die Planeten alle in der Nähe dieser Grenze sind. Theoretisch könnten sie ja irgendwo außerhalb dieser Grenze sein.
Außerdem bewegen sich die Planeten alle mehr oder weniger in der selben Ebene wie die Sterne selbst. Das aber ist auf einen Auswahleffekt bei den Beobachtungen zurückzuführen. Da die Planeten mit der Transitmethode entdeckt worden sind, können sie nur annähernd in der gleichen Ebene wie die Sterne liegen. Ansonsten hätte man die Verdunkelung des Sternenlichts nicht bemerkt, wenn die Planeten von der Erde aus gesehen vor den Sternen vorüber ziehen. Schließlich stellen Martin und seine Kollegen noch fest, dass die entdeckten Planeten alle eine Masse haben, die zwischen der 3 und 8,3fachen Erdmasse liegt und dass im Durchschnitt 10 Prozent aller Doppelsterne CBPs haben.
Nach dieser genaueren Datenanalyse wird es dann in Abschnitt 3 richtig interessant, denn jetzt kommt die Theorie:
“To a first approximation, a hierarchical triple star system can be modelled as an inner binary of two stars and an outer binary composed of the inner binary, located at its centre of mass, and the outer tertiary star. Both binaries move on Keplerian orbits which we define using osculating orbital elements for the period, P, semi-major axis, a, eccentricity, e, argument of periapse, ω, and longitude of the ascending node, Ω, where we denote the inner and outer binaries with subscripts “in” and “out”, respectively. The two orbits are inclined with respect to each other by ΔIin,out. The inner binary stars have masses M1 and M2 and the tertiary mass is M3.”
Es ist ein wenig seltsam, dass dieser Teil so ausführlich beschrieben wird. Für jeden Himmelsmechaniker sollte es klar sein, dass man die Bahnelemente (die ich hier genau beschrieben habe) benutzen muss, wenn man die Bewegung von mehreren Himmelskörpern beschreiben will. Wer nicht weiß, worum es sich dabei handelt, wird so einen Artikel auch nicht im Detail lesen. Allerdings weiß ich aus eigener Erfahrung, dass man NIE genug Informationen haben kann, was die Notation angeht, wenn man fremde Artikel liest. Wenn man die Arbeit selbst nachvollziehen will, muss man ganz genau wissen, was die einzelnen Variablen der fremden Autoren bedeuten.
So richtig heftig wird es dann aber erst im nächsten Absatz:
“In the quadrupole approximation of the Hamiltonian of the system the tertiary star remains on a static orbit whilst its perturbations induce a nodal and apsidal precession on the inner binary”
Hier stoße ich dann auch an die Grenzen dessen, was hier im Rahmen dieses Blogs möglich ist. Wollte ich ausführlich und vor allem allgemeinverständlich erklären, was man sich unter einer “quadrupole approximation of the Hamiltonian” vorstellen soll, müsste ich wohl erst ein halbes Buch verfassen. Im Prinzip geht es aber um folgendes.
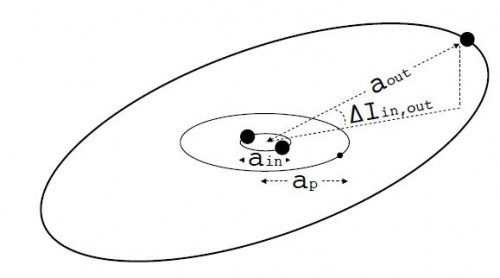
Das Modell (Bild: Martin et al, 2015)
Das Modell mit dem die Astronomen arbeiten, besteht aus drei Sternen. Zwei davon umkreisen sich gegenseitig auf ganz normalen Bahnen, die durch die Kepler-Gesetze vorgegeben werden und die durch die oben erwähnten Bahnelemente beschrieben werden. Außerdem existiert ein dritter Stern, der weit entfernt von den beiden anderen um diese herum kreist. Dessen Bewegung wird in einem Modell betrachtet, bei dem die beiden inneren Sterne zu einem fiktiven Stern zusammengefasst werden. Es gibt also zwei “Doppelsternsystem”; eines besteht aus den beiden inneren Sternen und eines aus dem dritten äußeren und dem fiktiven “Doppelinnenstern”. Würde man die Bewegung der drei Sterne vollständig beschreiben wollen, wäre das unmöglich, denn es existiert keine exakte mathematische Lösung für die Bewegung von mehr als zwei Himmelskörpern unter ihrer gemeinsamen Gravitationskraft. Man kann aber eine Näherungslösung bekommen, wenn man die Angelegenheit entkoppelt und als zwei Systeme aus jeweils zwei Körpern betrachtet, so wie Martin und seine Kollegen es tun. Die Sache mit der “quadrupole approximation of the Hamiltonian” bezieht sich auf die mathematischen Methoden der Störungsrechnung (wer mehr darüber wissen will, kann meine Serie dazu lesen: Teil 1, Teil 2, Teil 3, Teil 4) mit denen hier gearbeitet wird. Es läuft daraus hinaus, dass die Bahn des dritten Sterns selbst konstant bleibt, seine gravitativen Störungen auf die Bewegung der beiden inneren Sterne aber im Modell berücksichtigt werden.











Kommentare (92)