Ich schreibe hier in meinem Blog oft über aktuelle astronomische Forschung. Meistens erkläre ich dann kurz die Grundlagen, auf denen die jeweilige Forschungsarbeit basiert, probiere die Ergebnisse der Wissenschaftler verständlich zusammenzufassen und gehe dann vielleicht noch auf ein oder zwei interessante Details ein. Aber ich dachte mir, dass es auch mal ganz interessant sein kann, eine komplette wissenschaftliche Facharbeit von Anfang bis Ende durchzugehen und dabei zu “übersetzen”. So bekommt man vielleicht einen besseren Einblick in die tatsächliche Arbeit der Wissenschaftler – denn die ganzen technischen Details werden in den üblichen Pressemitteilungen meistens übergangen obwohl sie unter Umständen durchaus interessant sein können. Ich probiere das jetzt einfach mal – und freue mich über Feedback. Je nachdem wie das ausfällt, werde ich das in Zukunft weiterführen oder auch nicht.
——————————————————-
David Martin, Tsevi Mazeh und Daniel Fabrycky sind drei Namen, die regelmäßigen Lesern der himmelsmechanischen Fachliteratur bekannt sein dürften. Aber wer diese drei Astronomen nicht kennt, muss sich keine Sorgen machen. Die Zielgruppe für wissenschaftliche Arbeiten aus diesem Themenbereich ist nicht besonders groß. Interessant sind die Ergebnisse aber trotzdem und darum möchte ich mich heute mit dem Artikel “No circumbinary planets transiting the tightest Kepler binaries – a fingerprint of a third star” beschäftigen. Es geht um extrasolare Planeten, die sich in Dreifachsternsystemen befinden und die Einleitung klingt auf jeden Fall schon sehr vielversprechend:
“The first two decades of exoplanetary science have yielded many surprising results. Not only do most stars host orbiting planets (Cassan et al. 2012), but planets are often found in unexpected locations and with unexpected properties. For example, hot-Jupiters continue to pose significant theoretical challenges (Triaud et al. 2010; Madhusudhan et al. 2014), while Super-Earths were predicted not to form, and yet they are some of the most abundant planets known today (Howard et al. 2010). Planets also have been found in binary star systems orbiting one (e.g., 16 Cygni, Cochran et al. 1997) and two (e.g., Kepler-16, Doyle et al. 2011) stars. The parameter space of non-discoveries is shrinking fast. The field has therefore evolved to a state where an absence of planets is just as telling as a new discovery.”
Normalerweise ist der “Introduction”-Abschnitt eines wissenschaftlichen Artikels ja vor allem dazu da, Dinge zu erzählen, die eigentlich sowieso schon jeder weiß, der sich für das Thema interessiert. Und natürlich dafür, so viele Kollegen wie nur möglich zu zitieren, damit sich auch niemand übergangen fühlt. Denn man weiß ja nie, wer von diesen Leuten von der Zeitschrift in der man veröffentlichen will, als Gutachter ausgewählt wird! In diesem Fall hat mich aber der letzte Satz ein bisschen überrascht. Zuerst erklären die Autoren, dass man bei der Suche nach extrasolaren Planeten mittlerweile große Fortschritte gemacht hat. Man hat fast überall Planeten gefunden und unter anderem auch Planeten, die sich in Doppelsternsystemen befinden. Vor allem hat man aber nun schon so viele Planeten an so vielen verschiedenen Orten entdeckt, dass es auch relevant ist, wenn man irgendwo keine Planeten findet! “An absence of planets is just as telling as a new discovery”, sagen Martin und seine Kollegen. Da man wirklich überall Planeten gefunden hat, muss es etwas zu bedeuten haben, wenn man irgendwo keine Planeten finden kann. Und einen solchen Fall abwesender Planeten wollen Martin, Mazeh und Fabrycky in ihrer Arbeit behandeln:
“One conspicuous absence is seen in the Kepler circumbinary planets (CBPs). So far there have been ten transiting CBPs discovered by Kepler orbiting eight eclipsing binaries (EBs), including the three-planet system Kepler-47 (Orosz et al. 2012b). It was pointed out byWelsh et al. (2014a) that all of the planets have been found orbiting EBs of periods between 7.4 and 40 d, despite the median of the EB catalog being 2.7 d. The discoveries have therefore been made on the tail of the EB period distribution and there is a dearth of planets around the shortest-period binaries.”
Die Wissenschaftler haben sich also alle Planeten angesehen, die vom Weltraumteleskop Kepler in Doppelsternsystemen entdeckt worden sind. Und zwar diejenigen Planeten, die außen um beide Sterne herum kreisen: Die sogenannten “Circumbinary Planets (CBPs)”. Manche Leute sind ja immer noch überrascht, dass es Planeten in Doppelsternsystemen überhaupt geben kann. Aber es ist eigentlich schon lange klar, dass das durchaus möglich ist. Ich habe das hier ein wenig ausführlicher erklärt. Es gibt zwei Bereiche, in denen sich ein Planet in einem Doppelsternsystem stabil bewegen kann: Er kann einen der beiden Sterne umkreisen und wenn der andere Stern ausreichend weit entfernt ist, dann ist dessen Anziehungskraft zu gering, um einen störenden Einfluss auf den Planeten auszuüben. Oder aber der Planet kreist außen um beide Sterne herum und ist weit genug von ihnen entfernt, so dass er den kombinierten Einfluss beider Sterne spürt. Aus der Sicht des Planeten fühlt es sich dann so an, als wäre in der Mitte seiner Umlaufbahn nur ein Stern, dessen Masse so groß ist wie die addierte Masse der beiden einzelnen Sterne. Die beiden Fälle werden “S-Typ” und “P-Typ” genannt:
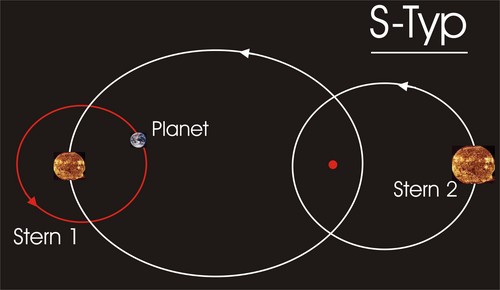
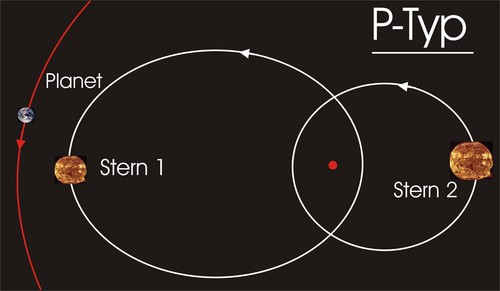
Ihre Hypothese geht auf die Entstehung der Doppelsternsysteme zurück:
“It is generally believed that most very close binaries (< 7d) are initially formed at wider separations. The binaries subsequently shrink under the influence of a misaligned tertiary star and a process known as Kozai cycles with tidal friction (KCTF).”
Man geht derzeit davon aus, dass die sehr engen Doppelsternsysteme nicht schon so eng entstanden sind. Früher waren die Sterne weiter auseinander und haben sich erst später angenähert. Der Grund dafür ist die Existenz eines dritten Sterns und ein Mechanismus der “Kozai-Zyklus mit Gezeitenreibung” (Kozai cycles with tidal friction – KCTF) heißt. Die Astronomen wollen nun demonstrieren, dass genau dieser Mechanismus auch dazu führt, dass in solchen Systemen auch keine Planeten existieren können (sie merken außerdem an, dass sie nicht die ersten sind, die diese Idee hatten).
Jetzt kommen im Artikel die Abschnitte, die man normalerweise nur dann liest, wenn man selbst vor hat, auf genau diesem Gebiet wissenschaftlich zu arbeiten. Wenn man einfach nur daran interessiert ist herauszufinden, was die Leute gemacht haben, beschränkt man sich meistens auf die Lektüre der Einleitung und der Zusammenfassung am Schluss. Den technischen Kram dazwischen überlasst man dann den eigentlichen Experten. Aber heute springen wir nicht gleich zum Ende sondern lesen weiter! (Ich werde jetzt aber trotzdem nicht alles zitieren und im Einzelnen erläutern)
Nachdem die Autoren zuerst einmal genau erklärt haben, woher sie die ihrer Arbeit zugrunde liegenden Daten bezogen haben und die Daten der 10 Planeten in den 8 Doppelsternsystemen in einer Tabelle aufgelistet haben, machen sie sich an eine erste Analyse:
“In the small sample of CBPs some preliminary trends have been identified:”
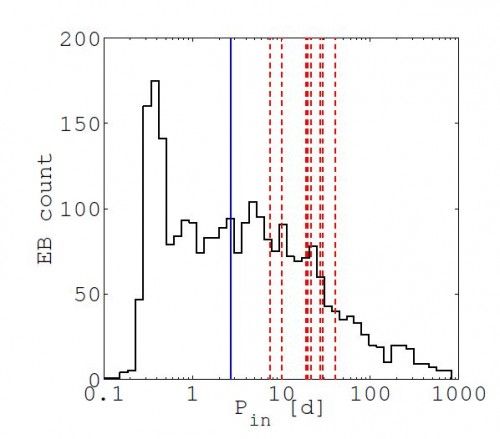
Man kann zwar darüber streiten, ob es wirklich sinnvoll ist, aus nur 10 Datensätzen schon Trends ableiten zu wollen. Aber wenn man weiß, was man machen kann und was nicht, ist eigentlich nichts dagegen einzuwenden. Die Autoren stellen zuerst noch einmal fest, dass sich Planeten eher bei Doppelsternen mit langen Umlaufzeiten finden und stellen den Befund noch einmal mit einer Grafik dar:
Die schwarzen Linien geben an, wie viele Eclipsing Binaries mit entsprechenden Umlaufzeiten (aufgetragen auf der x-Achse) entdeckt worden sind. Die roten Linien zeigen, wo man Planeten entdeckt hat und die blaue Linie definiert den Median. Es ist klar zu sehen, dass die Planeten sich alle auf der rechten Seite des Diagramms befinden, wo die langen Umlaufzeiten sind.
Weiters wird festgestellt, dass die gefundenen Planeten sich alle in der Nähe des Stabilitätslimits befinden. Man kann durch numerische Simulationen herausfinden, wie nahe ein Planet den beiden Sternen kommen kann, bevor eine stabile Bewegung nicht mehr möglich und die gravitativen Störungen zu groß sind. Diese Grenze hängt von der Masse und der Umlaufbahn der Sterne selbst ab. Und es ist durchaus interessant, dass die Planeten alle in der Nähe dieser Grenze sind. Theoretisch könnten sie ja irgendwo außerhalb dieser Grenze sein.
Außerdem bewegen sich die Planeten alle mehr oder weniger in der selben Ebene wie die Sterne selbst. Das aber ist auf einen Auswahleffekt bei den Beobachtungen zurückzuführen. Da die Planeten mit der Transitmethode entdeckt worden sind, können sie nur annähernd in der gleichen Ebene wie die Sterne liegen. Ansonsten hätte man die Verdunkelung des Sternenlichts nicht bemerkt, wenn die Planeten von der Erde aus gesehen vor den Sternen vorüber ziehen. Schließlich stellen Martin und seine Kollegen noch fest, dass die entdeckten Planeten alle eine Masse haben, die zwischen der 3 und 8,3fachen Erdmasse liegt und dass im Durchschnitt 10 Prozent aller Doppelsterne CBPs haben.
Nach dieser genaueren Datenanalyse wird es dann in Abschnitt 3 richtig interessant, denn jetzt kommt die Theorie:
“To a first approximation, a hierarchical triple star system can be modelled as an inner binary of two stars and an outer binary composed of the inner binary, located at its centre of mass, and the outer tertiary star. Both binaries move on Keplerian orbits which we define using osculating orbital elements for the period, P, semi-major axis, a, eccentricity, e, argument of periapse, ω, and longitude of the ascending node, Ω, where we denote the inner and outer binaries with subscripts “in” and “out”, respectively. The two orbits are inclined with respect to each other by ΔIin,out. The inner binary stars have masses M1 and M2 and the tertiary mass is M3.”
Es ist ein wenig seltsam, dass dieser Teil so ausführlich beschrieben wird. Für jeden Himmelsmechaniker sollte es klar sein, dass man die Bahnelemente (die ich hier genau beschrieben habe) benutzen muss, wenn man die Bewegung von mehreren Himmelskörpern beschreiben will. Wer nicht weiß, worum es sich dabei handelt, wird so einen Artikel auch nicht im Detail lesen. Allerdings weiß ich aus eigener Erfahrung, dass man NIE genug Informationen haben kann, was die Notation angeht, wenn man fremde Artikel liest. Wenn man die Arbeit selbst nachvollziehen will, muss man ganz genau wissen, was die einzelnen Variablen der fremden Autoren bedeuten.
So richtig heftig wird es dann aber erst im nächsten Absatz:
“In the quadrupole approximation of the Hamiltonian of the system the tertiary star remains on a static orbit whilst its perturbations induce a nodal and apsidal precession on the inner binary”
Hier stoße ich dann auch an die Grenzen dessen, was hier im Rahmen dieses Blogs möglich ist. Wollte ich ausführlich und vor allem allgemeinverständlich erklären, was man sich unter einer “quadrupole approximation of the Hamiltonian” vorstellen soll, müsste ich wohl erst ein halbes Buch verfassen. Im Prinzip geht es aber um folgendes.
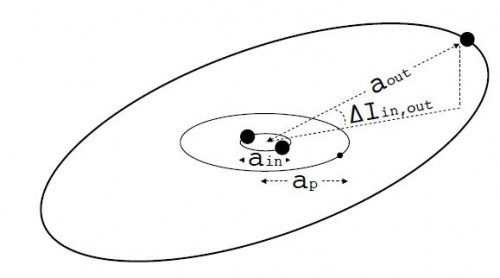
Das Modell (Bild: Martin et al, 2015)
Das Modell mit dem die Astronomen arbeiten, besteht aus drei Sternen. Zwei davon umkreisen sich gegenseitig auf ganz normalen Bahnen, die durch die Kepler-Gesetze vorgegeben werden und die durch die oben erwähnten Bahnelemente beschrieben werden. Außerdem existiert ein dritter Stern, der weit entfernt von den beiden anderen um diese herum kreist. Dessen Bewegung wird in einem Modell betrachtet, bei dem die beiden inneren Sterne zu einem fiktiven Stern zusammengefasst werden. Es gibt also zwei “Doppelsternsystem”; eines besteht aus den beiden inneren Sternen und eines aus dem dritten äußeren und dem fiktiven “Doppelinnenstern”. Würde man die Bewegung der drei Sterne vollständig beschreiben wollen, wäre das unmöglich, denn es existiert keine exakte mathematische Lösung für die Bewegung von mehr als zwei Himmelskörpern unter ihrer gemeinsamen Gravitationskraft. Man kann aber eine Näherungslösung bekommen, wenn man die Angelegenheit entkoppelt und als zwei Systeme aus jeweils zwei Körpern betrachtet, so wie Martin und seine Kollegen es tun. Die Sache mit der “quadrupole approximation of the Hamiltonian” bezieht sich auf die mathematischen Methoden der Störungsrechnung (wer mehr darüber wissen will, kann meine Serie dazu lesen: Teil 1, Teil 2, Teil 3, Teil 4) mit denen hier gearbeitet wird. Es läuft daraus hinaus, dass die Bahn des dritten Sterns selbst konstant bleibt, seine gravitativen Störungen auf die Bewegung der beiden inneren Sterne aber im Modell berücksichtigt werden.
Diese Störungen verursachen vor allem eine Veränderung der Exzentrizität in der Umlaufbahn der beiden inneren Sterne. Denn die beiden müssen einander ja nicht auf einer Kreisbahn umlaufen. Es kann genau so gut eine elliptische Bahn sein und wie stark die Umlaufbahn von einem Kreis abweicht, gibt die Exzentrizität an. Außerdem ändert sich durch die Störung der Winkel zwischen der Ebene in denen die beiden inneren Sterne einander umlaufen und der Ebene, in der sich der dritte Stern außen um beide herum bewegt.
Diese Störungen – die Variationen in der Exzentrizität und des Neigungswinkels der Bahnen – sind die weiter oben angesprochenen “Kozai Cycles” und die Zeitskala, auf der die Veränderungen stattfinden, werden durch diese Formel beschrieben:
Ich habe diese Formel hier nicht eingefügt, um sie im Detail zu erklären. Das würde viel zu weit führen. Aber man kann an ihr zumindest ein bisschen von der Methodik der Störungsrechnung erkennen. Eine exakte Lösung der Bewegung von mehreren Himmelskörpern ist ja wie gesagt nicht möglich. Aber in der Störungsrechnung arbeitet man mit Annäherungen: Man geht von einem lösbaren Fall aus (dem Zweikörperproblem) und fügt dann dieser exakten Lösung der Reihe nach kleinere Störungen hinzu, solange bis die gewünschte Genauigkeit erreicht ist. Dabei verwendet man mathematische Reihe, also im Allgemeinen unendlich lange Summen, bei denen jeder Term ein bisschen kleiner ist als der vorhergehende. Man kann diese unendliche Addition also irgendwo mitten drin abbrechen und trotzdem sicher sein, dass der Rest, den man ignoriert hat, nicht beliebig groß wird und der Fehler den man mit der Methode macht daher entsprechend klein bleibt. Ein typisches Zeichen für die Verwendung dieser mathematischen Reihen sind die Brüche (2/3) und Ausdrücke der Form (1-e²)3/2.
Nachdem die Autoren jetzt noch (ganz wichtig!) angegeben haben, mit welchem Softwarepaket sie all die numerischen Rechnungen durchgeführt haben, gehen sie im nächsten Abschnitt nochmal genauer auf die “Kozai Cycles” ein:
“Kozai cycles are the result of small perturbations induced by the tertiary star which build up coherently over the apsidal precession period. If there is an additional secular perturbation causing an apsidal precession of the binary on a shorter timescale, then the coherent eccentricity modulation is partially lost. Consequently, the amplitude of the tertiary’s perturbations decreases and the Kozai effect is suppressed. If the inner binary stars are close enough then apsidal precession due to general relativity and tidal and rotational bulges can suppress the Kozai modulation (Wu & Murray 2003; Fabrycky & Tremaine 2007). Alternatively, a suffciently close and massive circumbinary planet may also suppress the Kozai modulation”
Aber zuerst sollte ich nochmal kurz etwas allgemein zum Kozai-Zyklus beziehungsweise der Kozai-Resonanz sagen. Über himmelsmechanische Resonanzen habe ich ja früher schon einen ausführlichen Artikel geschrieben. Sie treten immer dann auf, wenn die Periode der Bewegung von zwei Himmelskörper in einem ganzzahligen Verhältnis zueinander steht. Wenn sich zum Beispiel ein Asteroid in der gleichen Zeit zweimal um die Sonne bewegt, in der der Jupiter eine Runde schafft, dann stehen sie in einer “2:1 Resonanz” der mittleren Bewegung. Dann können sich die gravitativen Störungen die Jupiter auf den Asteroid ausübt, im Laufe der Zeit aufschaukeln und dessen Bahn massiv verändern. Es gibt aber auch noch die sogenannten “säkularen Resonanzen”. Hier geht es nicht um die konkrete Bewegung der Himmelskörper selbst, sondern um die Veränderungen ihrer Bahn. So eine Umlaufbahn bleibt ja nicht konstant sondern ändert sich. Sie wird größer und kleiner, kreisförmiger und weniger kreisförmig und wackelt im Raum hin und her (das sind die sogenannten “Milankovic-Zyklen” über die ich hier gesprochen habe). Wenn jetzt zum Beispiel die Periode, mit der die Bahn eines Asteroiden im Raum hin und her wackelt in einem ganzzahligen Verhältnis zur Wackelperiode der Bahn des Jupiters steht, dann befinden sie sich in einer säkularen Resonanz, was ebenso zu großen Störungen führen kann.
Ein Spezialfall bei den Resonanzen ist jetzt aber die Kozai-Resonanz. Auch hier würde es viel zu weit führen, wenn ich diesen Effekt im Detail ableiten wollen würde. Es geht darum, dass die gravitativen Störungen zwischen den Himmelskörpern zwar (unter anderem) die Exzentrizität und die Neigung der Bahn verändern können, aber unter bestimmten Voraussetzungen eine Kombination dieser beiden Werte immer konstant bleiben muss (sie ist dann in diesem System eine Erhaltungsgröße wie die Energie oder der Drehimpuls). Das heißt nichts anderes als dass dann zum Beispiel die Exzentrizität der Bahn kleiner werden muss, wenn die Neigung der Bahn größer wird und umgekehrt. Dieses Auf-und-Ab sind die “Kozai Cycles” von denen im Artikel die Rede ist. Wie Martin und seine Kollegen aber anmerken, kann der Kozai-Effekt in ihrem Modell auch abgeschwächt werden, wenn verschiedene andere Resonanzen auf die richtige Art und Weise zusammenwirken. Beziehungsweise man die relativistischen Effekte der Bewegung oder Gezeitenkräfte im Modell berücksichtigt. Sogar die Störungen die ein Planet durch seine Gravitationskraft auf die Sterne ausübt, kann zu einer Abschwächung des Kozai-Effekts führen.
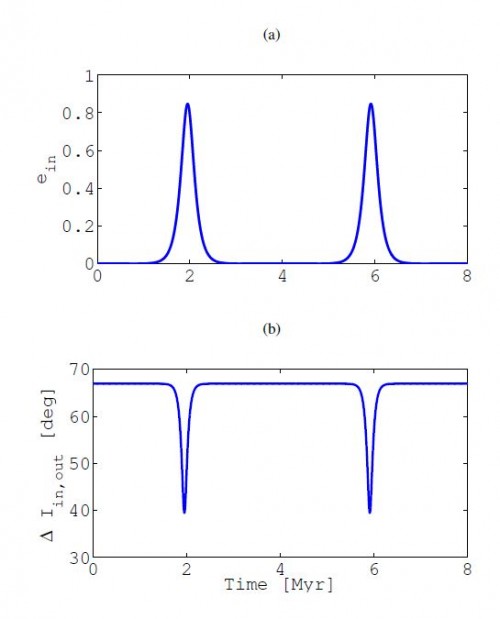
Beispiel für den Kozai-Effekt. Das obere Bild zeigt, wie sich die Exzentrizität der Umlaufbahn der beiden innern Sterne im Laufe von 8 Millionen Jahren ändert; das untere Bild zeigt die Veränderung der Bahnneigung in Bezug auf die Bahn des dritten Sterns. Die Änderungen laufen genau gegengleich ab (Bild: Martin et al, 2015)
Bevor Martin und seine Kollegen jetzt aber erklären, wozu sie den Kozai-Effekt in ihrer Arbeit überhaupt brauchen, gehen sie Abschnitt 4 des Artikels noch einmal im Detail auf die Bewegung von Planeten in Doppelsternsystemen ein. Sie beginnen wieder mit einer Definition:
“There are two possible planetary orbits in binary star systems:
(i) a circumbinary orbit around both stars or
(ii) a circumprimary orbit around one of the two stars”
Die finde ich persönlich ein wenig doof, weil das “circumprimary” missverständlich ist, wie die Autoren selbst in einer Fussnote anmerken: “Technically a circumprimary orbit only refers to when a planet orbits the bigger of the two stars and an orbit around the smaller star is a circumsecondary orbit, but for simplicity in this paper we will use the term circumprimary to refer to either case.”
Warum sie trotzdem auf diese Notation beharren und Planeten, die beide Sterne umlaufen “circumbinaries” nennen und Planeten die nur einen Stern umkreisen als “circumprimary” bezeichnen, kann ich nicht ganz nachvollziehen – vor allem weil ja auch die klarere “P-Typ” und “S-Typ” (was übrigens für “Planeten-Typ” und “Satelliten-Typ” steht) existiert. Aber ich bin da auch nicht objektiv, weil diese Definition von meiner ehemaligen Arbeitsgruppe in Wien eingeführt wurde. Und der Chef dieser Arbeitsgruppe wird auch im nächsten Absatz zitiert:
“There are restrictions on where a planet may orbit stably in a binary star system, primarily as a function of the binary’s semi-major axis (e.g., Dvorak 1986; Holman & Wiegert 1999). Planets orbiting on the wrong side of the stability limit are generally ejected from the system by a process of resonance overlap”
Hier beziehen sich Martin und seine Kollegen auf die frühen theoretischen Arbeiten, bei denen berechnet wurde, wo sich bei Doppelsternen stabile Bahnen für Planeten befinden. Die erste dieser Arbeiten stammt von Rudolf Dvorak, mein ehemaliger Chef und Doktorvater. Ich finde es heute immer noch bemerkenswert, dass er schon 1986 untersucht hat, wo es bei Doppelsterne stabile Bahnen für Planeten gibt, obwohl damals noch kein einziger extrasolarer Planet entdeckt worden war. In Arbeiten die sich mit Planeten bei Doppelsternen beschäftigen wird aber meistens auf die spätere Arbeit von Holman & Wiegert aus dem Jahr 1999 verwiesen, die mit den dann schon viel besseren Computern auch genauere Rechnungen durchführen konnten und die Stabilitätsgrenzen genauer bestimmen konnten. Wie diese Grenze berechnet wird, zeigt die nächste Formel im Artikel, die ich jetzt aber nicht im Detail erklären werde. Es reicht zu wissen, dass der Abstand der Grenze vom Doppelstern von drei Größen abhängt: Dem Verhältnis der Sternmassen, dem Abstand der Sterne und der Exzentrizität ihrer Umlaufbahn.
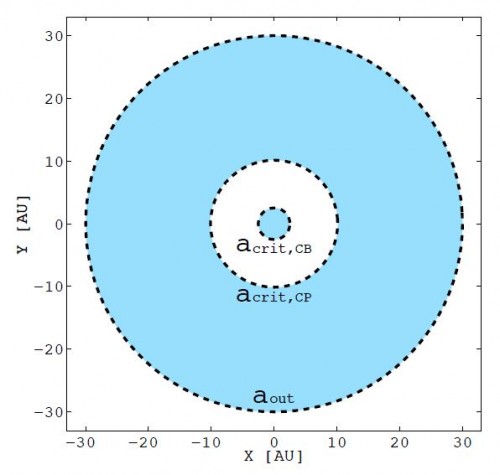
Im nächsten Abschnitt geht es um die “säkulare Entwicklung” der Umlaufbahnen der Sterne umeinander. Genauer gesagt um die “nodal and apsidal precession”. Damit ist die Drehung der Bahn um zwei der drei Richtungen im Raum gemeint (der dritte mögliche Drehwinkel wäre die Bahneigung). In der Arbeit von Martin und seinen Kollegen geht es aber ja um Planeten, die sich in Dreifachsternsystemen befinden und das ist der Thema von Abschnitt 4.2. Hier wird es knifflig. Erinnern wir uns das Modell mit den beiden entkoppelten Doppelsternen (der eine reale, mit den inneren Sternen und der zweite mit dem dritten und dem “fiktiven” Stern). Der Planet ist in Bezug auf die beiden inneren Sterne ein “circumbinary” (p-Typ). In Bezug auf das Doppelsternsystem mit dem äußeren dritten Stern ist er aber ein “circumprimary” (s-Typ) weil er ja den fiktiven Stern (bestehend aus den beiden inneren Sternen) umkreist. Will man etwas über die Stabilität der Bewegung des Planeten wissen, dann muss man die Stabilitätsgrenzen für beide Fälle berücksichtigen. Damit man sich das besser vorstellen kann, bringen die Autoren ein Beispiel für ein Dreifachsternsystem, bei die inneren beiden Sterne 0,5 Astronomische Einheiten (1 AE = 150 Millionen Kilometer) voneinander entfernt sind und der äußere dritte Stern 30 AE von den beiden inneren entfernt ist:
Alles was in diesem Bild blau ist, ist instabil. Ein Planet könnte dort nicht existieren, sondern würde mit einem der Sterne kollidieren oder aus dem System rausfliegen. Nur wenn weit genug vom dritten Stern entfernt und gleichzeitig den beiden inneren Sternen nicht zu nahe ist, also im weißen Bereich in der Mitte des Bildes, kann er sich auf einer stabilen Bahn bewegen. Aber auch wenn er sich in der stabilen Region befindet, heißt das nicht, dass der Planet keinen Störungen ausgesetzt ist – es sind eben nur Störungen, die normalerweise nicht allzu groß werden und sich nur innerhalb gewisser Grenzen auswirken können. Die Astronomen schreiben:
“A planet orbiting within the stability region of a misaligned triple star system is perturbed by two competing secular effects: precession due to the inner binary and Kozai cycles due to the outer binary”
Von den beiden inneren Sternen wird die Bahn des Planeten also auf eine Weise gestört, die zu einer kontinuierlichen Drehung der Bahn führt (“precession”); der dritte äußere Stern erzeugt die oben beschriebene Kozai-Resonanz und lässt Bahnneigung und Exzentrizität der Planetenbahn variieren. Wie sich diese beiden Störungen konkret auswirken, hängt vom Spezialfall ab. Weiter oben habe ich ja erwähnt, dass der Kozai-Effekt auch unterdrückt werden kann. Und das ist näherungsweise dann der Fall, wenn die Störungen durch die inneren Sterne mit einer langsameren Periode stattfinden als die Kozai-Zyklen die vom dritten Stern ausgelöst werden. Um ein vollständiges Bild der Dynamik zu erhalten, muss man jetzt noch untersuchen, wie sich die gravitativen Störungen des Planeten auf die Bewegung der Sterne auswirken. Denn die bestimmt ja wiederum die Störung, die auf den Planeten wirkt (Hey, niemand hat behauptet, Himmelsmechanik wäre nicht knifflig!). Und um das zu berechnen, muss man jetzt wirklich ganz tief in die mathematische Trickkiste der Störungsrechnung greifen! Das kann ich hier schlicht und einfach nicht erklären (denn dann müsste ich wirklich ein Buch schreiben und dieses Buch steht ja auf der Liste der Dinge die ich gerne machen würde aber nicht machen werde). Ich zeige euch nur, wie so etwas aussieht:
Die Funktion “F” ganz oben in dieser Liste ist die Hamilton-Funktion die im Prinzip die Energie beschreibt, die im ganzen System steckt. Kennt man die Hamilton-Funktion kann man damit die Gleichungen aufstellen, die beschreiben, wie sich alles bewegt. Um diese Funktion aufstellen zu können, muss man sich aber meistens mit Annäherungen begnügen, die durch Störungsrechnung gefunden werden können und wie die in diesem Fall aussehen, zeigen die restlichen Funktionen in der Liste. Diese Rechnungen anzustellen ist alles andere als trivial und wirklich nur etwas für ganz begeisterte Himmelsmechaniker. Martin und seine Kollegen haben auch verzichtet, die ganze dahinter stehende Mathematik im Detail aufzulisten und einfach auf die entsprechende Literatur verwiesen (was dann bei den Kollegen für große Begeisterung sorgt, die das ganze nachrechnen müssen, wenn sie die Arbeit tatsächlich komplett nachvollziehen wollen).
Die Arbeit müsste man sich eigentlich nicht antun. Heutzutage hat man ja schnelle Computer und könnte das ganze Problem ganz einfach numerisch am Computer simulieren. Das geht – je nach Methode – mit fast beliebiger Genauigkeit und man würde sich die ganzen mühsamen Rechnungen sparen und könnte gleichzeitig auf die mathematischen Näherungen verzichten sondern wirklich alle dynamischen Effekte inkludieren. Der Nachteil an diesem Simulationsansatz ist aber, dass man dann keine Ahnung, wie sich die dynamischen Effekte im Detail auswirken und welche Rolle welcher Effekt spielt. In so eine Simulation steckt man den Ort der Himmelskörper hinein und bekommt den Ort der Himmelskörper heraus, den sie zu einem späteren Zeitpunkt einnehmen. Das ist in vielen Fällen enorm nützlich. Aber eben nicht immer. Denn wenn man es geschafft hat, sich eine Hamilton-Funktion zu basteln, dann kann man die auch analysieren. So zum Beispiel:
Hier haben Martin und seine Kollegen aus der Hamilton-Funktion eine Formel (20) abgeleitet, die angibt, wie sich die Exzentrizität der Umlaufbahn der beiden inneren Sterne in Abhängigkeit der Neigung zwischen der Bahnebene des äußeren dritten Sterns und der Bahnebene der inneren Sterne verändert. So etwas ist enorm wertvoll, wenn man verstehen will, was in solchen Systemen tatsächlich vor sich geht. Noch wichtiger ist diese abgeleitete Formel:
Auf der linken Seite steht ein Ausdruck, der von der Masse des dritten Sterns abhängt (M3), dem Abstand zwischen dem dritten Stern und den beiden inneren (aout) und der Exzentrizität der Umlaufbahn des dritten Sterns um die beiden inneren (eout). Auf der rechten Seite steht ein Ausdruck, der von der Masse des Planeten (Mp), dessen Abstand von den beiden inneren Sternen (ap) und der Exzentrizität seiner Umlaufbahn (ep) abhängt. Die beiden Ausdrücke geben die Stärke der Gezeitenkräfte an, die vom äußeren Stern bzw. vom Planeten auf die beiden inneren Sterne wirken. Ist der Ausdruck auf der linken Seite der Gleichung größer, dann werden die Kozai-Zyklen unterdrückt. Im anderen Fall können sie wirken und die Bewegung der inneren Sterne entsprechend beeinflussen. Und wenn sie wirken, dann führt das dazu, dass der Abstand zwischen den beiden inneren Sternen schrumpft. Das ist der Mechanismus der “Kozai Cycle Tidal Friction” der in der Einleitung erwähnt worden ist und der für die Entstehung der engen Doppelsternsysteme verantwortlich gemacht wird!
Und nachdem jetzt die ganze Theorie der Bewegung von drei Sternen und einem Planet und alle wechselseitigen gravitativen Störungen und Resonanzen aufgearbeitet worden sind, geht es in Abschnitt 5 des Artikels endlich zur Sache: “EXPLAINING THE DEARTH OF PLANETS TRANSITING THE CLOSEST BINARIES”. Jetzt sind Martin und seine Kollegen also bereit zu erklären, warum es bei den engen Doppelsternen so wenig Planeten gibt!
Jetzt kommt also der eigentliche Hauptteil der Arbeit, also der Teil, bei dem man normalerweise einsteigen würde, wenn man einen normalen Artikel oder eine normale Pressemitteilung darüber schreiben wollen würde. Aber wenn ich das auch so gemacht hätte, hätten wir ja die ganze schöne Himmelsmechanik und Störungsrechnung aus dem Theorieteil verpasst! (Hat eigentlich überhaupt jemand bis hier her weiter gelesen? Wenn ja, dann sagt in den Kommentaren Bescheid und verwendet dabei als Beweis das Wort “Frischkäse”)
“In this section we develop an argument to explain the dearth of observed circumbinary planets transiting the closest binaries. To do so we determine regions where planets may be able to form and survive in evolving triple star systems. We first take a stable n-body orbit to be a necessary but probably not suffcient condition for planetary formation. We are therefore considering the most optimistic scenario possible.”
Martin und seine Kollegen verwenden nun jetzt also doch numerische Computersimulationen um die Bewegung eines Planeten in einem Dreifachsternsystem zu untersuchen. Die Theoriearbeit von vorhin wird aber trotzdem nicht umsonst gewesen sein! Vorerst aber geht darum nachzusehen, wo sich in so einem Dreifachsystem Regionen befinden, in der Planeten entstehen könnten.
Es geht mit einem Beispiel los:
Es wird also ein System betrachtet, bei dem sich zwei Sterne die jeweils so schwer wie die Sonne sind mit einer Periode von 100 Tagen umkreisen. Ein weiterer sonnenschwerer Stern umkreist diese beiden Sterne mit einer Periode von 338 Jahren (was einem Abstand von 70 Astronomischen Einheiten entspricht). Die Umlaufbahn des dritten Sterns ist kreisförmig und um 67 Grad gegenüber der Umlaufbahn der inneren Sterne geneigt (beide Werte sind zufällig gewählt bzw. würde das Beispiel mit anderen Werten genau so funktionieren). Das sollte – und um das herauszufinden braucht man jetzt die ganze vorher entwickelte Theorie! – zu einer Störung der Bahn der inneren Sterne führen so dass die sich auf einer stark exzentrischen Bahn bewegen und ihr Abstand schrumpft.
In diesem System befindet sich nun ein Planet der sich in der gleichen Ebene wie die beiden inneren Sterne außen um sie herum bewegt. Und wie wir dank der Theorie aus dem vorherigen Abschnitt wissen, hängt es von der Bahn und der Masse dieses Planeten ab, ob die Kozai-Störungen gedämpft werden oder nicht.
“For the 100 d binary there is a turnover at approximately ap = 6 AU. For smaller planetary semi-major axes we expect Kozai to be suppressed, because the circumbinary timescale is shorter than the Kozai timescale, and hence the planet maintains its circular, coplanar orbit. For farther out planetary orbits we expect the planet to undergo Kozai cycles and obtain an eccentricity ep;max = 0:86, leading to ejection.”
Aus den Gleichungen ergibt sich ein kritischer Abstand von ungefähr 6 Astronomischen Einheiten. Ist der Planet den beiden inneren Sternen näher als diese 6 AE, dann wird der Kozai-Effekt unterdrückt und die von den Sternen auf den Planet zurückwirkenden Störungen sind klein genug, damit er sich weiterhin auf seiner Bahn bewegen kann. Ist er weiter draußen, dann wird seine Bahn irgendwann so stark exzentrisch, dass er aus dem System raus fliegt.
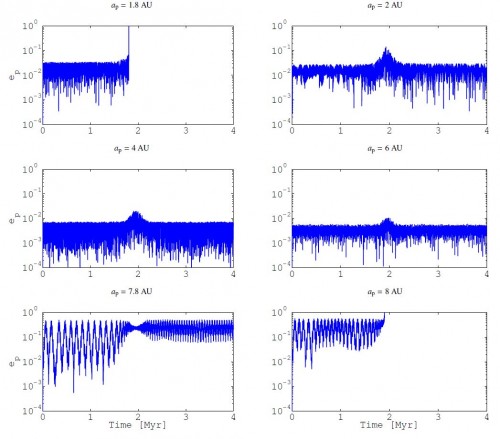
Soweit die (mathematisch angenäherte) Theorie. Die Realität der numerischen Simulationen sieht so aus:
Von oben links bis unten rechts sieht man, wie sich die Exzentrizität der Planetenbahn im Laufe von vier Millionen Jahren verändert, wenn der Planet 1.8, 2, 4, 6, 7.8 bzw. 8 Astronomische Einheiten von den inneren Sternen entfernt ist (Achtung, die Skala für die Exzentrizität ist nicht linear, sonder logarithmisch!). Je größer die Exzentrizität, desto langgestreckter ist die Planetenbahn und desto größer die Chance, dass er aus dem System fliegt. Oben links ist er den inneren Sternen zu nahe und die Bahn wird instabil. Ist er ein wenig weiter draußen, dann gibt es zwar kleinere Störungen (erkennbar am Ansteigen der Exzentrizität nach etwa 2 Millionen Jahren), aber die Bahn an sich bleibt stabil. Hinter der theoretischen Grenze von 6 AE wird die Veränderung der Exzentrizität schon erkennbar unregelmäßiger (und wenn man das Ding noch ein paar 100 Millionen Jahre länger simuliert würde ich wetten, dass die Bahn instabil wird!). Und bei 8 AE fliegt der Planet schließlich aus dem System.
Die anderen Bilder der Simulationsergebnisse erkläre ich jetzt nicht mehr im Detail, aber sie zeigen das gleiche Verhalten und demonstrieren, dass Theorie und Simulation im Rahmen des Erwartbaren gut übereinstimmen. Im nächsten Abschnitt erfolgt der nächste Vergleich zwischen Theorie und numerischer Simulation. Jetzt geht es um das, was in der “wichtigen” Formel von weiter oben behauptet wurde (die, in der es um den “Kozai Cycle Tidal Friction”-Mechanismus geht). Also um die Frage, bei welchen Eigenschaften eines Planeten der Kozai-Effekt unterdrückt wird oder nicht. Aus der Theorie folgt, dass ein Planet, der sich an der inneren Stabilitätsgrenze (die 2 AE Abstand die im Bild der Simulationsergebnisse von vorhin zu sehen sind) bewegt, höchstens 23 mal schwerer als die Erde sein kann, damit der Kozai-Effekt noch unterdrückt wird. Bewegt er sich an der äußeren Stabilitätsgrenze (7,8 AE), dann darf er dagegen 4,35 mal schwerer als Jupiter sein, bevor der KCTF-Mechanismus einsetzt.
Und wenn er einsetzt, dann schrumpft der Abstand zwischen den inneren Sternen. In unserem Beispiel verringert sich dadurch ihre Umlaufperiode von 100 Tagen auf 5 Tage. Das hat natürlich auch Auswirkungen auf die Stabilitätsgrenze für den Kozai-Effekt. Zuerst lag die – laut Theorie – bei 6 AE. Jetzt würde sie bei 2,5 AE liegen. Ich kann nur wiederholen: Himmelsmechanik kann verteufelt kompliziert werden! Andauernd ändert sich die Umlaufbahnen der Himmelskörper und immer wenn sie sich ändern, ändert sich auch die Art und Weise, mit der sie sich gegenseitig beeinflussen. Was wiederum dazu führt, dass sich die Umlaufbahnen verändern. Was zu veränderten gegenseitigen Störungen führt. Was zu veränderten Umlaufbahnen führt. Was zu… ich denke, ihr versteht, worum es geht! Dieses mathematische Problem ist ja nicht umsonst exakt unlösbar. Dieses ständige Hin und Her ist genau der Grund, warum es unlösbar ist (nicht, weil man noch nicht rausgefunden hat wie es geht – es ist prinzipiell unlösbar). Aber die Näherungen der Störungsrechnungen bieten zumindest einen kleinen Einblick auf das, was da alles abgeht und die numerischen Simulationen helfen dabei, die Gültigkeit der Theorie einzuschätzen.
Wie sich der KCTF-Mechanismus in Abhängigkeit von Stern- und Planetenparameter auswirkt und welche Auswirkungen das auf die Stabilität von Sternen und Planeten hat, haben Martin und seine Kollegen daher in numerischen Simulationen untersucht:
Zusammengefasst gesagt: Wenn der Abstand zwischen den inneren Sternen dank des KCTF-Mechanismus schrumpft, führt das dazu, dass die Bahn des Planeten tendenziell immer instabiler wird. Vom ursprünglichen Stabilitätsbereich zwischen 2 und 7,8 AE Abstand zu den inneren Sternen hat nur der allerinnerste Bereich (das innerste Sechstel) überlebt. Würden sich die beiden Sterne noch weiter annähern und ihre Umlaufzeit auf unter 5 Tage sinken, dann würde dieser letzte Rest des Stabilitätsbereich vermutlich komplett verschwinden. In so einem System könnten dann überhaupt keine Planeten mehr existieren (oder entstehen).
Apropos Entstehung: Der nächste Abschnitt geht auf ein paar Details der Planetenentstehung ein, die für diese Arbeit relevant sind:
“Our analysis so far has been limited to n-body orbital dynamics. However planets are believed to form in discs and only under certain favourable conditions. These necessary conditions further restrict the possible range of disc radii that can allow planet formation in a stellar triple system.”
Planeten entstehen ja aus großen Staub- und Gasscheiben, die einen Stern umgeben. Bei einem Einzelstern hängen die Ausmaße dieser Scheibe und damit die möglichen Regionen innerhalb der Scheibe die die nötigen Bedingungen für die Planetenentstehung bieten im Prinzip von der Masse der Gaswolke ab, aus denen der Stern entstanden ist. Je mehr Masse dort, desto mehr Masse kann auch die Scheibe haben. In Doppel- oder Mehrfachsternsystemen ist das aber anders, denn hier wird die Größe der Scheibe durch die gravitativen Störungen der anderen Sterne beschränkt.
Das wäre eigentlich wieder ein Thema für einen eigenen Artikel (bzw. ein eigenes Buch). Martin und seine Kollegen verweisen daher auch nur auf die einschlägige Literatur und fassen die dort gewonnenen Ergebnisse zusammen:
“The favoured theory is that planets are formed farther out in the disc in a more placid environment, before migrating inwards and halting near the inner truncation radius of the disc.
Da die Bedingungen in der Scheibe um einen Doppelsternsystem nahe der inneren Stabilitätsgrenze für die Planetenentstehung eher schlecht sind, geht man also davon aus, dass sie weiter draußen entstehen. Und dann durch planetare Migration weiter an den Doppelstern heran rücken. Was diese Migration ist und wie sie funktioniert habe ich hier ausführlich erklärt. Vereinfacht gesagt läuft es darauf hinaus, dass die entstehenden Planeten mit dem ganzen anderen Krempel in der Scheibe gravitativ wechselwirken und deswegen näher an den Stern rücken. So lange, bis das Ende der Scheibe erreicht ist. Und das ist auch offensichtlich der Grund, warum man Circumbinary Planeten vorrangig in der Nähe der Stabilitätsgrenze findet! Das war ja eine der Auffälligkeiten in den ursprünglichen Beobachtungsdaten, die zu Beginn des Artikels erwähnt worden sind.
Der Einfluss der planetaren Migration wird dann auch noch einmal extra im nächsten Abschnitt erläutert:
“Our analysis so far has only considered planets with static semi-major axes. However, as previously discussed, the favoured paradigm is that the circumbinary planets generally migrate inwards before being halted near the inner edge of the disc. The disc dispersal timescale (Alexander 2012) is expected to be much shorter than the KCTF timescale (Fabrycky & Tremaine 2007), and hence any migration will only occur around the primordial binary. This migration may have a positive or negative effect on planet survival, depending on the relative timescales of the inner binary Kozai cycles and disc migration. (…) If the planet migrates quickly and reaches the inner edge of the disc while the inner binary is still circular, then it will have migrated in too far and will be ejected once ein is subsequently excited during Kozai cycles. Alternatively, if the planet migrates slowly then the inner binary will have already undergone a full Kozai cycle and the disc will be truncated farther out, meaning that the planet will not get too close.”
Bis jetzt wurde in allen Rechnungen und Simulationen ja nur Planeten betrachtet, die nicht migriert sind. Wenn sie das aber tun, hat das natürlich auch wieder einen Einfluss auf die gesamte Dynamik! Je nachdem ob der Planet schnell oder langsam migriert, kann das einen negativen oder positiven Effekt auf seine Stabilität haben. Wenn er schneller migriert als die Zeitskale auf der der Kozai-Effekt abläuft, dann kommt er den beiden inneren Sternen schon zu einem Zeitpunkt nahe, wo die Kozai-Resonanz noch nicht lange genug gewirkt hat, um deren Bahnen exzentrisch zu machen. Und wenn das dann passiert, ist der Planet zu nahe dran, kriegt die dabei entstehenden gravitativen Störungen voll ab und fliegt aus dem System. Wenn er aber langsam migriert, dann hat der Kozai-Effekt die inneren Sterne schon lange auf exzentrische Bahnen gezwungen, bevor er dort ankommt. Die Störungen haben nun nicht auf den Planeten gewirkt, sondern auf die Scheibe mit dem ganzen Staub. Die wurde kleiner und weil der Planet nur in der Scheibe migrieren kann, kann er den beiden Sternen auch nicht naher kommen als deren innerer Rand. Seine Bahn schrumpft also nicht weit genug und der Abstand ist nach Ende der Migration immer noch ausreichend, damit er auf einer stabilen Bahn bleiben kann.

Zwei Sterne und ein Planet. Gibts im System Kepler-16. Aber anderswo sind solche Planeten selten (Künstlerische Darstellung: NASA/JPL-Caltech/R. Hurt)
Jetzt könnte man an dem Punkt angelangt sein, wo man den Überblick verloren hat (Wer liest noch mit? Das Codewort für die Kommentare lautet “Zahnpasta”!). Zum Glück kommt nun ein Abschnitt mit der Überschrift “The general picture”. Wie sieht das bisher gewonnene Bild der Dynamik von Planeten in engen Doppelsternsystemen also nun aus? Martin und seine Kollegen fassen die Lage in acht Punkten zusammen:
- Ein Planet entsteht um einen Doppelstern bei dem die Sterne weit voneinander entfernt sind. Ein weiter entfernter dritter Stern verursacht Kozai-Resonanzen, wodurch die Bahnen der inneren Sterne exzentrisch werden.
- Der Planet kann nur weit entfernt vom inneren Doppelstern existieren, da er ansonsten durch die stark exzentrischen Sternbahnen aus seiner Bahn geworfen würde.
- Der Planet kann aber auch nicht zu weit entfernt von den inneren Sternen sein. Denn nur so können die Störungen dieses dritten Sterns durch den Einfluss der inneren Sternen unterdrückt werden.
- Wenn der Planet ausreichend schwer und den inneren Sternen ausreichend nahe (aber immer noch im stabilen Bereich) ist, dann kann er selbst den Kozai-Effekt des dritten Sterns unterdrücken und damit verhindern, dass der Abstand zwischen den inneren Sternen schrumpft.
- Geht man davon aus, dass der Abstand schrumpft, dann werden einige Planetenbahnen im Laufe dieses Prozess instabil.
- Selbst in den stabilen Bereichen, wo der Einfluss der inneren Sternen die Störungen des dritten Sterns auf den Planeten unterdrücken, kann es immer noch zu leichten Störungen kommen, die dafür sorgen, dass die Bahn des Planeten sich gegenüber der Bahn der inneren Sterne neigt.
- Die Berücksichtigung der Bedingungen in der Scheibe in der Planeten entstehen führt zu weiteren Einschränkungen in der Stabilität der Planetenbahnen.
- Die Migration der Planeten kann dem Überleben der Planeten förderlich sein. Oder nicht.
Es gibt insgesamt nur einen kleinen Bereich, in dem ein Planet einerseits überleben und andererseits den KCTF-Mechanismus nicht unterdrücken kann. Und das heißt, dass die Chancen schlecht stehen, Planeten um enge Doppelsternsysteme zu finden, die durch den KCTF-Mechanismus entstanden sind. Und die Planeten, die überlebt haben, haben tendenziell Bahnen, auf denen wir sie mit der Transit-Methode nicht entdecken können:
“We conclude that most triple star systems evolving under KCTF are not conducive to hosting planets. Alternatively they host planets biased towards small masses, long periods and misaligned orbits, which are diffcult to detect via transits.”
Die ausführliche theoretische und numerische Untersuchung der Dynamik von Dreifachsternsystemen von Martin und seinen Kollegen hat also im Prinzip schon ausreichend demonstriert, warum man um enge Doppelsterne keine Planeten entdeckt hat. Im letzten Teil des Artikels erwähnen sie aber noch ein paar andere Punkte, die ebenfalls dazu führen, dass dort kaum Planeten entstehen oder überleben bzw. keine zu beobachten sind:
“Very close binaries are tidally locked, which increases the rotation speed and can lead to increased stellar activity. The standard Kepler 30-minute cadence may lead to insuffcient sampling at the shortest periods. And finally, Martin & Triaud (2015) calculated that some of the closest eclipsing binaries may be suffciently inclined with respect to our line of sight that transits by coplanar planets are not geometrically possible.”
Bei sehr engen Doppelsternen kann es zu erhöhter Sternaktivität kommen, was der Entstehung von Planeten nicht förderlich ist. Außerdem ist das Kepler-Weltraumteleskop nicht darauf ausgelegt, ausreichend schnelle Beobachtungen zu machen, um die Dynamik sehr enger Systeme aufzulösen bzw. können die dynamischen Effekte dazu führen, dass die Planeten sich nicht in der gleichen Bahnebene wie die Sterne befinden und daher nicht für uns sichtbar sind.
Sollte es bei engen Doppelsternen Planeten geben, dann braucht es andere Methoden, um sie zu entdecken. Die Autoren verweisen auf neue Weltraummissionen – zum Beispiel das PLATO-Teleskop des DLR – mit dem einige Entdeckungen möglich wären. Oder man benutzt die Gravitationslinsenmethode. Oder die Daten des GAIA-Teleskops. Wie üblich bei solchen Arbeiten stellt der letzte Satz fest, dass man neue Beobachtungen braucht, wenn man mehr wissen will:
“Continued observations, whether they reinforce this dearth or lead to surprising new discoveries, will allow this relatively new problem in exoplanetary physics to shed new light on a fundamental field of stellar physics.”
Egal, ob neue Beobachtungen das Fehlen der Planeten bei engen Doppelsternsystemen bestätigen oder “überraschende neue Entdeckungen” liefern: Man wird auf jeden Fall etwas Neues über das Verhalten von Sternen und Planeten lernen. Und genau darauf kommt es ja in der Wissenschaft an!
Ganz zu Schluss bedanken sich die Autoren dann noch bei ihren Kollegen, die sie bei der Arbeit unterstützt haben und bei den diversen Universitäten und Geldgebern. Und ich bedanke mich bei all den Leserinnen und Lesern, die tatsächlich bis zum Ende meines Artikels durchgehalten haben. Das wurde dann doch ein wenig länger, als ich es geplant hatte. Aber ich fand die Arbeit von Martin und seinen Kollegen wirklich interessant. Und auch wenn es anstrengend war, hat es doch Spaß gemacht, mich nach langer Zeit wieder einmal so richtig ausführlich mit einer himmelsmechanischen Facharbeit zu beschäftigen. Früher war das ja mein normaler Job, aber seit ich die universitäre Forschung verlassen habe, komme ich nicht mehr ganz so oft dazu.
Ich freue mich auf jeden Fall auf Feedback und wenn es nicht allzu negativ ausfällt, werde ich Ausschau nach einem neuen Artikel halten, denn ich irgendwann in Zukunft wieder so ausführlich besprechen kann.


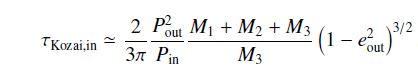
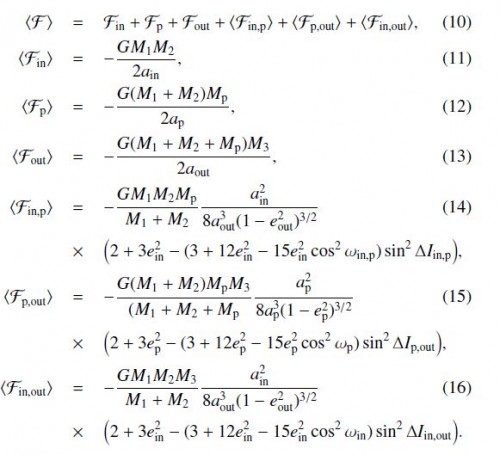

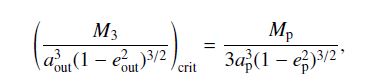












Kommentare (92)