Diese Störungen verursachen vor allem eine Veränderung der Exzentrizität in der Umlaufbahn der beiden inneren Sterne. Denn die beiden müssen einander ja nicht auf einer Kreisbahn umlaufen. Es kann genau so gut eine elliptische Bahn sein und wie stark die Umlaufbahn von einem Kreis abweicht, gibt die Exzentrizität an. Außerdem ändert sich durch die Störung der Winkel zwischen der Ebene in denen die beiden inneren Sterne einander umlaufen und der Ebene, in der sich der dritte Stern außen um beide herum bewegt.
Diese Störungen – die Variationen in der Exzentrizität und des Neigungswinkels der Bahnen – sind die weiter oben angesprochenen “Kozai Cycles” und die Zeitskala, auf der die Veränderungen stattfinden, werden durch diese Formel beschrieben:
Ich habe diese Formel hier nicht eingefügt, um sie im Detail zu erklären. Das würde viel zu weit führen. Aber man kann an ihr zumindest ein bisschen von der Methodik der Störungsrechnung erkennen. Eine exakte Lösung der Bewegung von mehreren Himmelskörpern ist ja wie gesagt nicht möglich. Aber in der Störungsrechnung arbeitet man mit Annäherungen: Man geht von einem lösbaren Fall aus (dem Zweikörperproblem) und fügt dann dieser exakten Lösung der Reihe nach kleinere Störungen hinzu, solange bis die gewünschte Genauigkeit erreicht ist. Dabei verwendet man mathematische Reihe, also im Allgemeinen unendlich lange Summen, bei denen jeder Term ein bisschen kleiner ist als der vorhergehende. Man kann diese unendliche Addition also irgendwo mitten drin abbrechen und trotzdem sicher sein, dass der Rest, den man ignoriert hat, nicht beliebig groß wird und der Fehler den man mit der Methode macht daher entsprechend klein bleibt. Ein typisches Zeichen für die Verwendung dieser mathematischen Reihen sind die Brüche (2/3) und Ausdrücke der Form (1-e²)3/2.
Nachdem die Autoren jetzt noch (ganz wichtig!) angegeben haben, mit welchem Softwarepaket sie all die numerischen Rechnungen durchgeführt haben, gehen sie im nächsten Abschnitt nochmal genauer auf die “Kozai Cycles” ein:
“Kozai cycles are the result of small perturbations induced by the tertiary star which build up coherently over the apsidal precession period. If there is an additional secular perturbation causing an apsidal precession of the binary on a shorter timescale, then the coherent eccentricity modulation is partially lost. Consequently, the amplitude of the tertiary’s perturbations decreases and the Kozai effect is suppressed. If the inner binary stars are close enough then apsidal precession due to general relativity and tidal and rotational bulges can suppress the Kozai modulation (Wu & Murray 2003; Fabrycky & Tremaine 2007). Alternatively, a suffciently close and massive circumbinary planet may also suppress the Kozai modulation”
Aber zuerst sollte ich nochmal kurz etwas allgemein zum Kozai-Zyklus beziehungsweise der Kozai-Resonanz sagen. Über himmelsmechanische Resonanzen habe ich ja früher schon einen ausführlichen Artikel geschrieben. Sie treten immer dann auf, wenn die Periode der Bewegung von zwei Himmelskörper in einem ganzzahligen Verhältnis zueinander steht. Wenn sich zum Beispiel ein Asteroid in der gleichen Zeit zweimal um die Sonne bewegt, in der der Jupiter eine Runde schafft, dann stehen sie in einer “2:1 Resonanz” der mittleren Bewegung. Dann können sich die gravitativen Störungen die Jupiter auf den Asteroid ausübt, im Laufe der Zeit aufschaukeln und dessen Bahn massiv verändern. Es gibt aber auch noch die sogenannten “säkularen Resonanzen”. Hier geht es nicht um die konkrete Bewegung der Himmelskörper selbst, sondern um die Veränderungen ihrer Bahn. So eine Umlaufbahn bleibt ja nicht konstant sondern ändert sich. Sie wird größer und kleiner, kreisförmiger und weniger kreisförmig und wackelt im Raum hin und her (das sind die sogenannten “Milankovic-Zyklen” über die ich hier gesprochen habe). Wenn jetzt zum Beispiel die Periode, mit der die Bahn eines Asteroiden im Raum hin und her wackelt in einem ganzzahligen Verhältnis zur Wackelperiode der Bahn des Jupiters steht, dann befinden sie sich in einer säkularen Resonanz, was ebenso zu großen Störungen führen kann.

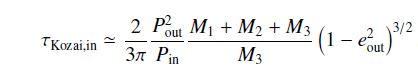










Kommentare (92)