Ein Spezialfall bei den Resonanzen ist jetzt aber die Kozai-Resonanz. Auch hier würde es viel zu weit führen, wenn ich diesen Effekt im Detail ableiten wollen würde. Es geht darum, dass die gravitativen Störungen zwischen den Himmelskörpern zwar (unter anderem) die Exzentrizität und die Neigung der Bahn verändern können, aber unter bestimmten Voraussetzungen eine Kombination dieser beiden Werte immer konstant bleiben muss (sie ist dann in diesem System eine Erhaltungsgröße wie die Energie oder der Drehimpuls). Das heißt nichts anderes als dass dann zum Beispiel die Exzentrizität der Bahn kleiner werden muss, wenn die Neigung der Bahn größer wird und umgekehrt. Dieses Auf-und-Ab sind die “Kozai Cycles” von denen im Artikel die Rede ist. Wie Martin und seine Kollegen aber anmerken, kann der Kozai-Effekt in ihrem Modell auch abgeschwächt werden, wenn verschiedene andere Resonanzen auf die richtige Art und Weise zusammenwirken. Beziehungsweise man die relativistischen Effekte der Bewegung oder Gezeitenkräfte im Modell berücksichtigt. Sogar die Störungen die ein Planet durch seine Gravitationskraft auf die Sterne ausübt, kann zu einer Abschwächung des Kozai-Effekts führen.
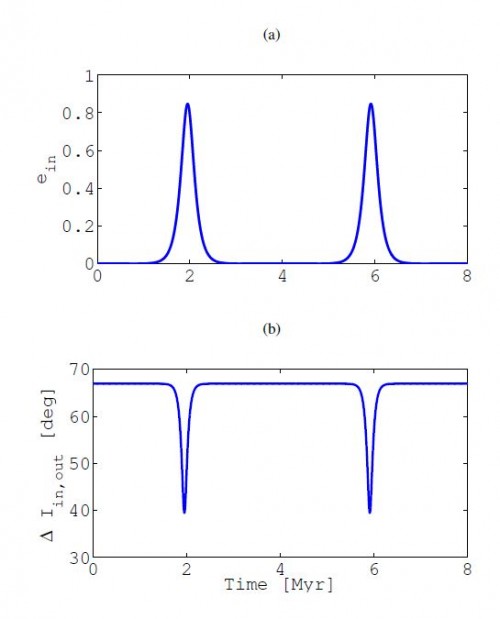
Beispiel für den Kozai-Effekt. Das obere Bild zeigt, wie sich die Exzentrizität der Umlaufbahn der beiden innern Sterne im Laufe von 8 Millionen Jahren ändert; das untere Bild zeigt die Veränderung der Bahnneigung in Bezug auf die Bahn des dritten Sterns. Die Änderungen laufen genau gegengleich ab (Bild: Martin et al, 2015)
Bevor Martin und seine Kollegen jetzt aber erklären, wozu sie den Kozai-Effekt in ihrer Arbeit überhaupt brauchen, gehen sie Abschnitt 4 des Artikels noch einmal im Detail auf die Bewegung von Planeten in Doppelsternsystemen ein. Sie beginnen wieder mit einer Definition:
“There are two possible planetary orbits in binary star systems:
(i) a circumbinary orbit around both stars or
(ii) a circumprimary orbit around one of the two stars”
Die finde ich persönlich ein wenig doof, weil das “circumprimary” missverständlich ist, wie die Autoren selbst in einer Fussnote anmerken: “Technically a circumprimary orbit only refers to when a planet orbits the bigger of the two stars and an orbit around the smaller star is a circumsecondary orbit, but for simplicity in this paper we will use the term circumprimary to refer to either case.”
Warum sie trotzdem auf diese Notation beharren und Planeten, die beide Sterne umlaufen “circumbinaries” nennen und Planeten die nur einen Stern umkreisen als “circumprimary” bezeichnen, kann ich nicht ganz nachvollziehen – vor allem weil ja auch die klarere “P-Typ” und “S-Typ” (was übrigens für “Planeten-Typ” und “Satelliten-Typ” steht) existiert. Aber ich bin da auch nicht objektiv, weil diese Definition von meiner ehemaligen Arbeitsgruppe in Wien eingeführt wurde. Und der Chef dieser Arbeitsgruppe wird auch im nächsten Absatz zitiert:
“There are restrictions on where a planet may orbit stably in a binary star system, primarily as a function of the binary’s semi-major axis (e.g., Dvorak 1986; Holman & Wiegert 1999). Planets orbiting on the wrong side of the stability limit are generally ejected from the system by a process of resonance overlap”
Hier beziehen sich Martin und seine Kollegen auf die frühen theoretischen Arbeiten, bei denen berechnet wurde, wo sich bei Doppelsternen stabile Bahnen für Planeten befinden. Die erste dieser Arbeiten stammt von Rudolf Dvorak, mein ehemaliger Chef und Doktorvater. Ich finde es heute immer noch bemerkenswert, dass er schon 1986 untersucht hat, wo es bei Doppelsterne stabile Bahnen für Planeten gibt, obwohl damals noch kein einziger extrasolarer Planet entdeckt worden war. In Arbeiten die sich mit Planeten bei Doppelsternen beschäftigen wird aber meistens auf die spätere Arbeit von Holman & Wiegert aus dem Jahr 1999 verwiesen, die mit den dann schon viel besseren Computern auch genauere Rechnungen durchführen konnten und die Stabilitätsgrenzen genauer bestimmen konnten. Wie diese Grenze berechnet wird, zeigt die nächste Formel im Artikel, die ich jetzt aber nicht im Detail erklären werde. Es reicht zu wissen, dass der Abstand der Grenze vom Doppelstern von drei Größen abhängt: Dem Verhältnis der Sternmassen, dem Abstand der Sterne und der Exzentrizität ihrer Umlaufbahn.











Kommentare (92)