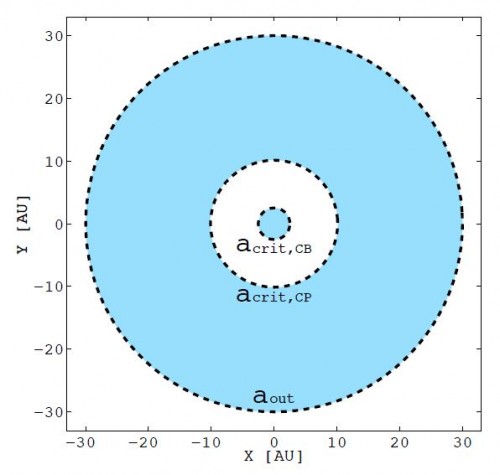
Im nächsten Abschnitt geht es um die “säkulare Entwicklung” der Umlaufbahnen der Sterne umeinander. Genauer gesagt um die “nodal and apsidal precession”. Damit ist die Drehung der Bahn um zwei der drei Richtungen im Raum gemeint (der dritte mögliche Drehwinkel wäre die Bahneigung). In der Arbeit von Martin und seinen Kollegen geht es aber ja um Planeten, die sich in Dreifachsternsystemen befinden und das ist der Thema von Abschnitt 4.2. Hier wird es knifflig. Erinnern wir uns das Modell mit den beiden entkoppelten Doppelsternen (der eine reale, mit den inneren Sternen und der zweite mit dem dritten und dem “fiktiven” Stern). Der Planet ist in Bezug auf die beiden inneren Sterne ein “circumbinary” (p-Typ). In Bezug auf das Doppelsternsystem mit dem äußeren dritten Stern ist er aber ein “circumprimary” (s-Typ) weil er ja den fiktiven Stern (bestehend aus den beiden inneren Sternen) umkreist. Will man etwas über die Stabilität der Bewegung des Planeten wissen, dann muss man die Stabilitätsgrenzen für beide Fälle berücksichtigen. Damit man sich das besser vorstellen kann, bringen die Autoren ein Beispiel für ein Dreifachsternsystem, bei die inneren beiden Sterne 0,5 Astronomische Einheiten (1 AE = 150 Millionen Kilometer) voneinander entfernt sind und der äußere dritte Stern 30 AE von den beiden inneren entfernt ist:
Alles was in diesem Bild blau ist, ist instabil. Ein Planet könnte dort nicht existieren, sondern würde mit einem der Sterne kollidieren oder aus dem System rausfliegen. Nur wenn weit genug vom dritten Stern entfernt und gleichzeitig den beiden inneren Sternen nicht zu nahe ist, also im weißen Bereich in der Mitte des Bildes, kann er sich auf einer stabilen Bahn bewegen. Aber auch wenn er sich in der stabilen Region befindet, heißt das nicht, dass der Planet keinen Störungen ausgesetzt ist – es sind eben nur Störungen, die normalerweise nicht allzu groß werden und sich nur innerhalb gewisser Grenzen auswirken können. Die Astronomen schreiben:
“A planet orbiting within the stability region of a misaligned triple star system is perturbed by two competing secular effects: precession due to the inner binary and Kozai cycles due to the outer binary”
Von den beiden inneren Sternen wird die Bahn des Planeten also auf eine Weise gestört, die zu einer kontinuierlichen Drehung der Bahn führt (“precession”); der dritte äußere Stern erzeugt die oben beschriebene Kozai-Resonanz und lässt Bahnneigung und Exzentrizität der Planetenbahn variieren. Wie sich diese beiden Störungen konkret auswirken, hängt vom Spezialfall ab. Weiter oben habe ich ja erwähnt, dass der Kozai-Effekt auch unterdrückt werden kann. Und das ist näherungsweise dann der Fall, wenn die Störungen durch die inneren Sterne mit einer langsameren Periode stattfinden als die Kozai-Zyklen die vom dritten Stern ausgelöst werden. Um ein vollständiges Bild der Dynamik zu erhalten, muss man jetzt noch untersuchen, wie sich die gravitativen Störungen des Planeten auf die Bewegung der Sterne auswirken. Denn die bestimmt ja wiederum die Störung, die auf den Planeten wirkt (Hey, niemand hat behauptet, Himmelsmechanik wäre nicht knifflig!). Und um das zu berechnen, muss man jetzt wirklich ganz tief in die mathematische Trickkiste der Störungsrechnung greifen! Das kann ich hier schlicht und einfach nicht erklären (denn dann müsste ich wirklich ein Buch schreiben und dieses Buch steht ja auf der Liste der Dinge die ich gerne machen würde aber nicht machen werde). Ich zeige euch nur, wie so etwas aussieht:
Die Funktion “F” ganz oben in dieser Liste ist die Hamilton-Funktion die im Prinzip die Energie beschreibt, die im ganzen System steckt. Kennt man die Hamilton-Funktion kann man damit die Gleichungen aufstellen, die beschreiben, wie sich alles bewegt. Um diese Funktion aufstellen zu können, muss man sich aber meistens mit Annäherungen begnügen, die durch Störungsrechnung gefunden werden können und wie die in diesem Fall aussehen, zeigen die restlichen Funktionen in der Liste. Diese Rechnungen anzustellen ist alles andere als trivial und wirklich nur etwas für ganz begeisterte Himmelsmechaniker. Martin und seine Kollegen haben auch verzichtet, die ganze dahinter stehende Mathematik im Detail aufzulisten und einfach auf die entsprechende Literatur verwiesen (was dann bei den Kollegen für große Begeisterung sorgt, die das ganze nachrechnen müssen, wenn sie die Arbeit tatsächlich komplett nachvollziehen wollen).

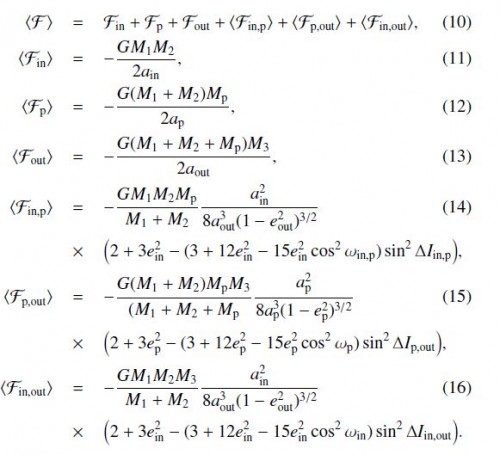










Kommentare (92)