Die Arbeit müsste man sich eigentlich nicht antun. Heutzutage hat man ja schnelle Computer und könnte das ganze Problem ganz einfach numerisch am Computer simulieren. Das geht – je nach Methode – mit fast beliebiger Genauigkeit und man würde sich die ganzen mühsamen Rechnungen sparen und könnte gleichzeitig auf die mathematischen Näherungen verzichten sondern wirklich alle dynamischen Effekte inkludieren. Der Nachteil an diesem Simulationsansatz ist aber, dass man dann keine Ahnung, wie sich die dynamischen Effekte im Detail auswirken und welche Rolle welcher Effekt spielt. In so eine Simulation steckt man den Ort der Himmelskörper hinein und bekommt den Ort der Himmelskörper heraus, den sie zu einem späteren Zeitpunkt einnehmen. Das ist in vielen Fällen enorm nützlich. Aber eben nicht immer. Denn wenn man es geschafft hat, sich eine Hamilton-Funktion zu basteln, dann kann man die auch analysieren. So zum Beispiel:
Hier haben Martin und seine Kollegen aus der Hamilton-Funktion eine Formel (20) abgeleitet, die angibt, wie sich die Exzentrizität der Umlaufbahn der beiden inneren Sterne in Abhängigkeit der Neigung zwischen der Bahnebene des äußeren dritten Sterns und der Bahnebene der inneren Sterne verändert. So etwas ist enorm wertvoll, wenn man verstehen will, was in solchen Systemen tatsächlich vor sich geht. Noch wichtiger ist diese abgeleitete Formel:
Auf der linken Seite steht ein Ausdruck, der von der Masse des dritten Sterns abhängt (M3), dem Abstand zwischen dem dritten Stern und den beiden inneren (aout) und der Exzentrizität der Umlaufbahn des dritten Sterns um die beiden inneren (eout). Auf der rechten Seite steht ein Ausdruck, der von der Masse des Planeten (Mp), dessen Abstand von den beiden inneren Sternen (ap) und der Exzentrizität seiner Umlaufbahn (ep) abhängt. Die beiden Ausdrücke geben die Stärke der Gezeitenkräfte an, die vom äußeren Stern bzw. vom Planeten auf die beiden inneren Sterne wirken. Ist der Ausdruck auf der linken Seite der Gleichung größer, dann werden die Kozai-Zyklen unterdrückt. Im anderen Fall können sie wirken und die Bewegung der inneren Sterne entsprechend beeinflussen. Und wenn sie wirken, dann führt das dazu, dass der Abstand zwischen den beiden inneren Sternen schrumpft. Das ist der Mechanismus der “Kozai Cycle Tidal Friction” der in der Einleitung erwähnt worden ist und der für die Entstehung der engen Doppelsternsysteme verantwortlich gemacht wird!
Und nachdem jetzt die ganze Theorie der Bewegung von drei Sternen und einem Planet und alle wechselseitigen gravitativen Störungen und Resonanzen aufgearbeitet worden sind, geht es in Abschnitt 5 des Artikels endlich zur Sache: “EXPLAINING THE DEARTH OF PLANETS TRANSITING THE CLOSEST BINARIES”. Jetzt sind Martin und seine Kollegen also bereit zu erklären, warum es bei den engen Doppelsternen so wenig Planeten gibt!
Jetzt kommt also der eigentliche Hauptteil der Arbeit, also der Teil, bei dem man normalerweise einsteigen würde, wenn man einen normalen Artikel oder eine normale Pressemitteilung darüber schreiben wollen würde. Aber wenn ich das auch so gemacht hätte, hätten wir ja die ganze schöne Himmelsmechanik und Störungsrechnung aus dem Theorieteil verpasst! (Hat eigentlich überhaupt jemand bis hier her weiter gelesen? Wenn ja, dann sagt in den Kommentaren Bescheid und verwendet dabei als Beweis das Wort “Frischkäse”)
“In this section we develop an argument to explain the dearth of observed circumbinary planets transiting the closest binaries. To do so we determine regions where planets may be able to form and survive in evolving triple star systems. We first take a stable n-body orbit to be a necessary but probably not suffcient condition for planetary formation. We are therefore considering the most optimistic scenario possible.”
Martin und seine Kollegen verwenden nun jetzt also doch numerische Computersimulationen um die Bewegung eines Planeten in einem Dreifachsternsystem zu untersuchen. Die Theoriearbeit von vorhin wird aber trotzdem nicht umsonst gewesen sein! Vorerst aber geht darum nachzusehen, wo sich in so einem Dreifachsystem Regionen befinden, in der Planeten entstehen könnten.


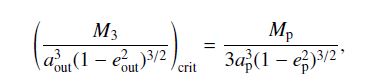










Kommentare (92)