Es geht mit einem Beispiel los:
Es wird also ein System betrachtet, bei dem sich zwei Sterne die jeweils so schwer wie die Sonne sind mit einer Periode von 100 Tagen umkreisen. Ein weiterer sonnenschwerer Stern umkreist diese beiden Sterne mit einer Periode von 338 Jahren (was einem Abstand von 70 Astronomischen Einheiten entspricht). Die Umlaufbahn des dritten Sterns ist kreisförmig und um 67 Grad gegenüber der Umlaufbahn der inneren Sterne geneigt (beide Werte sind zufällig gewählt bzw. würde das Beispiel mit anderen Werten genau so funktionieren). Das sollte – und um das herauszufinden braucht man jetzt die ganze vorher entwickelte Theorie! – zu einer Störung der Bahn der inneren Sterne führen so dass die sich auf einer stark exzentrischen Bahn bewegen und ihr Abstand schrumpft.
In diesem System befindet sich nun ein Planet der sich in der gleichen Ebene wie die beiden inneren Sterne außen um sie herum bewegt. Und wie wir dank der Theorie aus dem vorherigen Abschnitt wissen, hängt es von der Bahn und der Masse dieses Planeten ab, ob die Kozai-Störungen gedämpft werden oder nicht.
“For the 100 d binary there is a turnover at approximately ap = 6 AU. For smaller planetary semi-major axes we expect Kozai to be suppressed, because the circumbinary timescale is shorter than the Kozai timescale, and hence the planet maintains its circular, coplanar orbit. For farther out planetary orbits we expect the planet to undergo Kozai cycles and obtain an eccentricity ep;max = 0:86, leading to ejection.”
Aus den Gleichungen ergibt sich ein kritischer Abstand von ungefähr 6 Astronomischen Einheiten. Ist der Planet den beiden inneren Sternen näher als diese 6 AE, dann wird der Kozai-Effekt unterdrückt und die von den Sternen auf den Planet zurückwirkenden Störungen sind klein genug, damit er sich weiterhin auf seiner Bahn bewegen kann. Ist er weiter draußen, dann wird seine Bahn irgendwann so stark exzentrisch, dass er aus dem System raus fliegt.
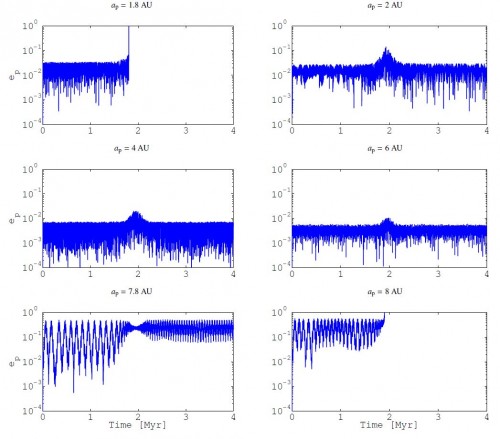
Soweit die (mathematisch angenäherte) Theorie. Die Realität der numerischen Simulationen sieht so aus:
Von oben links bis unten rechts sieht man, wie sich die Exzentrizität der Planetenbahn im Laufe von vier Millionen Jahren verändert, wenn der Planet 1.8, 2, 4, 6, 7.8 bzw. 8 Astronomische Einheiten von den inneren Sternen entfernt ist (Achtung, die Skala für die Exzentrizität ist nicht linear, sonder logarithmisch!). Je größer die Exzentrizität, desto langgestreckter ist die Planetenbahn und desto größer die Chance, dass er aus dem System fliegt. Oben links ist er den inneren Sternen zu nahe und die Bahn wird instabil. Ist er ein wenig weiter draußen, dann gibt es zwar kleinere Störungen (erkennbar am Ansteigen der Exzentrizität nach etwa 2 Millionen Jahren), aber die Bahn an sich bleibt stabil. Hinter der theoretischen Grenze von 6 AE wird die Veränderung der Exzentrizität schon erkennbar unregelmäßiger (und wenn man das Ding noch ein paar 100 Millionen Jahre länger simuliert würde ich wetten, dass die Bahn instabil wird!). Und bei 8 AE fliegt der Planet schließlich aus dem System.
Die anderen Bilder der Simulationsergebnisse erkläre ich jetzt nicht mehr im Detail, aber sie zeigen das gleiche Verhalten und demonstrieren, dass Theorie und Simulation im Rahmen des Erwartbaren gut übereinstimmen. Im nächsten Abschnitt erfolgt der nächste Vergleich zwischen Theorie und numerischer Simulation. Jetzt geht es um das, was in der “wichtigen” Formel von weiter oben behauptet wurde (die, in der es um den “Kozai Cycle Tidal Friction”-Mechanismus geht). Also um die Frage, bei welchen Eigenschaften eines Planeten der Kozai-Effekt unterdrückt wird oder nicht. Aus der Theorie folgt, dass ein Planet, der sich an der inneren Stabilitätsgrenze (die 2 AE Abstand die im Bild der Simulationsergebnisse von vorhin zu sehen sind) bewegt, höchstens 23 mal schwerer als die Erde sein kann, damit der Kozai-Effekt noch unterdrückt wird. Bewegt er sich an der äußeren Stabilitätsgrenze (7,8 AE), dann darf er dagegen 4,35 mal schwerer als Jupiter sein, bevor der KCTF-Mechanismus einsetzt.












Kommentare (92)