In den letzten Jahren haben Astronomen viele Planeten bei anderen Sternen entdeckt und darunter auch viele sehr junge Systeme, bei denen die Himmelskörper gerade erst entstanden sind. Wir kennen außerdem viele sogenannte protoplanetare Scheiben: große Mengen an Staub und Gas die einen Stern umgeben und aus denen später einmal Planeten entstehen. Was man bis jetzt allerdings noch nicht beobachten konnte, ist das, was dazwischen passiert. Der Staub klumpt im Laufe der Zeit zu größeren Brocken zusammen, den Planetesimalen die wiederum selbst miteinander kollidieren und dabei am Ende große Planeten formen. So lautet zumindest die Theorie, denn gesehen hat diesen Vorgang bis jetzt noch niemand. Astronomen von der Universität Bristol haben nun überlegt, wie man das ändern könnte.
Es gibt mehrere Gründe, warum man den kritischen Schritt bei der Entstehung von Planeten so schwer beobachten kann. Staub zum Beispiel ist zwar klein, hat aber im Verhältnis zu seiner Masse (insgesamt) eine sehr große Oberfläche. Staub wird durch die Strahlung des Sterns aufgeheizt und gibt die Strahlung in Form von Wärme wieder ab und das lässt sich sehr gut beobachten. Planeten haben im Verhältnis zu ihrer Masse nur eine sehr kleine Oberfläche und leuchten selbst nicht; sind aber eben massereich genug um ihren Stern gravitativ zu beeinflussen was sich ebenfalls beobachten lässt. Aber die meter- bzw. kilometergroßen Felsbrocken, die Planetesimale die aus dem Staub entstanden sind und aus denen die Planeten entstehen sind weder massereich genug um irgendwelche beobachtbaren Auswirkungen beim Stern zu verursachen, noch ist ihre Oberfläche ausreichend um genug detektierbare Strahlung abzugeben. Und haben sich daher bis jetzt der Beobachtung immer erfolgreich entzogen.
Dieses Bild, das vom großen Radioteleskop ALMA aufgenommen worden ist, zeigt eine protoplanetare Scheibe um den Stern HL Tauri:
Man sieht das Leuchten des Staubs, aber auch dunkle Stellen in der Scheibe, die darauf hinweisen, dass sich hier schon größere Planeten gebildet haben. Mit ihrer Gravitationskraft räumen sie den Staub entlang ihrer Umlaufbahn aus dem Weg und bald wird sich die protoplanetare Scheibe ganz aufgelöst haben. Den Zwischenschritt der eigentlichen Planetenentstehung hat man hier schon verpasst – aber in Zukunft könnte ALMA anderswo erfolgreicher mit der Beobachtung sein.
Das ist das Resultat einer Arbeit von Zoë Leinhardt von der Universität Bristol und ihrer Kollegen (“Numerically Predicted Indirect Signatures of Terrestrial Planet Formation”). Sie haben sich überlegt, dass man zwar die Planetesimale nicht direkt beobachten kann, aber vielleicht die Auswirkungen dessen, was sie tun wenn sich Planeten bilden. Das geschieht dem aktuellen Modell der Planetenentstehung zufolge durch Kollisionen. Planetesimale stoßen zusammen und verschmelzen dabei zu immer größeren Körpern. Und wenn sie das tun, entsteht dabei neuer Staub. Staub, der sich unter Umständen beobachten lässt.
Um herauszufinden, wie sich der Staub bei der Entstehung erdähnlicher Planeten (das heißt Planeten mit ungefähr der gleichen Größe und Masse der Erde) verhält, haben Leinhardt und ihre Kollegen den ganzen Prozess am Computer simuliert. Das ist nicht ganz so einfach, wie eine reine Simulation der Bewegung von Himmelskörpern. Denn hier müssen auch die Kollisionen und ihr Ergebnis berücksichtigt werden. Je nachdem mit welcher Geschwindigkeit die Planetesimale kollidieren und welche Größe und Masse sie haben, entstehen am Ende dabei mehr oder weniger große Objekte und mehr oder weniger Staub.
Die Simulation von Leinhardt und ihren Kollegen begann mit einem Ring aus Planetesimalen der sich in einem Abstand von 0,5 bis 1,5 Astronomischen Einheiten um einen sonnenähnlichen Stern erstreckt. Eine Astronomische Einheit entspricht dem mittleren Abstand der Erde von der Sonne und der Ring aus Planetesimalen würde sich also in unser Sonnensystem versetzt in etwa zwischen den Bahnen von Venus und Mars befinden. Die Gesamtmasse aller Planetesimale im Ring beträgt 2,8 Erdmassen und ihre Größe ist entsprechend den üblichen Modellen der Planetenentstehung verteilt.
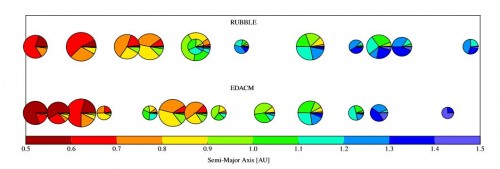
Am Computer haben Leinhardt und ihre Kollegen nun nachgesehen, was im Laufe der Zeit mit diesen Planetesimalen passiert und was aus ihnen entsteht. Das hier zum Beispiel:
Dieses Bild zeigt die am Ende der Simulation entstandenen jungen Planeten. Sie sind mit ihrem jeweiligen Abstand vom Stern aufgereiht (der auf der x-Achse in Astronomischen Einheiten angegeben ist). Die beiden Reihen entsprechen zwei leicht unterschiedlichen Computermodellen für das Verhalten der Planetesimale bei Kollisionen. Jeder Planet ist als Tortengrafik gezeichnet, in der angegeben ist, wie viel Material aus welchem Bereich des ursprünglichen Rings zu seiner Entstehung beigetragen hat, was durch die Farbe gekennzeichnet ist. Logischerweise enthalten sternnahe Planeten hauptsächlich ursprünglich sternnahes Material und sternferne Planeten sternfernes Material. Aber es kommt durchaus aus zu Mischungen, besonders im Bereich dazwischen, also der Region, in der sich um einen sonnenähnlichen Stern auch die sogenannte habitable Zone befindet (die Region, in der es nicht zu heiß und nicht zu kalt für die Entstehung von Leben ist). Wenn Material aus unterschiedlichen Regionen der Scheibe miteinander kollidiert hat das auch sehr spezielle Auswirkungen auf die Produktion von Staub. Die Geschwindigkeit der Planetesimale ändert sich, je nachdem ob sie den Stern nah oder fern umkreisen und auch ihre Menge hängt vom Abstand ab.
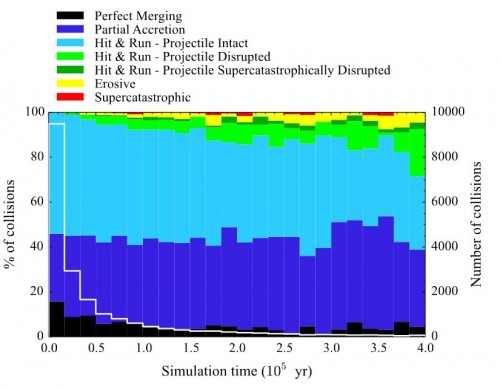
Welche unterschiedlichen Kollisionsarten bei der Entstehung der Planeten eine Rolle spielen, zeigt diese Grafik:
Man sieht hier auf der x-Achse die simulierte Zeit die während den Kollisionen vergangen ist (insgesamt 400.000 Jahre). Für jedes Zeitintervall gibt ein Balkendiagramm an, welche Kollisionsarten wie oft vorgekommen sind, was durch die Farben gekennzeichnet ist. Schwarze Balken bedeuten zum Beispiel eine komplette Verschmelzung der beiden kollidierenden Planetesimale. Dunkelblau sind Kollisionen, bei denen es nur zu einer teilweisen Verschmelzung kam und hellblaue Balken geben Zusammenstöße an, bei denen ein Objekt wesentlich schneller unterwegs war als das andere und bei der Kollision intakt blieb während das andere Objekt zerstört wurde. Grüne, gelbe oder rote Balken zeigen noch heftigere Kollisionen bei denen noch mehr Staub entsteht. Die weiße Linie, die sich durch das Diagramm zieht zeigt an, wie viele Kollisionen es insgesamt gab.
Man sieht recht deutlich, dass die Kollisionen im Laufe der Zeit schnell abnehmen. Aber das ist auch logisch: Je mehr Material vorhanden ist, desto mehr Kollisionen gibt es und je mehr Kollisionen es gibt, desto schneller verschwinden die Planetesimale die kollidieren können und werden zu größeren Planeten. Man sieht aber auch, dass die Zahl der perfekten Verschmelzungen im Laufe der Zeit sinkt während die stark staubproduzierenden heftigen Kollisionen gegen Ende der Simulation zunehmen.
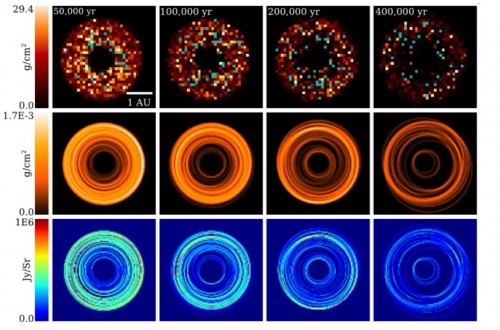
Leinhardt und ihre Kollegen waren aber ja eigentlich nicht so sehr an den großen Endprodukten der Planetenentstehung interessiert, sondern an dem, was dabei übrig bleibt: Dem Staub. Und haben daher auch genau beobachtet, wo und wie sich die ganzen Trümmer der Kollisionen auf- und verhalten. Aus diesen Daten haben sie ein entsprechendes Modell erstellt, das zeigt wie viel Staub sich während der Entstehung der Planeten in einem bestimmten Abstand vom Stern befinden muss. Aber das ist nur der erste Schritt, denn man muss nun auch noch berechnen, auf welche Art dieser Staub Licht des Sterns absorbiert, abstrahlt oder reflektiert, denn das ist es ja, was man am Ende beobachten kann. So sehen die Resultate aus:
Die oberste Reihe des Diagramms zeigt die Dichteverteilung der Planetesimale zu verschiedenen Zeitpunkten während der simulierten Planetenentstehung. Man sieht schön, wie die Scheibe im Laufe der Zeit (also von links nach rechts) immer “klumpiger” wird, da sich aus den vielen kleinen Planetesimalen am Anfang der Simulation wenige große Planeten am Ende bilden. In der zweiten Reihe ist die Dichteverteilung des bei diesem Prozess entstehenden Staubs abgebildet. Und die dritte Reihe zeigt schließlich genau das, was ein Teleskop wie ALMA beobachten könnte, würde es auf in dieser Art verteilten Staub blicken.
Die unterste Reihe des Diagramms besteht also aus simulierten Teleskopbildern und stellt damit auch eine überprüfbare Vorhersage dar. Sie auch tatsächlich zu überprüfen wird allerdings vorerst noch schwer werden. Die abgestrahlte Energie ist zu schwach, um sie selbst mit einem großen Teleskop wie ALMA in einer vernünftigen Zeit beobachten zu können. Man bräuchte dafür absurd lange Belichtungszeiten von mehreren hundert Jahren und das ist natürlich nicht praktikabel. Aber wenn man das ganze Problem entsprechend skaliert und sich auf Sterne konzentriert, deren protoplanetare Scheiben sehr viel mehr Masse enthalten, dann könnte es gehen. Und das ist nicht unwahrscheinlich: Die Masse der Scheibe auf der die Simulationen von Leinhardts Team beruhen war vergleichsweise gering und vermutlich sogar geringer als die, aus der die Planeten unserer Sonne entstanden sind. Andere Sterne können durchaus sehr viel größere Scheiben haben. Und die könnten in den nächsten Jahren tatsächlich mit ALMA detektiert werden. Es liegt jetzt also bei den Beobachtern, die Vorhersagen ihrer Kollegen zu überprüfen…












Kommentare (54)