Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2016. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier.

Das sagt der Autor des Artikels, Andreas Geyer-Schulz über sich:

Andreas Geyer-Schulz ist wissenschaftlicher Mitarbeiter am Karlsruher
Institut für Technologie.
Im Rahmen des Sonderforschungsbereichs „Wellenphänomene“ (SFB 1173)
beschäftigt er sich mit dispersiven Differentialgleichungen.
Weitere Informationen über die Tätigkeiten des SFB finden Sie im
SFB-Blog.

——————————————

Was machen eigentlich Mathematiker?

We often hear that mathematics consists mainly of “proving theorems”.
Is a writer’s job mainly that of “writing sentences”? — Gian-Carlo Rota

Prolog

In der Schule kommt Mathematik kaum vor.
Daher ist es wenig verwunderlich, dass viele Leute keine Vorstellung davon haben, was Mathematiker eigentlich machen.
Aber auch für Mathematiker ist es gar nicht so leicht, Fachfremden Einblicke in ihre Tätigkeit zu geben.

Mathematiker erzählen sehr gerne über ihre Arbeit.
Jedoch stoßen sie schnell auf Schwierigkeiten sich verständlich auszudrücken.
Ein Beispiel: In der ersten Version dieses Artikels habe ich den Begriff „bijektive Abbildung“ verwendet.
Tatsächlich ist das Wort „bijektiv“ den meisten Menschen unbekannt.
Auch das Wort „Abbildung“ hat im Alltag eine andere Bedeutung als in der Mathematik.

Nun ist es nicht schlimm, wenn man das Wort „bijektiv“ nicht kennt.
Es wäre auch nicht schwer zu verstehen, was es bedeutet.
Jedoch gibt es in der Mathematik viele Fachwörter, die eine ganz präzise Bedeutung haben.
Hieraus ergibt sich ein Problem, wenn ein Mathematiker zur Allgemeinheit spricht.
Wenn er begeistert anfängt über ein mathematisches Thema zu reden und dabei nicht ins Vage und Ungefähre abdriften möchte, so stellt er fest, dass er erst einmal viele Wörter und ihre Bedeutung erklären müsste.
Und vor lauter Wörter Erklären kommt er dann gar nicht mehr dazu von der Mathematik zu erzählen.

Um dieses Problem zu vermeiden schreibe ich nicht über „ernsthafte“, „nützliche“ oder gar „berühmte“ Mathematik.
Sondern ich schreibe über ein Beispiel, hinter dem sich technisch und begrifflich einfache Mathematik verbirgt.
Trotz dieser Einfachheit zeige ich daran exemplarisch typische Vorgehensweisen von Mathematikern.
Insbesondere gehe ich auf die folgenden Punkte ein.

• Wie kann man reale Vorgänge in der Sprache der Mathematik beschreiben?
• Für welche Fragestellungen interessieren sich Mathematiker?
• Wie gelangen sie zu neuen Erkenntnissen?
• Welchen Nutzen hat Mathematik?

Betrachten wir dazu das Video eines Jongleurs.

Teil 1. Mathematiker erfinden eigene Sprachen

Mathematiker arbeiten mit abstrakten Objekten, die keine direkte Entsprechung in der realen Welt besitzen, zum Beispiel Zahlen, Mengen, Funktionen …
Umgekehrt ist ein Jongleur kein mathematisches Objekt.
Es geht nun darum, das Jonglieren in der realen Welt durch ein mathematischen Modell zu beschreiben.
Erst innerhalb eines solchen Modells kann ein Mathematiker Mathematik betreiben.
Wesentliche Eigenschaften sollen in einem sinnvollen Modell erhalten bleiben, unwesentliche werden ignoriert.
Was ist also im obigen Video wesentlich um die Jonglage zu verstehen?

Durch genaue Beobachtung des Videos stellt man fest.

1. Zu einem gewissen Zeitpunkt wird je ein Ball gefangen und gleich wieder geworfen.
2. Zwischen den Würfen vergeht in etwa gleich viel Zeit.
3. Es wird abwechselnd mit der linken und der rechten Hand geworfen.
4. Die Bälle werden unterschiedlich hoch geworfen.
5. Die Reihenfolge, in der die Bälle geworfen werden, ändert sich.

Diese Beobachtungen führen zu einem mathematischen Modell.
Aus der Sicht eines Jongleurs spielen nur die Zeitpunkte eine Rolle, in denen er in das Geschehen eingreift.
Dies ist der Moment, in dem er einen Ball fängt und von neuem in die Luft wirft.
Dazwischen fliegen die Bälle von ganz alleine gemäß der physikalischen Gesetze, die im Folgenden keine Rolle spielen.
Was muss der Jongleur im Moment des Abwurfs wissen?
Er muss so hoch werfen, dass der Ball zum richtigen Zeitpunkt wieder landet.
Der richtige Zeitpunkt ist dabei durch das gewünschte Jongliermuster bestimmt.
Im einfachsten Fall landen die Bälle wieder in der Reihenfolge, in der sie geworfen wurden.
Aber auch kompliziertere Muster sind möglich.

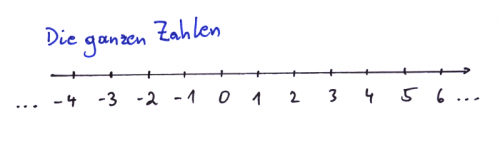
Als Modell für die Zeitpunkte des Werfens verwenden wir die ganzen Zahlen ...,-3,-2,-1,0,1,2,3,....

Wir stellen uns vor, dass der Jongleur leise mitzählt und bei jeder neuen Zahl ein neuer Wurf passiert.
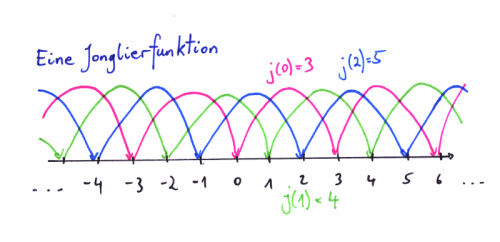
Die Würfe werden nun durch eine Funktion j beschrieben.
Dabei gibt j(t) den Zeitpunkt an, an dem der zur Zeit t geworfene Ball wieder gefangen werden soll.
Zum Beispiel: j(0)=3, j(1)=4, j(2)=5, j(3)=6,...
Das bedeutet: Der zum Zeitpunkt 0 geworfene Ball wird zum Zeitpunkt 3 wieder geworfen.
Zu den Zeitpunkten 1 und 2 finden zwei andere Würfe statt, die ebenfalls durch die Funktion j beschrieben werden.

Jedoch ist nicht jede Funktion j zum Jonglieren geeignet.
Wir müssen mindestens die folgenden Forderungen stellen.

1. Auf Deutsch: Ein Ball wird geworfen, zu einem späteren Zeitpunkt wieder gefangen.
   Auf Mathematisch: Es gilt j(t)>t für jeden Zeitpunkt t.
2. Auf Deutsch: Zu jedem Zeitpunkt muss ein Ball wurfbereit sein.
   Auf Mathematisch: Die Funktion j ist surjektiv, d.h., zu jedem t gibt es ein s mit j(s) = t.
3. Auf Deutsch: Zwei Bälle dürfen nicht gleichzeitig landen.
   Sie sind nämlich schwer zu fangen.
   Auf Mathematisch: Die Funktion j ist injektiv, d.h. wenn t und s unterschiedliche Zeitpunkte sind, dann sind auch die Zeitpunkte j(t) und j(s) unterschiedlich.

Eine Funktion, die die ganzen Zahlen auf sich abbildet und sowohl injektiv als auch surjektiv ist, nennt man Permutation.
Ein Mathematiker kann also diese Forderungen ganz kurz in folgender Definition zusammenfassen.

Eine Jonglierfunktion j ist eine Permutation der ganzen Zahlen mit der Bedingung j(t)>t für alle Zeitpunkte t.

In dieser Definition steckt nun die gesamte mathematische Beschreibung des Jonglierens.
Dabei wurden eine Reihe von Vereinfachungen gemacht.
In der realen Welt ist Jonglieren kompliziert: die Koordination der Hände, die Flugbahnen der Bälle, wie fängt man eigentlich an …
Aus der Sicht eines Mathematikers geht es nur darum, Jonglierfunktionen, also Funktionen, die obige Regeln erfüllen, zu untersuchen.

Ein erster oft hilfreicher Schritt zum besseren Verständnis ist eine gute Visualisierung.
Von jeder ganzen Zahl t zeichnet man einen Pfeil zum Funktionswert j(t).
Die unterschiedlichen Bälle werden durch unterschiedliche Farben markiert.
Das ist auch schon die erste mathematische Erkenntnis: Die Anzahl der benötigten Farben ergibt die Anzahl der jonglierten Bälle.
Später zeige ich noch, wie man die Anzahl der Bälle sogar ausrechnen kann.

Die folgenden Abbildung zeigt das einfachste Beispiel mit drei Bällen.

Nun hat man bereits zwei Möglichkeiten eine Jonglierfunktion mitzuteilen.
Man kann eine Formel wie j(t)=t+3 angeben oder man kann eine Zeichnung anfertigen.
Beides ist bei komplizierten Mustern unhandlich.
Gute Notation ist ein weiterer wichtiger Bestandteil von Mathematik.
Um Jongliermuster besser aufzuschreiben, kann man sich folgendes überlegen.

Für den Jongleur ist gar nicht die absolute Angabe der Wurfzeitpunkte interessant („der Ball zur Zeit 5 soll zur Zeit 10 wieder landen“) sondern er benötigt eine relative Angabe („dieser Ball soll 5 Würfe später wieder landen“).
Wir fassen dazu die Differenzen j(t)-t als Folge auf.
In dem vorhin diskutierten und gezeichneten Beispiel j(0)-0=3, j(1)-1=3, j(2)-2=3, j(3)-3=3,... oder kurz ...3333....
Wenn diese Folge periodisch ist, dann reicht es, eine Periode anzugeben.
Also ganz kurz 3.
Eine solche Angabe nennt man Jonglierfolge.

Die konstanten Jonglierfolgen 3, 4, 5, … sind dabei die jeweils einfachsten Muster, die man mit 3,4,5 … Bällen jonglieren kann.

Ich fasse kurz zusammen:

• Eine Jonglierfunktion ist eine mathematische Beschreibung des Jonglierens, die die Realität stark vereinfacht und die gewisse mathematische Regeln erfüllt.
• Zu jeder Jonglierfunktion j gehört eine Jonglierfolge.
  Sie wird durch die Formel j(t)-t gebildet.
• Bei periodischen Jongliermustern ergibt sich der große Vorteil, dass die Jonglierfolge eine ganz kompakte und praktische Notation ist.

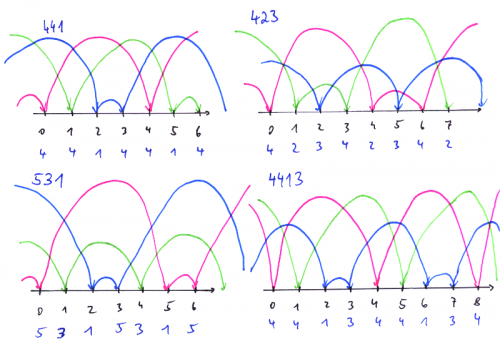
Im nächsten Bild werden die im Video vorgeführten Jonglierfolgen dargestellt.
Mit einem Klick auf die Jonglierfolge, kann man nochmal zur passenden Stelle im Video springen:
3,
441,
423,
531,
4413.

Die Bögen in den Zeichnungen haben keinen Bezug zur tatsächlichen Flugbahn der Bälle.
Da aber ein Ball, der länger fliegt, auch höher geworfen wird, kann man diese Intuition durch unterschiedlich hohe Bögen unterstützen.

Die Frage nach der Nützlichkeit eines mathematischen Modells diskutiere ich im dritten Teil dieses Artikels.
Zunächst will ich mich im zweiten Teil mit Mathematik beschäftigen.
Welche mathematischen Rätsel verbergen sich hinter Jonglierfolgen?

Teil 2. Mathematiker stellen Fragen und beweisen Antworten

Es gibt Jonglierfolgen, zum Beispiel 3, 441, 531 usw.
Mit ein paar Beispielen gibt sich ein Mathematiker nicht zufrieden, sondern er möchte die Systematik dahinter verstehen.
Dazu stellt er typischerweise Fragen wie

1. Ist jede Folge von Zahlen ein Jonglierfolge?
2. Gibt es ein Rezept um Jonglierfolgen erzeugen?
3. Haben Jonglierfolgen interessante Eigenschaften?
4. Wie kann man Jonglierfolgen erkennen?
5. Wie viele Jonglierfolgen gibt es?

Ich werde diese Fragen nicht erschöpfend behandeln.
Da Mathematiker aber viel Zeit mit der Beantwortung solcher Fragen verbringen, möchte ich andeuten, wie sie vorgehen und was sie dabei an Antworten erhalten.

Ich beginne mit der ersten Frage: Ist jede Zahlenfolge eine Jonglierfolge?
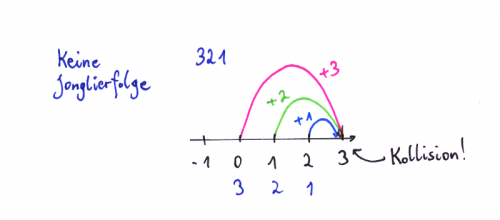
Betrachten wir zum Beispiel die Folge 321.
Wenn diese Folge eine Jonglierfolge wäre, dann gäbe es eine zugehörige Jonglierfunktion, die die Eigenschaften aus dem ersten Teil erfüllt.
Ich erinnere daran, wie diese Folge interpretiert wird:
Der zum Zeitpunkt 0 geworfene Ball landet zum Zeitpunkt j(0)=0+3=3, der zum Zeitpunkt 1 geworfene Ball landet auch zum Zeitpunkt j(1)=1+2=3 und der zum Zeitpunkt 2 geworfene Ball landet ebenfalls zum Zeitpunkt j(2)=2+1=3.
Alle drei Bälle landen also zur gleichen Zeit.
Das ist nicht zulässig!
Oder mathematisch ausgedrückt: Die zur Folge 321 gehörende Funktion j ist nicht injektiv, also keine Jonglierfunktion.

Um Jonglierfolgen eingehender zu untersuchen braucht man eine Idee.
Es hat sich herausgestellt, dass die folgende Konstruktion von großer Bedeutung ist.
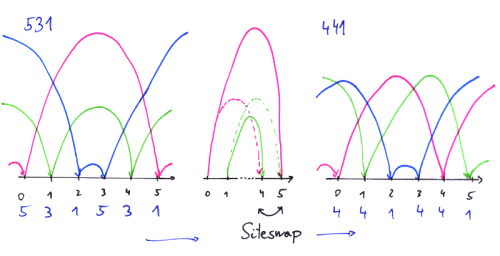
Betrachten wir ganz konkret die Jonglierfolge 531.
Es gilt j(0)=0+5=5 und j(1)=1+3=4.
Mit anderen Worten, der erste Ball landet zum Zeitpunkt 5, unmittelbar nach dem zweiten Ball, der zum Zeitpunkt 4 gefangen wird.
Die Schlüsselidee ist nun die: Wirft man den ersten Ball um 1 niedriger (j(0)=4 statt 5) und den zweiten um 1 höher (j(1)=4 statt 3), dann tauschen die beiden Bälle ihre Landezeitpunkte.
Damit wird die Folge 531 zur Folge 441 abgeändert.
Entscheidend ist, dass man die neue Folge jonglieren kann.
Dies wird durch den Tausch der Landezeitpunkte sichergestellt.
Jongleure nennen diese Operation Siteswap.

Im Allgemeinen erhält man folgende Formel zu Beschreibung von Siteswaps.
Es sei a1a2...am eine gegebene Jonglierfolge.
Der erste Ball bekommt den neuen Landezeitpunkt a2+1, der zweite Ball hingegen a1-1.
Die durch einen Siteswap erzeugte neue Jonglierfolge lautet dann (a2+1)(a1-1)a3...am.

Die Idee des Siteswaps sieht zunächst unscheinbar aus.
Tatsächlich aber handelt es sich in diesem Fall um eine ganz zentrale Einsicht.
Mit Hilfe von Siteswaps kann man nun einige weitere der anfangs gestellten Fragen beantworten.

Siteswaps ermöglichen es, jede Jonglierfolge in mehreren Schritten auf eine konstante Jonglierfolge zurückzuführen.
Ich führe das am Beispiel 531 vor.
Der erste Siteswap ergibt, wie eben gezeigt, 441.
Wendet man auf 441 nochmal einen Siteswap an, so kommt man zurück zu 531, das hilft nicht weiter.
Da die Jonglierfolge periodisch ist, erhält man das gleiche Jongliermuster, wenn man sie zyklisch im Kreis schiebt.
Bei 441 schiebt man die erste 4 ans Ende und erhält 414.
Ein Siteswap angewandt auf 414 ergibt 234.
Hier verschiebt man nochmals zyklisch die 23 hinter die 4 und erhält 423.
Ein letzter Siteswap ergibt 333, oder kurz 3.

Das allgemeine Resultat lautet

Jede Jonglierfolge kann durch Anwendung von Siteswaps und zyklischen Verschiebungen in eine konstante Jonglierfolge überführt werden.

Dieses Verfahren hat interessante Folgerungen.
Erstens kann man es auch umkehren.
Beginnt man mit einer konstanten Jonglierfolge, zum Beispiel 3, so erzeugt man mit Hilfe von Siteswaps alle anderen Jonglierfolgen mit drei Bällen.

Zweitens erkennt man bestimmte Eigenschaften von Jonglierfolgen.
Bei einer konstanten Folge ist der Mittelwert gleich der Anzahl der jonglierten Bälle.
Bei einem Siteswap ändert sich weder der Mittelwert der Jonglierfolge noch die Anzahl der benötigten Bälle.
Also ist die Anzahl der Bälle immer durch den Mittelwert gegeben.
Im Beispiel 531 ergibt sich (5+3+1)/3=3, man benötigt also 3 Bälle um 531 zu jonglieren.

In einer Jonglierfolge a1a2...am ist der Mittelwert (a1+a2+...+am)/m gleich der Anzahl der Bälle.
Insbesondere ist der Mittelwert eine ganze Zahl.

Somit kann man sofort ausschließen, dass z.B. die Folge 4423 eine Jonglierfolge ist.
Denn ihr Mittelwert ist (4+4+2+3)/4=3.25 und 3.25 ist keine ganze Zahl.

Ein ganzzahliger Mittelwert genügt aber noch nicht um Jonglierfolgen immer zu erkennen.
Zum Beispiel ist 321 keine Jonglierfolge, obwohl sie den ganzzahligen Mittelwert (3+2+1)/3=2 hat.
Eine genaue Analyse der Siteswaps zeigt, dass man wie folgt vorgehen kann.
Zu einer Folge a1a2...am bildet man die Hilfsfolge (a1+1)(a2+2)...(am+m) modulo m. Die Sprechweise „modulo m“ bedeutet, dass man den Rest bei Division durch m ausrechnet, also z.B. 7 modulo 3=1.
Es gilt der folgende

Permutationstest: Die Folge a1a2...am ist genau dann eine Jonglierfolge, wenn in der eben angegebenen Hilfsfolge jede Zahl von 0 bis m-1 genau einmal vorkommt.

Probieren wir das aus.
Zur Jonglierfolge 531 berechnen wir (5+1)(3+2)(1+3) = 654.
Schließlich ergibt 654 modulo 3 die Hilfsfolge 021.
Da in der Folge 021 die Zahlen von 0 bis 2 je genau einmal vorkommen, besagt also obiger Test, dass 531 eine Jonglierfolge ist.
Das ist richtig!
Betrachten wir als zweites Beispiel 321. Konstruktion der Hilfsfolge und Modulo-Rechnung ergibt 111.
In der Folge 111 kommt z.B. die Zahl 2 nicht vor.
Demzufolge ist 321 keine Jonglierfolge.
Auch das ist richtig!

Teil 3. Mathematiker interessieren sich nicht für die Realität — außer sie ist interessant

Im zweiten Teil haben wir uns ausschließlich mit Mathematik beschäftigt.
Es ging gar nicht mehr ums Jonglieren, sondern ich habe gezeigt, wie man bestimmte Zahlenfolgen, die gewissen Regeln gehorchen, besser verstehen kann.
Nun geht es abschließend um die Frage, ob aus diesem Vorgehen etwas Nützliches entstanden ist.

Tatsächlich hat das hier vorgestellte mathematische Modell praktische Bedeutung für Jongleure.
Der erste Nutzen ist, wie im ersten Teil aufgezeigt, die Möglichkeit einer effizienten Kommunikation von Jongliermustern.
Es gab Fachzeitschriften für Jongleure schon bevor Jonglierfolgen erfunden worden waren.
In ihnen wurden jedoch selten Jongliertricks erklärt.
Der Grund war die fehlende Möglichkeit einen Jongliertrick in kompakter Form schriftlich festzuhalten.
Heute sind Jonglierfolgen eine verbreitete Methode mit der sich Jongleure Tricks beibringen.

Ein zweites Ergebnis des mathematischen Formalismus ist die Systematik mit der Jongliermuster erforscht werden.
Vor der Erfindung von Jonglierfolgen waren viele Tricks und Muster bekannt.
Es fehlte aber die Übersicht.
Erst durch das mathematische Modell konnte man zum Beispiel systematisch sämtliche Möglichkeiten für das Jonglieren mit drei Bällen mit maximaler Wurfzeit 9 ausprobieren.
Einige der Muster waren schon lange bekannt.
Andere Muster stellten sich in der Praxis als neu, aber langweilig heraus.
Und ein paar Muster waren eine echte Bereicherung für das bis dahin übliche Jonglierrepertoire.
Die Mathematik war hier in der Lage Neues zu entdecken, das zuvor übersehen worden war.

Ein dritter Aspekt des mathematischen Zugangs zum Jonglieren ist die Abstraktion.
Zum Beispiel spielt in der Theorie der Jonglierfolgen die Anzahl der Hände keine Rolle.
Etwa kann ein Außerirdischer mit vier Händen Jonglierfolgen ebenfalls erfolgreich zum Jonglieren nutzen.
Ist das relevant?
Selbstverständlich!
Statt einem Außerirdischen kann man auch einen Freund hinzunehmen, dann hat man zusammen vier Hände zur Verfügung und es macht großen Spaß gemeinsam Jonglierfolgen auszuprobieren.

Ein vierter Punkt ist die Möglichkeit zur Verallgemeinerung.
Zu diesem Thema nur zwei Stichworte.
Es ist möglich zwei Bälle gleichzeitig aus einer Hand zu werfen, oder mit zwei Händen gleichzeitig zu werfen.
Diese beiden Vorgänge sind unter Jongleuren als Multiplex beziehungsweise Multihand bekannt.
Für beide Varianten gibt es entsprechende mathematische Beschreibungssprachen, die das im ersten Teil vorgestellte Modell erweitern.
Sofort ergeben sich neue mathematische Fragen: Kann man die Ergebnisse aus dem zweiten Teil auch auf diese Varianten übertragen?

Interessante mathematische Fragestellungen müssen sich nicht immer auf Anwendungen beziehen.
In den bisher betrachteten Jonglierfolgen kommen nur Zahlen kleiner gleich 9 vor.
Das entspricht in etwa den praktischen Möglichkeiten eines Jongleurs.
Nun kann man aber die Notation weiter treiben und A=10, B=11, usw. setzen.
Ein amüsantes Rätsel ist nun, Wörter zu finden, die gültige Jonglierfolgen beschreiben.
Zwei Beispiele: Mit 21 Bällen kann man die Folge THEOREM jonglieren, mit 23 Bällen sogar das Wort PROOF.
Der Leser ist an dieser Stelle eingeladen, diese Behauptung mit dem Permutationstest aus Teil 2 zu überprüfen und noch weitere jonglierbare Wörter zu finden.
Jonglieren mit 23 Bällen, das liegt außerhalb des Vermögens menschlicher Jongleure.
Grob geschätzt müsste man in der Jonglierfolge PROOF über 50 Meter hoch werfen.

Zum Abschluss noch zwei Literaturempfehlungen.

• Ein Buch übers Jonglieren: Charlie Dancey’s Encyclopaedia of Ball Juggling von Charlie Dancey. Butterfingers, 1994.
• Ein Buch über die Mathematik des Jonglierens: The mathematics of juggling von Burkard Polster. Springer, 2003.

Epilog

Nach der Lektüre eines Wissenschaftsblogs darf man die Frage stellen, ob man etwas gelernt hat.
In diesem Fall ist die Antwort: Nein.
Wer vor dem Lesen weder Jonglieren noch Mathematik beherschte, kann es jetzt immer noch nicht.
Diese Situation ist vergleichbar mit einem Violinkonzert: Wer einem Geiger eine Stunde zugeschaut und zugehört hat, kann auch danach keine Sonate spielen.

Trotzdem hoffe ich dem Leser einen Eindruck von typischen Arbeits- und Denkweisen eines Mathematikers vermittelt zu haben.
Das Erschaffen abstrakter Welten mit ihren eigenen, präzisen Regeln, die Neugier darin Fragen zu stellen, die Grenzen der Vorstellung auszuloten, die Beharrlichkeit Antworten zu finden, sei es für die Anwendung oder aus reiner Freude am Verstehen, all das beschäftigt Mathematiker.
Beim Jonglieren, und bei allem anderen.

© 2016 Andreas Geyer-Schulz

Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2016. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier. Das sagt der Autor des Artikels,...