Am Dienstag, dem 4. Oktober werden die Gewinner des diesjährigen Physik-Nobelpreises bekannt gegeben. Die Spekulationen über die Preisträger im Vorfeld sind Tradition. Ebenso Tradition wie meine Forderung, doch endlich Michel Mayor und Didier Queloz für ihre 1995 gemachte Entdeckung des ersten extrasolaren Planeten mit dem Nobelpreis auszuzeichnen. Das habe ich schon 2011 gemacht; ich habe es 2014 wiederholt und auch dieses Jahr wieder getan. Das Nobel-Komitee war bis jetzt allerdings anderer Meinung als ich, aber früher oder später müssen die beiden Schweizer den Nobelpreis kriegen!
Ob das 2016 der Fall sein wird, ist allerdings fraglich. Bei den üblichen Spekulationen tauchen sie jedenfalls nicht auf. Der Nachrichtenkonzern Thomson-Reuters hat wie jedes Jahr potentielle Kandidaten prognostiziert (basierend auf einer Auswertung der wissenschaftlichen Fachliteratur und der Anzahl der zitierten Forschungsartikel). Dass unter den drei Tipps von Thomson-Reuters die Gravitationswellen zu finden sind, ist keine Überraschung.
Der erste direkte Nachweis dieses Phänomens der im September 2015 gelungen ist, ist definitiv genau die Art von Forschung, die mit einem Nobelpreis ausgezeichnet werden muss und auch ausgezeichnet werden wird. Wenn nicht in diesem Jahr, dann auf jeden Fall 2017. Verglichen mit anderen Ergebnissen aus Großforschungsanlangen ist hier sogar halbwegs klar, wer die Preise bekommen soll. Ronald Drever, Kip Thorne und Rainer Weiss haben die Idee gehabt, ein Laserinterferometer zum Nachweis der Gravitationswellen zu bauen und dieses Projekt über Jahrzehnte hinweg gegen jede Menge Widerstände hin zum tatsächlichen Erfolg getrieben (ich empfehle zu diesem Thema das Buch “Black Hole Blues” von Janna Levin, das ich hier ausführlich beschrieben habe).
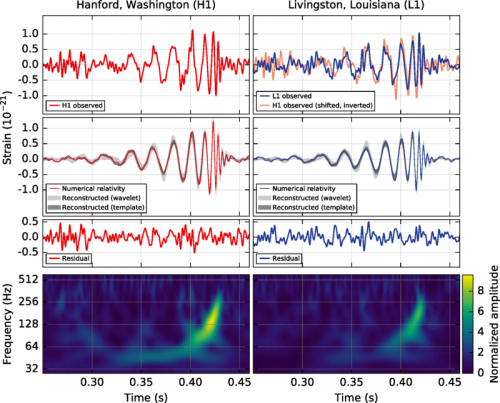
Genau so wie vorhergesagt: Die Erste direkte Beobachtung von Gravitationswellen mit dem LIGO-Interferometer (Bild: Abbott et al, 2016, CC-BY 3.0)
Natürlich ist es ungerecht, dass die vielen anderen Wissenschaftlerinnen und Wissenschaftler leer ausgehen, die am Bau des großen Gravitationswellenobservatoriums beteiligt waren; ebenso wie die Theoretiker und Numeriker ohne die der Nachweis nicht gelungen wäre. Aber so sind nun mal die Regeln bei der Nobelpreisvergabe… Einen kurzen Überblick über Gravitationswellen, ihren Nachweis und ihre Bedeutung für die Forschung habe ich hier veröffentlicht. Und viel mehr Informationen wird es natürlich überall geben, wenn für diese Entdeckung demnächst tatsächlich der Nobelpreis verliehen wird. Wenn es dieses Jahr nicht klappt, dann wohl nur aus bürokratischen Gründen – die Publikation der Ergebnisse erfolgte nach dem für die Vergabe relevanten Stichtag am 31. Januar – und nächstes Jahr ist es dann mit Sicherheit soweit.
Der zweite Nobelpreistipp von Thomson-Reuters lautet Marvin Cohen von der Universität Berkeley. Ich habe von ihm und seiner Arbeit noch nichts gehört, was aber auch nicht verwunderlich ist, da es sich um Festkörperphysik handelt. Die hat nicht nur wenig mit Astronomie zu tun sondern ist für Laien wie mich auch sehr schwer zu durchschauen. Schwer zu durchschauen sind auch die Forschungsobjekte von Cohen: Festkörper. Es ist ja schon ein wenig irritierend, dass wir zwar seit knapp 100 Jahren dank der Quantenmechanik eine wirklich wunderbare Theorie zur Beschreibung von Atomen und Elementarteilchen haben die ebenso wunderbare Ergebnisse liefert und kaum bessere Übereinstimmungen zwischen Vorhersage und Beobachtung zeigen könnten. Ein theoretisches Modell zur Beschreibung und Vorhersage der Eigenschaften von Festkörpern ist dagegen viel schwerer zu finden und das, obwohl diese Körper ja natürlich aus Atomen bestehen. Wie nutzt man also das Wissen um die einzelnen Atome um daraus vernünftige Vorhersagen über das Verhalten aus Atomen zusammengesetzter Festkörper zu treffen? Das war – wenn ich es richtig verstanden habe – das Forschungsgebiet mit dem sich Cohen beschäftigt hat.
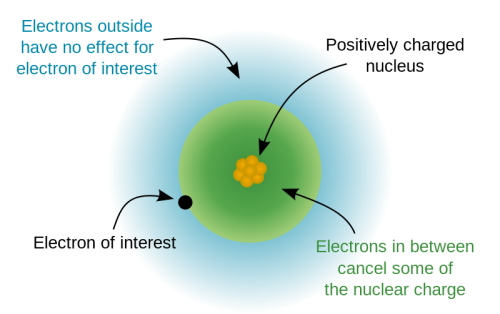
Und das, was schließlich den Durchbruch gebracht hat, war die von ihm mit entwickelte Methode der Pseudopotentiale: Ein Atom besteht ja immer aus einem Atomkern und Elektronen die die Hülle bilden. Es kann aber mehrere Hüllen geben, manche Elektronen befinden sich näher am Kern; manche weiter außen. Die äußerste Schicht der Elektronen wird Valenz-Elektronen genannt und sie sind es, die für die Interaktion mit anderen Atomen und deren Valenz-Elektronen zuständig sind. Die komplette Angelegenheit, also Atomkern, innere Elektronen und Valenz-Elektronen für jedes Atom zu beschreiben und dann auch noch die Wechselwirkung sehr vieler solcher Atome in einem Festkörper hat sich als sehr komplex herausgestellt. Zu komplex um wirklich praktikabel zu sein – weswegen die Methode der Pseudopotentiale sich darauf beschränkt die Valenz-Elektronen zu beschreiben und die inneren “Kern-Elektronen” einfach dem Atomkern zuschlägt (so zumindest habe ich das verstanden – falls jemand mitliest der mehr Ahnung von diesem Thema hat wäre ich dankbar für weitere Informationen bzw. Korrekturen). Das klingt relativ unspektakulär, aber wenn man erstmal so eine brauchbare Theorie zur Beschreibung von Festkörpern hat, dann kann man damit einiges anstellen. Man muss nur ein paar grundlegende chemische Eigenschaften (Masse, Zahl der Elektronen, …) der Atome kennen, die einen Festkörper ausmachen und kann dann dessen Verhalten vorhersagen. Man kann vorhersagen, welche Materialeigenschaften er haben wird. Zum Beispiel, ob und bei welcher Temperatur ein Material supraleitend wird! Oder mit diesen Modellen und Vorhersagen komplett neue Materialien entwickelt. Supraleiter, die bei hohen Temperaturen funktionieren vielleicht oder extrem dünne und leichte aber auch extreme reißfeste Materialien aus denen man einen Weltraumlift bauen könnte.
Etwas näher steht mir der dritte Nobelpreis-Tipp von Thomson Reuters: Es geht um die Kontrolle des Chaos. Das Chaos liegt mir sehr am Herzen; ich habe mich bei meiner wissenschaftlichen Arbeit intensiv mit der chaotischen Bewegung von Asteroiden und Planeten beschäftigt und meine Diplomarbeit sogar über ein ausschließlich chaostheoretisches Thema geschrieben. Ich war allerdings immer eher daran interessiert das Chaos zu beschreiben und zu verstehen, aber nicht es zu kontrollieren. Das ist aber die Leistung für die eventuell Celso Grebogi, Edward Ott und James Yorke mit dem Physik-Nobelpreis ausgezeichnet werden könnten.
“Chaos” ist ja viel mehr als nur die reine “Unordnung” die wir im Alltag mit diesem Begriff verbinden. In der Mathematik bzw. der Theorie der dynamischen System bedeutet “Chaos” etwas ganz anderes (und es war übrigens der eben erwähnte James Yorke der 1975 das Wort “Chaos” in die Mathematik eingeführt hat). Es geht dabei um ein zwar mathematisch beschreibbares Verhalten eines dynamischen Systems, das aber so sehr (und oft auch sehr überraschend) komplex ist, dass es quasi unmöglich ist, sein Verhalten konkret vorherzusagen. Wir können zum Beispiel sehr einfach beschreiben wie die Gravitationskraft zwischen den Planeten unseres Sonnensystems wirkt und wie sich durch diese Kraft ihre Bewegung verändert. Das ist kein Problem. Aber die Stärke der Wirkung hängt von der Bewegung ab und die Bewegung von der Stärke der Wirkung. Und da auch noch jeder Himmelskörper auf jeden anderen Himmelskörper einwirkt, ist das so entstehende System dank dieses Feedbacks so komplex, dass es keine simplen Regeln zur Vorhersage seines Verhalten gibts. Es ist chaotisch… Über die “seltsamen Attraktoren”, die “Fraktale”, die “Universalität” des Chaos und all die anderen faszinierenden Phänomene die auf diesem Gebiet auftreten können, habe ich ja schon früher berichtet. Allerdings noch nicht über die OGY-Methode, die sich eventuell bald als nobelpreiswürdig herausstellen könnte.
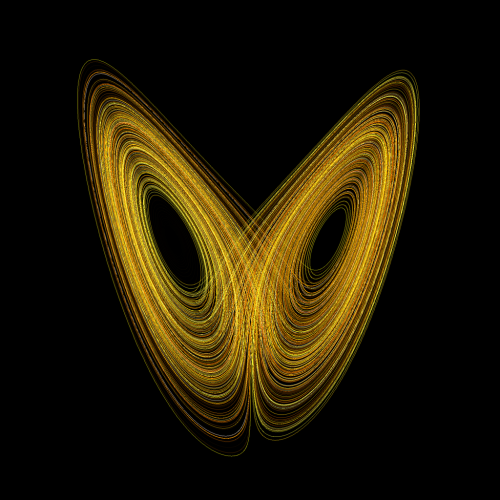
Ein seltsamer Attraktor (Bild: Public Domain)
“OGY” steht für die Nachnamen von Celso Grebogi, Edward Ott und James Yorke. Sie haben sich überlegt, wie man einen chaotischen Prozess so beeinflussen könnte um ihn weniger chaotisch zu gestalten. Chaos trifft man ja nicht nur in mathematisch-abstrakten Modellen sondern auch bei vielen realen Anwendungen. Bei chemischen Reaktionen zum Beispiel, die auch mal unvorhersagbar komplex ablaufen können. Überall dort wo Flüssigkeiten oder Gase strömen kommt es zu chaotischen Verwirbelungen und entsprechend unvorhersagbaren Phänomenen. Überall dort wo etwas schwingt, oszilliert oder sich sonst irgendwie einerseits periodisch bewegt und andererseits Rückkopplungen existieren, lauert das Chaos. Um es mit OGY zu kontrollieren, muss man es zuerst einmal untersuchen und verstehen. Man muss den sogenannten “Phasenraum” untersuchen, also sich vereinfacht gesagt alle möglichen Zustände ansehen, die das System einnehmen kann. Für bestimmte Ausgangssituationen werden das geordnete und regelmäßige Zustände sein; bei anderen Anfangsbedingungen chaotische und unregelmäßige Zustände, die man dann nach Möglichkeit vermeidet. Kritisch ist die Übergangszone: Wie ich schon in meinem Artikel über den seltsamen Attraktor beschrieben habe, ist genau sie es, die alles so kompliziert macht. Direkt neben einem Anfangszustand der zu völlig geordneten Bewegungen führt kann ein Zustand liegen der alles chaotisch macht. Schon winzigste Änderungen am Anfang reichen aus, um von der Ordnung ins Chaos zu wechseln. Chaotische und geordnete Bereiche sind so extrem in sich und ineinander verschachtelt, dass es unmöglich ist vorherzusagen, was passieren wird. Aber wenn man die Struktur so eines seltsamen Attraktors im Phasenraum gut genug kennt und weiß, in welchem chaotischen Zustand ein System sich gerade befindet, dann kann es mit einem kleinen “Schubs” in Richtung Ordnung befördern. Ein vereinfachtes Beispiel wäre zum Beispiel ein magnetisches Pendel, dass über ein paar Magneten hin und her schwingt. Sein Verhalten wird nicht regelmäßig sein wie bei einem normalen Pendel, das einfach und gleichmäßig hin und her schwingt. Die periodische Interaktion zwischen den Magnetpendel und den Magneten über das es schwingt sorgt für komplexe Störungen und das Pendel wird sehr komplex schwingen und seine Richtung und Schwingungsebene unvorhersagbar ändern. Wenn man nun aber die chaotische Struktur dieses Systems verstanden hat, kann man dem chaotischen Pendel in regelmäßigen Abständen einen kleinen (genau berechneten!) Schubs geben und so dafür sorgen, dass es vom chaotischen in einen regelmäßigen Zustand wechselt. Die hinter diesem simplen “Schubs” stehende mathematische Theorie ist natürlich enorm komplex (da geht es um so fiese Sachen wie hochdimensionale Mannigfaltigkeiten und ähnliches) – aber wenn es jeder könnte, dann gäbe es dafür ja auch keinen Nobelpreis!
Vielleicht gewinnt aber auch niemand aus dieser Vorhersage sondern jemand ganz anderes? Wie lauten eure Prognosen? Ich bin auch jeden Fall schon sehr gespannt!












Kommentare (12)