Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————
Gruss aus der Quantenwelt: Von einem fassbaren Modell für Unfassbares
von Kathi Keinstein
Ich bin Chemikerin sowie freischaffende Lehrerin und blogge über Natur und Wissenschaft für alle Sinne auf www.keinsteins-kiste.ch.
Gruss aus der Quantenwelt: Materieteilchen zeigen Interferenz! (Urheber: © TU Wien, mit freundlicher Genehmigung)
Quanten gelten für viele als eines der grössten Mysterien der Welt der Wissenschaft: Ob unscharf, getunnelt, verschränkt, teleportiert, als Teilchen, als Feld oder gar als Grundlage einer Heilmethode – über Quanten wird rege diskutiert…
+”*ç&ç%/(/(%ç**;:….
Dabei sind wir gar nicht so abgehoben oder gar magisch, wie viele behaupten, sondern bloss etwas ungewohnt für den menschlichen Denkapparat!
Hier sollte Kathi Keinsteins Beitrag zum Scienceblogs-Schreibwettbewerb stehen – die perfekte Gelegenheit, sich einzuklinken und mit ein paar intimen Einblicken in unsere Welt für Klarheit zu sorgen.
Was sind Quanten?
Wir sind Quanten. Nein, keine Füsse. Wir sind ausgewählte und voneinander abgegrenzte, also “diskrete” Portionen physikalischer Grössen. Mehr nicht. Aber für euch fangen wir gerne etwas ausführlicher von vorn an:
Die meisten Menschen haben die Erfahrung gemacht, dass eine physikalische Grösse jeden beliebigen Wert annehmen kann: Ein Auto kann (bis zum technisch möglichen Maximum) jede beliebige Geschwindigkeit (und damit jede beliebige Bewegungsenergie) haben. Und wenn es beschleunigt, durchläuft es all diese Geschwindigkeiten nahtlos hintereinander.
Vor etwas über 100 Jahren sind schlaue Köpfe jedoch darauf gestossen, dass das so nicht ganz stimmt. Die haben sich allerdings nicht mit Autos beschäftigt, sondern mit den wirklich kleinen Bausteinen der Welt. Und als sie diese Kleinteile mit physikalischen Grössen beschreiben wollten, fiel ihnen auf, dass diese Grössen nicht mehr jeden beliebigen Wert annehmen konnten, sondern nur ganzzahlige Vielfache winzigkleiner Mindestwerte. Und diese Mindestwerte sind wir – die Quanten.
Die Entdeckung der Quanten: Energie von Schwingungen
Die populärsten unter uns sind wohl die Lichtquanten, die ihr auch “Photonen” nennt, wie sie zum Beispiel von eurem Bildschirm abgestrahlt werden und in euren Augen chemische Reaktionen auslösen, die euch diesen Text sehen lassen. Lichtquanten sind minimal kleine Energie-Portionen, deren jeweilige Grösse von der Frequenz n des jeweiligen Lichtes abhängt:
Das h in der Gleichung ist übrigens das Wirkungsquant – eine Naturkonstante und quasi die Mutter aller Quanten. Denn diese wirklich total winzig kleine Zahl (rund 6,626*10^-31 Js) ist der Faktor, der unsere “Portionsgrösse” festlegt. Und wer ein wenig vom Rechnen versteht, ahnt nun schon, wie die ausfällt: Nämlich wirklich total winzig klein – für Frequenzen im irgendwie vorstellbaren Bereich.
Die Frequenz ist wiederum die Anzahl Schwingungen eines Systems pro Zeiteinheit. Wenn es um Quanten geht, kommt man um Schwingungen, also um periodisch wiederkehrende Abläufe, also nicht herum. So nahm Max Planck, der erste Mensch, dem wir in den Sinn kamen, an, dass unser Usprung in den Schwingungen der Bausteine der Materie läge. Diese Schwingungen, so Planck, könnten nur auf diskreten “Energie-Niveaus” ablaufen und damit nur diskrete Energieportionen von sich geben.
Damit hatte Planck im Grunde genommen auch recht: Die Energie-Niveaus gibt es wirklich. Ihr nennt sie “Orbitale” von Atomen (oder Molekülen) und sie können von “schwingenden” Elektronen besetzt werden. Dazwischen befinden sich verbotene Zonen, in denen sich kein Elektron aufhalten darf. Und trotzdem ist das Unmögliche möglich: Die Elektronen können über die verbotenen Zonen hinweg von einem Orbital ins andere “springen”. Eure Physiker nennen so etwas einen “Quantensprung” – und alle anderen Menschen verwenden dieses Wort gerne auch für alle anderen Arten sehr schneller, grosser Fortschritte.
In vereinfachter Form finden Energieniveaus und Quantensprünge bis heute in dem Schalen- oder “Hochhaus”-Modell Verwendung, mit dem Kathi Keinstein und die meisten Chemielehrer spannende Lichterscheinungen wie Farben, Fluoreszenz und Laserstrahlen erklären können.
Das Problem mit den Wellen
Erst ein weiterer kluger Kopf, nämlich Albert Einstein höchstpersönlich, ergänzte ein paar Jahre später, dass auch das Licht als solches portioniert sei, also aus Energie-Quanten bestehe. Das lässt sich leicht nachvollziehen, wenn man sich mit der Funktionsweise einer Solarzelle beschäftigt. Die beruht nämlich darauf, dass Licht in der Lage ist, einzelne Elektronen aus der Oberfläche von Halbleitern (oder Metallen) zu schleudern.
In Stockholm anerkannt: Auch Einstein hatte recht: Lichtquanten lösen Elektronen aus einer Oberfläche! (gemeinfrei)
Wie eine Billardkugel setzt ein Teilchen sich nämlich dann in Bewegung, wenn es von einem anderen Teilchen (bzw. einer anderen Billardkugel) angestossen wird. Demnach sollten Lichtportionen oder -“teilchen” die Rolle der weissen Kugel übernehmen und die Elektronen aus ihrer Bindung stossen können…
Oder doch nicht…? 1905, als Einstein mit seiner Idee von den Lichtquanten kam, war der Wissenschaft nämlich längst wohlbekannt, dass Licht aus elektromagnetischen Wellen besteht. Wellen sind periodisch wiederkehrende Erscheinungen, die sich ausbreiten – und von Schwingungen verursacht werden. In Experimenten kann man nachweisen, dass sich überschneidende Lichtwellen zu den gleichen Mustern führen wie einander kreuzende Wasserwellen: Es gibt Intereferenz!
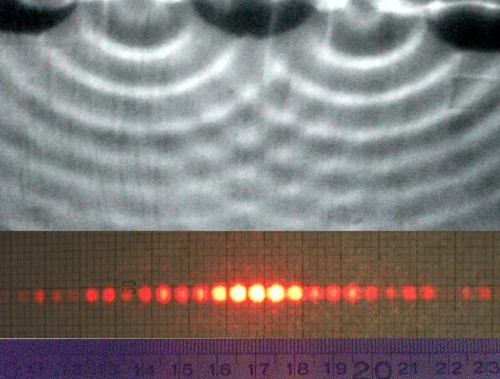
Oben: Interferenz zweier sich kreisförmig ausbreitender Wasserwellen nach Beugung an zwei Spalten. (gemeinfrei) Unten: Interferenz von Laser-Lichtwellen nach Beugung an einem Gitter aus mehreren Spalten. (Urheber: Shim’on and Slava Rybka [CC BY 3.0], via Wikimedia Commons)
Also was denn nun? Schlussendlich haben beide Behauptungen ihre Richtigkeit, auch wenn sie einander widersprechen: Teilchenströme erzeugen kein Interferenzmuster, Wellen stossen keine Teilchen an. Trotzdem kann Licht beides. Bis heute hat bloss noch kein Mensch ein anschauliches Modell gefunden, das alle Eigenschaften des Lichts unter einen Hut bringt. Deshalb sprecht ihr Menschen heute vom “dualistischen Modell”, wenn ihr sagt, dass Licht sowohl Eigenschaften von Wellen als auch von Teilchen hat.
Vom Licht zu Materiewellen
In der Mathematik ist die Sache etwas einfacher. Sowohl Wellen als auch Teilchen lassen sich mit mathematischen Gleichungen beschreiben, für welche überall und jederzeit die gleichen Regeln gelten. Zum Beispiel jene, die besagt, dass Ausdrücke in Gleichungen, welche in einer ihrer Seiten übereinstimmen, gleichgesetzt werden dürfen. Daran hielt sich auch Louis de Broglie, der zwei Gleichungen kannte: Jene für die Energie der Lichtquanten,
Und die berühmte Gleichung Einsteins, welche die Äquivalenz von Masse und Energie zum Ausdruck bringt,
In beiden steht auf der linken Seite “Energie”, was de Broglie dazu veranlasste, die beiden rechten Seiten gleich zu setzen und mit ein wenig Rechnen eine neue Gleichung zu erhalten, die aussagt: Jedes Teilchen – oder besser Objekt in Bewegung, das also mit Masse und Geschwindigkeit (also einem Impuls) aufwarten kann, hat auch eine Wellenlänge!
Demnach ist das dualistische Modell nicht nur für Licht zu gebrauchen, sondern ebenso für alle Arten von Materie. Und das haben Menschen im Experiment nachweisen können: Sie haben Interferenzmuster von Elektronen, Atomen und sogar recht grossen Molekülen wie dem Buckminsterfulleren oder gar Porphyrinen (Verwandten des Häm oder des Chlorophylls) mit bis zu 810 Atomen erzeugen können! Dass die Wellennatur von noch grösseren “Teilchen” wie Proteinen, Sandkörnern oder Tennisbällen nicht beobachtet werden kann, liegt einzig daran, dass deren Wellenlängen so kurz sind, dass bis heute (noch) kein Messgerät der Welt sie erfassen kann.
Und da man Gleichungen sowohl vor- als auch rückwärts lesen kann, zeigt sich, dass wo Wellen vorkommen, auch Quanten nicht weit sind: Elektronen sind die Quanten des Elektronenstrahls, der sich auch als Wellenbündel beschreiben lässt, Tennisbälle die Quanten des Bombardements aus der Ballmaschine…
Ihr seht: Im Grunde genommen sind wir Quanten gar nichts besonderes. In eurer alltäglichen Welt fallen wir bloss nicht auf, weil ihr unsere Wellen-Seite für eine zufriedenstellende Beschreibung eurer Beobachtungen nicht braucht. Sobald die Welleneigenschaften der Dinge aber messbar werden – und das ist bei sehr, sehr kleinen Dingen wie den “Elementarteilchen” der Fall – sieht die Sache ganz anders aus.
Von Materiewellen zur Quantenmechanik
So taugen Materiewellen nicht nur zur Beschreibung frei herumfliegender Teilchen, sondern auch von “gebundenen” Teilchen, zum Beispiel von Elektronen in Atomen, Molekülen oder anderen Verbindungen. Dazu geht man nicht von sich ausbreitenden, sondern von “stehenden”, in einem begrenzten Bereich “gefangenen” Wellen aus, wie man sie von einer schwingenden Geigensaite her kennt.
Nur Wellen im Kopf: Kathi Keinstein macht auch in ihrer Freizeit stehende Wellen. (Urheber: Die Elektronen-Quanten in der Selbstauslöser-Steuerung 😉 )
Die Mathematik dieser Materiewellen wird Quantenmechanik genannt. Analog zur klassischen Mechanik für das Verhalten alltäglicher, greifbarer Materieportionen beschreibt sie das Verhalten sehr kleiner Materieportionen (“Quantenteilchen”* eben). Die wohl populärste solche Mathematik ist die Schrödinger-Gleichung, die die Wellenfunktion einer stehenden Welle (z.B.) für ein Elektron im Atom beschreibt.
*dieser Pleonasmus, ein menschengemachtes Stilmittel, das auf der Zusammensetzung bedeutungsgleicher Wörter beruht, unterstreicht sehr schön, unter welchen Umständen wir für euch erst von Bedeutung sind: Wenn wir wirklich total winzig klein (und damit ebenso leicht) sind.
Warum wir Quanten den Menschen ungewohnt erscheinen
Ihr Menschen seid von Beobachtungen aus eurem Alltag gewohnt, dass die Dinge wie folgt ablaufen:
- Wenn man in eine Radarfalle fährt, zeigt das Foto nachher sehr genau, wo das Auto sich befand und welche Geschwindigkeit (und damit welchen Impuls) es hatte, gleich in welcher Reihenfolge diese Werte bestimmt werden. Auch wenn ihr das beim Anblick des Strafzettels noch so bedauert.
- Ein Objekt in einem festgelegten Zustand hat bestimmte Eigenschaften (“Zahlenwerte”): Wenn man Kugeln unter identischen Bedingungen abfeuert, landen sie alle am gleichen festgelegten Ort. Ein guter Schütze mit ruhiger Hand trifft deshalb bei gleichbleibenden Windverhältnissen wiederholt ins Schwarze.
- Wenn man die Bahn einer Kugel berechnet und sie nach dem Abfeuern beobachtet, findet man die Kugel verlässlich zu jeder Zeit am erwarteten Ort und nur da – einschliesslich des Treffers, den der Schütze anschliessend auf der Zielscheibe begutachten kann.
- Wenn man die Kugel durch eine Lichtschranke feuert und so ihre Flugbahn und Geschwindigkeit detektiert, ändert das am Treffer nichts.
Was die wirklich kleinen Quanten tun:
- Wenn man ein Quant mit einer “Radarfalle” erfasst, ist entweder das “Foto” unscharf oder die Geschwindigkeit wird ungenau erfasst. Beides zusammen lässt sich nicht genau festhalten!
- Wenn man einen Lichtstrahl auf einen “Schirm” richtet und die dort auftreffenden Lichtquanten einzeln detektiert, stellt man fest, dass unter gleichartigen Bedingungen abgestrahlte Quanten zufällig verteilt auftreffen – versucht man, den Strahl durch einen Spalt einzugrenzen, zeigt sich eine eingeschränkte, aber nach wie vor zufällige Verteilung!
- Verwendet man zwei Spalte statt einem, zeigt sich statt zwei Verteilungen ein Interferenzmuster! Das heisst, die Quanten bringen es irgendwie fertig, beide Spalte zugleich zu durchfliegen, was eine Interferenz erst möglich macht. Den befremdlichen Umstand, dass Quanten mehr als einen Zustand (hier ihre Position bzw. ihre Flugbahn) gleichzeitig einnehmen können, hat Erwin Schrödinger (genau, der mit der Gleichung) mit seiner berühmten Analogie mit der Katze in der Kiste greifbarer zu machen versucht.
- Wenn man zudem erfasst, durch welchen Spalt jedes Lichtquant fliegt, gibt es kein Interferenzmuster mehr: Die Messung verändert den Zustand der Quanten von “durch beide Spalten gleichzeitig” zu “durch einen bestimmten Spalt”!
Das alles war übrigens selbst einem schlauen Kopf wie Einstein nicht geheuer, zumal es mit seiner allgemeinen Relativitätstheorie nicht in Einklang gebracht werden konnte und kann.
Warum erscheint euch die Quantenwelt so anders?
Der Knackpunkt, der zu allen anderen Seltsamkeiten rund um uns Quanten führt, ist der Umstand, dass wir unseren Zustand ändern, sobald wir uns beobachtet fühlen (Punkt 4). Denn je nachdem, welche Eigenschaft ihr beobachtet (messt), ist diese Änderung eine andere. Das bedeutet, wenn ihr Beobachtungen verschiedener Eigenschaften anstellt, kann unser Endzustand – das Resultat der Verkettung der Beobachtungen – unterschiedlich ausfallen, je nachdem, welche Reihenfolge eure Messvorgänge haben!
Eine “Beobachtung” oder “Messung” ist übrigens nichts anderes als eine Wechselwirkung zwischen Objekten. Einfach gesagt: Wenn ihr etwas anschaut, sind Lichtquanten auf die elementaren Bestandteile dieses Etwas gefallen, haben sich mit diesen ausgetauscht und sich anschliessend weiter bis in euer Auge ausgebreitet, um dort erneut zu wechselwirken und so den Eindruck des Sehens zu erwecken. Technische Messgeräte funktionieren im Prinzip auch nicht anders.
Da somit jede eurer Beobachtungen eine ganze Menge von Wechselwirkungen zwischen winzigen Objekten mit sich bringt, könnt ihr deren Reihenfolge letztlich nicht kontrollieren. So “seht” ihr die vermeintlich gleichartig abgestrahlten Lichtquanten zwangsläufig wie zufällig auf dem Detektorschirm verteilt. Und das ist natürlich sehr unbefriedigend.
Wie sich Quantenphysiker in dieser befremdlichen Welt behelfen
Zum Glück haben kluge Köpfe auch da einen mathematischen Ausweg gefunden : Statt den Eigenschaften von sehr kleinen Objekten berechnet man die Wahrscheinlichkeit des Auftretens eben dieser Eigenschaften – denn das liefert “greifbare” Ergebnisse:
Max Born hat dazu für eine Materiewelle Psi als Funktion von Ort und Zeit festgelegt: Die Wahrscheinlichkeit, mit der sich das “Objekt” Psi zu einer bestimmten Zeit an einem bestimmten Ort aufhält, ist |Psi|^2 . Wo ihr uns also nicht direkt erfassen könnt, könnt ihr angeben, mit welcher Wahrscheinlichkeit ihr uns dort erfassen solltet. An verschiedenen Orten (bzw. in verschiedenen Zuständen) befinden wir uns also mit verschiedenen Wahrscheinlichkeiten.
Die Breite, über die sich solche Wahrscheinlichkeiten, die sich (massgeblich) von Null unterscheiden, verteilen, ist dabei eine genau nachvollziehbare Eigenschaft unsereines in der sonst so unscharfen Quantenwelt. So gibt zum Beispiel die Breite der Verteilung der Aufenthaltswahrscheinlichkeiten von Elektronen einem Atom seine Grösse – und den Orbitalen darin ihre “Gestalt”, die sich sogar in einem grafischen Modell darstellen lässt:
![Darstellung eines 1s-Orbitals eines Wasserstoff-Atoms: Je dichter die Punkte, desto wahrscheinlicher würde auf einer "Momentaufnahme" des Atoms dort ein Elektron zu finden sein! (Urheber: RJHall (Own work) [CC BY-SA 3.0], via Wikimedia Commons)](https://scienceblogs.de/astrodicticum-simplex/files/2017/09/Atomorbital_als_Punktwolke.jpg)
Darstellung eines 1s-Orbitals eines Wasserstoff-Atoms: Je dichter die Punkte, desto wahrscheinlicher würde auf einer “Momentaufnahme” des Atoms dort ein Elektron zu finden sein! (Urheber: RJHall (Own work) [CC BY-SA 3.0], via Wikimedia Commons)
Und was sind nun eigentlich Quantenfelder?
Bislang hat sich alle Quanten-Mathematik in diesem Artikel auf “abgegrenzte” Objekte, “Teilchen” bezogen. Ein “Feld” geht einen Schritt weiter: Dieses Stück Mathematik beschreibt die räumliche Verteilung einer solchen Grösse, beinhaltet also die Werte dieser Grösse (=”Feldstärke”) an allen Punkten eines Raumes. Ein Feld ist also zunächst einmal eine Zahlensammlung, ein mathematisches Werkzeug.
Manche Felder sind allerdings darüber hinaus richtige physikalische “Objekte”: Man kann ihre Bewegung mit sogenannten “Feldgleichungen” mathematisch beschreiben, wie z.B. für das elektrische und magnetische Feld mit den Maxwell-Gleichungen. Solche Felder haben zudem Eigenschaften wie Energie, Impuls bzw. Drehimpuls und können diese mit Körpern austauschen. So lässt sich Kraftwirkung zwischen Körpern im leeren Raum erklären: Ein Körper wechselwirkt mit einem Feld, und das Feld wechselwirkt wiederum mit einem anderen, vom ersten entfernten Körper.
Gemäss der Quantenfeldtheorie (eigentlich ist “eine Quantenfeldtheorie” eine Sammlung von Theorien, also mathematischem Werkzeug, für verschiedene Sorten Felder) sind – analog zur Quantenmechanik für Einzel-“Teilchen”- auch für die möglichen Verteilungen der Feldstärke diskrete “Stufen” vorgeschrieben. Die kleinstmöglichen diskreten Portionen von Feldstärken-Verteilungen werden dementsprechend “Feldquanten” genannt. Warum die Wissenschaftler nun von Quantenfeldtheorien und nicht von Feldquantentheorien sprechen, können wir euch allerdings nicht beantworten.
Nichts desto trotz sind Quantenfeldtheorien eine feine Sache. Aus ihnen können nämlich alle Eigenschaften der Materie und Kräfte entwickelt werden: Die Feldquanten entsprechen fundamentalen Elementarteilchen. Die werden in Materieteilchen und Austauschteilchen eingeteilt. Die wohl populärste und etablierteste solche Theorien-Sammlung ist wohl das “Standardmodell”, das alle Bestandteile der Materie und Kräfte umfasst – ausser der Gravitation. Die Suche nach einem Weg, die Gravitation und das, was die allgemeine Relativitätstheorie über sie sagt, nahtlos in die Sammlung des Standardmodells einzufügen und somit eine “grosse einheitliche Theorie” für den Aufbau der Welt zu schaffen, ist eine der spannenden Aufgaben eurer heutigen Physiker (deswegen verraten wir jetzt auch nicht, wie das geht – dann wäre ihnen ja fortan langweilig).
Wenn ihr nun aber mehr über Quantenfeldtheorien erfahren möchtet, findet ihr bei Martin Bäker von “Hier wohnen Drachen” eine sehr ausführliche Artikelserie darüber (–> ganz unten: “Quantenfeldtheorie für alle”).
Fazit
Quanten, ob als Grössen- oder Feldportionen, sind grundlegender Teil eines – zugegeben nicht ganz alltagsnahen – mathematischen Modells, also einer (ziemlich genauen, aber bis heute nicht ganz lupenreinen bzw. vollständigen) mathematischen Beschreibung der Natur der Welt.
Seiner dem Menschen ungewohnten Inhalte wegen, die es schwer verständlich machen, erscheint dieses Modell vielen “geheimnisvoll” bzw. “mystisch”, oder gar als willkommene Fundgrube für die Ausschmückung esoterischer “Weisheiten”. Aber es bleibt letztlich eines: Eine – zweifellos spannende – Sammlung mathematischer Werkzeuge. Und was eure Wissenschaftler damit bislang geschaffen haben und noch schaffen werden, ist eine wirklich aufregende Sache – auch ganz ohne Magie oder Esoterik.
Mit wahrscheinlich besten Grüssen aus dem Mikrokosmos,
Eure Quanten
Kommentare (71)