Sternengeschichten Folge 435: Der Kozai-Effekt

Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.

Mehr Informationen: [Podcast-Feed][iTunes][Bitlove][Facebook] [Twitter]

Über Bewertungen und Kommentare freue ich mich auf allen Kanälen.

—————————————————
Sternengeschichten Folge 435: Der Kozai-Effekt

Heute geht es in den Sternengeschichten um etwas, das man “Kozai-Effekt” nennt. Oder “Kozai-Mechanismus”. Oder “Kozai-Lidow-Effekt”. Oder “von Zeipel-Lidow-Kozai-Effekt”. Und alle anderen möglichen Kombinationen, je nachdem welchen von den Forschern die daran gearbeitet haben, man den Vorrang geben will. Bleiben wir bei dem japanischen Astronom Yoshihide Kozai und sagen “Kozai-Effekt”; das ist auch die übliche Bezeichnung. Die Namensgebung ist allerdings auch das einfachste an der Sache, es wird in dieser Folge ein wenig kompliziert. Aber nicht ZU kompliziert und zur Sicherheit fangen wir mal mit etwas ganz einfachem an. Nämlich mit einem Stern und ein paar Himmelskörper, die ihn umkreisen. Planeten, Asteroiden, und so weiter.

So etwas stellen wir uns ja gerne wie ein Uhrwerk vor. Die kleinen Himmelskörper sausen um ihren Stern herum, immer im Kreis und immer auf den gleichen Bahnen. Wenn wir das ganze dann irgendwo grafisch darstellen, machen wir das auch genau: Wir zeichnen einen Haufen Kreise um den Stern herum und verstärken dadurch noch den Eindruck, dass die Bahnen der Planeten und Asteroiden genau SO sind und auch so bleiben. Aber das ist falsch. Planetensysteme sind ein höchst dynamisches Phänomen. Da gibt es nichts, was sich nicht ändert. Das liegt, wie ich in den Sternengeschichten schon oft erzählt habe, an der Gravitationskraft. Jedes Objekt das eine Masse besitzt übt eine Gravitationskraft aus und zwar auf jedes andere Objekt mit einer Masse. Die Reichweite der Gravitationskraft ist theoretisch unbegrenzt, was genaugenommen heißt, dass ALLES im Universum von allem anderen beeinflusst wird. So kompliziert lassen wir es jetzt aber nicht werden, wir bleiben erstmal bei unserem Stern und ein paar Planeten und Asteroiden.

In erster Näherung stimmt das mit den unveränderlichen Bahnen schon. Die Erde zum Beispiel wankt ja jetzt nicht chaotisch durch das Sonnensystem. Sie zieht verlässlich ihre Runden um die Sonne, und braucht ebenso verlässlich 365,25 Tage um eine davon zu vollenden. Es gibt neben der Erde und der Sonne aber eben auch noch andere Himmelskörper im Sonnensystem. Die Gravitationskraft, die zum Beispiel der ferne Neptun auf die Erde ausübt, kann man aber erst mal vernachlässigen. Die ist wegen der enormen Distanz so gering, dass sie keinen relevanten Einfluss hat. Beim sehr viel näheren Mond sieht das aber schon anders aus. Beim weiter entfernten und sehr viel massereicheren Jupiter ebenso. Diese gravitativen Störungen der anderen Himmelskörper führen dazu, dass sich – auf ausreichend langen Zeiträumen betrachtet – die Bahn der Erde durchaus ändert. Sie wird ein bisschen größer und dann wieder ein bisschen kleiner. Sie ist mal kreisförmiger und mal ein wenig elliptischer. Sie wackelt ein bisschen hin und her. Die ganze Bahn dreht sich langsam um die Sonne herum. Würde man die Bahn der Erde tatsächlich als Strichspur im All sehen können und gäbe es einen “Fast Forward”-Knopf, mit dem man die Bewegung der Planeten beschleunigen könnte, dann würde man sehen, wie die Bahn wild pulsiert, sich dreht und windet. Allerdings nicht völlig chaotisch; es ist ein Pulsieren innerhalb gewisser Grenzen. Wäre es nicht so, dann hätte die Erde ja keine 4,5 Milliarden Jahre im Sonnensystem überlebt sondern wäre schon längst mit irgendeinem anderen Himmelskörper zusammengestoßen.

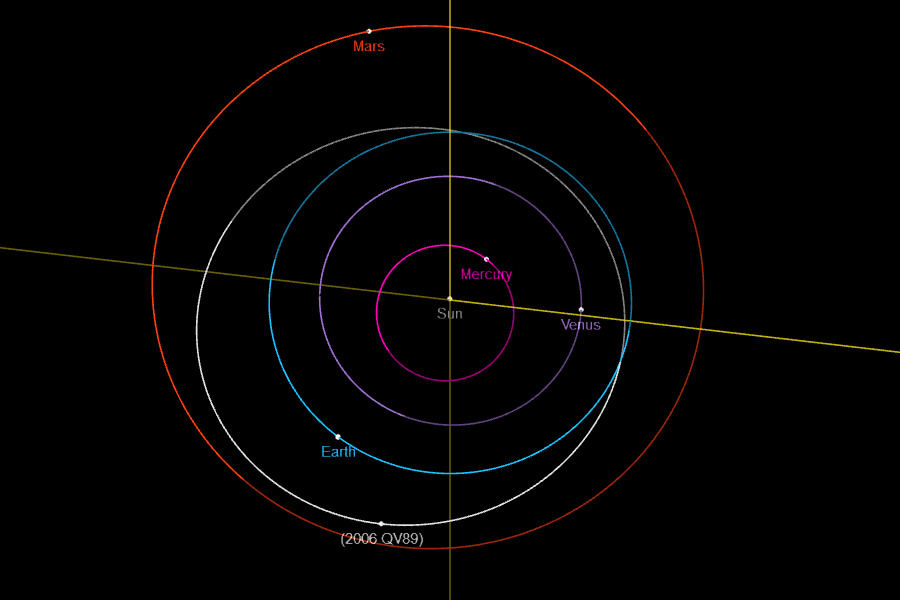
Umlaufbahnen sind keine Linien! (Bild: NASA/JPL)

Die Bahnen von Himmelskörper – von ALLEN Himmelskörpern – ändert sich also im Laufe der Zeit. Darüber gäbe es noch sehr viel mehr zu erzählen; das ist immerhin der komplette Forschungegenstand der Himmelsmechanik. Um den Kozai-Effekt zu verstehen, werden wir uns jetzt aber auf einen speziellen Fall beschränken. Wir schauen uns nur ein sogenanntes “Dreikörperproblem” an, also die Bewegung von drei Objekten. Und noch mehr: Es geht um hierarchische Dreikörpersysteme. Das heißt, einer der drei Körper ist weit entfernt von den beiden anderen. Wir können zum Beispiel einen Satelliten betrachten, der die Erde in ein paar hundert Kilometer Abstand umkreist. Und als dritten Körper nehmen wir den 400.000 Kilometer entfernten Mond. Oder einen Asteroid, der sich nahe an einem Stern befindet und einen Planeten, der weiter draußen seine Runden zieht. Oder einen Planeten, der von einem Mond umkreist wird und als dritten Körper den weit von beiden entfernten Stern. Wie auch immer – damit wir nicht komplett durcheinander kommen, werde ich ab jetzt die beiden Objekte die sich nahe sind, als das “innere System” bezeichnen. Der dritte, weit entfernte Himmelskörper ist der “Störer”. Und dann gehen wir noch davon aus, dass von den beiden Körpern des inneren Systems einer deutlich mehr Masse hat, als der andere. Was ja im Beispiel von Erde und Satellit oder Planet und Mond durchaus angenommen werden kann.

Jetzt können wir uns diesen Körper mit kleiner Masse genauer anschauen. Und damit meine ich keine astronomische Beobachtung mit dem Teleskop, sondern eine mathematische Analyse. Die Details lasse ich aus; in einem Podcast etwas vorrechnen ist immer ein wenig unattraktiv. Aber es gibt jede Menge Methoden, wie man die Bewegung dieses kleinen Körpers in Abhängigkeit der beiden anderen beschreiben kann. Wenn man das tut, dann kann man in diesem System auch eine Erhaltungsgröße finden. So etwas kennen wir ja auch aus anderen Systemen. Die Energieerhaltung zum Beispiel oder die Drehimpulserhaltung. Es kann aber auch diverse andere Erhaltungsgrößen geben, die nicht immer so anschaulich sein müssen. Das, um das es hier geht, nennt man ein “Integral der Bewegung”. Wenn sich Objekte auf eine bestimmte Art und Weise bewegen, dann gibt es eine Zahl, die sich errechnen lässt und die sich während der Bewegung nicht ändert. Ich weiß, das klingt alles enorm abstrakt. Weil es genaugenommen auch enorm abstrakt ist. Aber ich probiere es mal anders zu veranschaulichen. Wenn ich in gerade Linie von zuhause fort gehe, dann ändert sich die Distanz zu meinem Ausgangspunkt. Das ist nicht sonderlich außergewöhnlich und je weiter ich laufe, desto größer wird der Abstand. Er ist also definitiv nicht konstant. Wenn ich nun messe, wie weit ich noch laufen muss, bis ich auf meiner Umrundung der Erde wieder am Ausgangspunkt bin, dann wird auch dieser Abstand sich ständig ändern. Auch er ist nicht konstant. Aber die Summe der beiden Werte ist immer gleich, egal wie weit ich gelaufen bin. Die eine Zahl wird in dem Ausmaß größer, in dem die andere kleiner wird. Das hat nichts mit dem Kozai-Effekt zu tun und auch nicht einmal wirklich etwas mit einem echten Integral der Bewegung. Es liegt einfach nur daran, dass die Erde eine Kugel ist und ihre Größe immer gleich bleibt. Aber es soll ja auch nur demonstrieren, dass man unter bestimmten Umständen eine mathematische Größe finden kann, die sich im Laufe einer Bewegung nicht verändert.

Genau so eine Größe gibt es auch im Fall des vorhin beschriebenen hierarchischen Dreikörperproblems. Nimmt man die Exzentrizität der Bahn des kleineren Körpers des inneren Systems und multipliziert sie mit sich selbst, zieht das Ergebnis von 1 ab, berechnet die Wurzel aus dem Resultat und multipliziert das ganze dann noch mit dem Cosinus der Bahnneigung, dann kriegt man ein Integral der Bewegung. Oder nochmal anders: Die Wurzel aus 1 minus e² mal dem Cosinus von i ist immer konstant. Es gibt gute Gründe, warum das so ist und man kann das durchaus ohne allzu große Probleme berechnen. Wir schauen aber lieber auf das, was das eigentlich heißt. Es geht um die Exzentrizität e und die Bahnneigung i der Bahn des kleinen Körpers. Also des Satelliten, der die Erde umkreist oder des Mondes, der sich um einen Planeten bewegt. Die Exzentrizität gibt an, wie stark die Bahn von der Kreisform abweicht. Und die Bahnneigung, wie stark die Bahn gegenüber einer Referenzebene – in unserem Sonnensystem ist das die Erdbahn – geneigt ist. In der Formel des Integrals der Bewegung kommen nur diese beiden Werte vor. Und weil das Integral der Bewegung konstant sein muss, folgt daraus, dass sich beide Werte zusammen nicht unabhängig voneinander ändern können. Wird die Bahnneigung größer, dann muss die Exzentrizität kleiner werden und umgekehrt.

Yoshihide Kozai – lässt sich leichter visualisieren als seine Mathematik (Bild: Public domain)

Physikalisch liegt das daran, dass die Himmelskörper in so einer Konfiguration zwar Drehimpuls untereinander austauschen können, aber keine Energie. Das sind zwei klassische Erhaltungsgrößen, der Gesamtdrehimpuls aller drei Körper muss ebenso konstant bleiben wie die gesamte Energie im System. Wenn sie sich mit ihrer Gravitationskraft gegenseitig beeinflussen, dann können sie prinzipiell Energie und Drehimpuls austauschen. Die Energie äußerst sich dabei in der Größe der Umlaufbahn. Anders gesagt: Wird die Umlaufbahn eines Himmelskörpers größer, muss irgendwo anders eine Umlaufbahn kleiner werden, damit die Gesamtenergie erhalten bleibt. Für den Drehimpuls gilt das gleiche. Befinden sie sich drei Körper aber in der beschriebenen Konfiguration, dann findet kein Austausch von Energie statt. Die Umlaufbahnen bleiben alle gleich groß. Das einzige was sich ändern kann, ist der Drehimpuls und hier ist der Austausch an das Integral der Bewegung geknüpft. Es ermöglicht, vereinfacht gesagt, den Austausch von Exzentrizität in Bahnneigung. Ein bisschen so wie beim Geldwechseln: Exzentrizität und Bahnneigung sind zwei unterschiedliche Währungen und das Integral der Bewegung ist der Wechselkurs. Wenn ich also zum Beispiel einen Körper habe, mit kleiner Exzentrizität und großer Bahnneigung, also auf einer eher kreisförmigen Bahn, die stark geneigt ist, dann kann sie sich dank des Kozai-Effekts zu einer Bahn mit hoher Exzentrizität und kleiner Bahnneigung entwickeln. Das eine wird gegen das andere getauscht. Und umgekehrt geht es genau so.

Und jetzt wird das ganze schon ein bisschen weniger abstrakt. Stellen wir uns einen Kometen vor der sich in einer Kozai-Konfiguration befindet. Er hat eine einigermaßen kreisförmige Bahn, die dafür aber stark gegenüber der Erdbahn geneigt ist. Er wird nun von Jupiter gestört und die Bahn verändert sich. Wegen des Kozai-Effekts bleibt die Größe der Bahn der gleich. Am mittleren Abstand zwischen dem Komet und der Sonne ändert sich also nichts. Die Bahn wird aber deutlich elliptischer. Sie wird sehr viel langgestrecker als vorher und wenn die Größe dabei gleich bleiben muss, dann geht das nur, wenn der sonnennächste Punkt der Kometenbahn näher an die Sonne rückt als er vorher war. Ein Komet der dem Kozai-Effekt unterliegt wird also sehr viel näher als der Sonne vorbei fliegen als vorher und vielleicht sogar in sie hinein stürzen.

Damit dieses Wechselspiel von Exzentrizität und Bahnneigung stattfinden kann, braucht es eine bestimmte kritische Bahnneigung. Der Wert liegt bei circa 39 Grad: Unser Komet würde also erst dann anfangen, Bahnneigung gegen Exzentrizität einzutauschen, wenn seine Bahnneigung diesen Winkel überschreitet. Erst dann beginnen die für den Kozai-Effekt typischen Oszillationen von Exzentrizität und Bahnneigung. Die Exzentrizität steigt und steigt während die Bahnneigung sinkt. Wird die Bahn zu elliptisch, dann dreht sich das Spiel um. Sie wird wieder kreisförmiger, die Exzentrizität sinkt während die Bahnneigung steigt, bis der kritische Wert wieder überschritten ist und alles von vorne anfängt.

Dieser Mechanismus ist zwar etwas kompliziert, und es nicht unbedingt leicht zu sehen, warum es ihn geben muss. Aber er existiert und er spielt eine große Rolle bei der Bewegung von Himmelskörpern. Ein paar Monde des Jupiters und des Saturns etwa sind in genau so einer Konfiguration und zeigen Kozai-Oszillationen. Das kann unter Umständen auch schief gehen: Wird die Bahn eines Mondes zu exzentrisch, dann führt sie ihn immer näher an den Planeten heran. Dadurch werden die Gezeitenkräfte immer größer, bis der Mond davon auseinandergerissen und zerstört wird. Exzentrischen Bahnen sind prinzipiell gefährlich: Je langgestreckter die Bahn, desto größer die Chance, dass man einem anderen Himmelskörper in die Quere kommt und mit ihm kollidiert. Auch bei den Planeten anderer Sterne spielt der Kozai-Mechanismus eine Rolle. Dort haben wir immer wieder riesige Gasplaneten gefunden, die sich sehr nahe an ihrem Stern befinden. Diese “heißen Jupiter”, wie sie genannt werden, können dort aber nicht entstanden sein. Sie müssen von weiter außen im System nach innen gewandert sein und der Kozai-Mechanismus kann hier beteiligt gewesen sein. Er kann dafür gesorgt haben, dass die Bahn eines Planeten immer exzentrischer wurde und er so dem Stern immer näher kam. Durch die Gezeitenkräfte zwischen Stern und Planet wurde der Kozai-Mechanismus dann aber irgendwann ausgehebelt und die Bahn wieder kreisförmig. So ist der Planet dort gelandet, wo er sich jetzt befindet.

Heißer Jupiter dank Kozai-Effekt (Bild: NASA/CXC/M.Weiss))

Der Kozai-Mechanismus muss berücksichtigt werden wenn schwarze Löcher kollidieren, wenn sich Asteroiden durch ein Planetensystem bewegen oder wenn man Satelliten unter Kontrolle halten will. Er spielt immer dann eine Rolle, wenn sich Dinge bewegen und das ist überall im Universum. Er ist zugegebenermaßen nicht leicht zu verstehen wenn man die zugrundeliegende Mathematik nicht kennt. Aber es reicht fürs erste ja schon mal, wenn man weiß, dass es ihn gibt und für was er verantwortlich ist. Deswegen kommt jetzt noch mal alles in einem Satz: Der Kozai-Effekt beschreibt die periodische Veränderung der Bahn eines Himmelskörpers, bei der sich die Exzentrizität und Bahnneigung gegengleich verändern. Zum Klugscheißen auf der nächsten Party sollte das auf jeden Fall reichen.