Der Strand einer Insel ist voll mit Astronomie, wie ich gestern ausführlich erklärt habe. So schön so ein Strand aber auch ist, eines will man dort nicht haben: Große Schiffe! Die sollen nach Möglichkeit auf dem offenen Meer bleiben – wenn sie am Strand auflaufen ist im Allgemeinen irgendwas ziemlich katastrophal schief gelaufen. Das will man vermeiden und deswegen braucht man Leuchttürme. Man brauchte sie zumindest, als es noch keine moderne Satellitennavigation gab. Damals musste man schauen wohin man fährt und hoffen, etwaiges Land, das im Weg rumsteht, rechtzeitig zu entdecken. Und genau dafür waren Leuchttürme gut.

Der Leuchtturm von Norderney (a href=”https://de.wikipedia.org/wiki/Datei:Lt_norderney_2007_ArM.jpg”>Bild: Artmechanic, Gemeinfrei)
Ein Leuchtturm wie der “Große Norderneyer Leuchtturm”, der sich wenig überraschend auf der Nordseeinsel Norderney befindet und ebenso wenig überraschend, groß ist. Auf Norderney bin auch ich gerade (bzw. ab morgen; heute Abend bin ich noch in Hamburg und Gast in der “Neuen Deutschen Abendunterhaltung” bei Rocket Beans TV) und ich werde dem Leuchtturm sicherlich einen Besuch abstatten. Das Ding ist immerhin knapp 60 Meter hoch, höher als alles andere auf dieser Insel.
Und Höhe ist wichtig. Vor allem dann, wenn man weit schauen will (bzw. von weit weg gesehen werden möchte). Und es ist ziemlich überraschend, wie viel Einfluss die Höhe hat. Wir tun jetzt einfach mal so, als hätte nur allein die Höhe des Beobachtungsposten einen Einfluss auf die Sichtweite. In der Realität muss man natürlich das Wetter berücksichtigen, die Qualität der Atmosphäre, Nebel, Luftverschmutzung usw. Aber wenn man das ignoriert, dann kommt es nur darauf an, wie weit die Augen von der Erdoberfläche entfernt sind. Die Sichtweite kann man dann ganz leicht berechnen, dazu braucht es nicht mehr als den Satz des Pythagoras.
Wir zeichne einfach ein rechtwinkliges Dreieck. Eine Linie geht vom Erdmittelpunkt direkt durch unsere Füße bis zu unseren Augen. Von dort ziehen wir eine gerade Linie bis sie auf den Horizont trifft. Einen Horizont gibt es übrigens deswegen weil die Erde eine Kugel ist und wir nicht über die Erdkrümmung hinwegsehen können. Wie weit wir aber schauen können bevor sich die Erde vor unserem Blick nach unten krümmt, ist genau das was wir berechnen wollen. Dazu ziehen wir jetzt eine Linie die im rechten Winkel vom Horizont zurück zum Erdmittelpunkt führt. Wir haben jetzt also ein rechtwinkeliges Dreieck. Die Distanz vom Erdmittelpunkt bis zu unseren Augen ist die Hypothenuse und ihre Länge können wir leicht angeben: 6371 Kilometer plus ein bis zwei Meter, je nachdem wie groß man ist. Eine der beiden Katheten des Dreiecks ist einfach nur der Erdradius (die Linie vom Horizont zum Erdmittelpunkt). Bleibt die zweite Kathete, die ja nichts anderes ist als die Sichtweite und die berechnen wir einfach mit dem klassischen a²+b²=c².
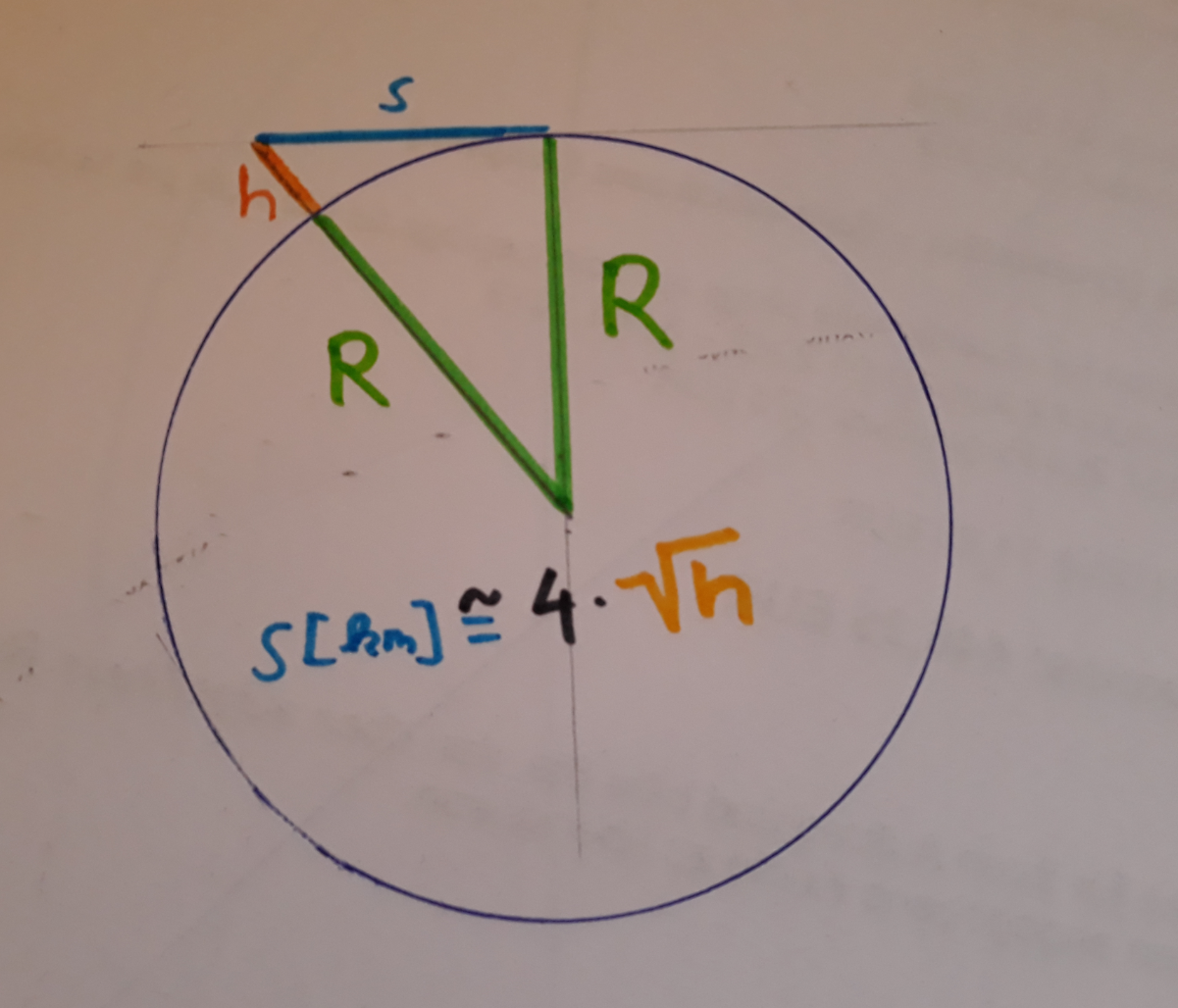
Skizze, nicht maßstabsgetreu (und ein wenig schmutzig, sorry)
In dem Fall können wir es uns noch ein wenig einfacher machen. Meine Augen liegen ja nur knapp 1,60 Meter über der Erdoberfläche, das fällt gegenüber den 6371 Kilometern des Erdradius nicht ins Gewicht. Vereinfacht man die Gleichung entsprechend (und berücksichtig man die Tatsache, dass die Atmosphäre das Licht bricht und man dadurch um ca 10 Prozent weiter schauen kann als rein geometrisch möglich), kommen wir zu dem Ergebnis, das die Sichtweite ungefähr gleich 4 mal die Wurzel aus der Augenhöhe ist (wer die Formel benutzen will muss darauf achten, die Augenhöhe in Meter einzugeben; das Ergebnis kommt dann in Kilometern raus). Ich kann also – klare Sicht und keine Hindernisse in der Sichtlinie vorausgesetzt – circa 5 Kilometer weit sehen.
Und es ist erstaunlich, wie sich die Werte ändern, wenn man die Augenhöhe vergrößert. Ich kann mir zwar auf die Schnelle keine längeren Beine wachsen lassen. Aber ich könnte mich auf eine 3 Meter hohe Leiter stellen. Und dann würde ich schon knapp 8.6 Kilometer weit sehen können: Fast 4 Kilometer weiter als zuvor. Und wenn ich auf den knapp 60 Meter hohen Leuchtturm in Norderney steigen würde, könnte ich fast 30 Kilometer weit sehen!
Das kann in der Praxis einen enormen Unterschied machen und das ist auch der Grund, warum Schiffe früher an ihren Masten ganz oben einen Ausguck hatten. Wer unten quasi auf Meereshöhe stand, sah nur ein paar Kilometer weit. 10 bis 20 Meter über dem Meer sah man aber bis 16 Kilometer weit und konnte entsprechend weit entfernte Schiffe ausmachen, die von Deck aus nicht zu sehen waren. Oder man konnte eben einen Leuchtturm schon sehen, wenn das Land noch ausreichend weit entfernt war, um den Kurs entsprechend zu korrigieren. Es sei denn, es war Nacht und das Leuchtfeuer kaputt…
P.S. Ja, das Lied von Knorkator kenn ich natürlich











Kommentare (13)