Ende August 2021 waren an der holländischen Wattenmeer-Küste in nur zehn Tagen über 190 tote Schweinswale (Phocoena phocoena) angespült worden. Das schreckte die für das Management der Schweinswalbestände zuständigen WissenschaftlerInnen und Behörden auf – normalerweise stranden dort im gesamten Jahr nur ungefähr 600 Kleinwale. Woher kam der plötzliche Anstieg? (s. auch Meertext: Nordsee: Woran sterben…
Unser Stammleser Gerald fragt sich (und uns), was man aus den Daten der Rosetta-Mission lernen konnte: “Hallo, anlässlich eines Bildes bei APOD Eine hohe Klippe auf dem Kometen Tschurjumow-Gerassimenko stelle ich mir die Frage, was eigentlich aus der Rosetta-Mission geworden ist. Zum Ende der Mission wurden beteiligte Wissenschaftler*innen zitiert, “man habe nun einige Jahre mit…
Der November 2021 wird in der Liste der tollsten Monate eher weit hinten landen. November an sich sind ja schon recht öde; Pandemie-November noch viel mehr und Lockdown-November sind die doofsten Monate die es gibt. Hier im Blog war zumindest ein bisschen was los. Nämlich das hier: Wissenschaft und Forschung Passend zum tristen November war…
Ein Mauersegler und eine sehr sexistische Alien-Pandemie: Die Buchempfehlungen vom November 2021
So. Wir haben November. In Österreich ist mittlerweile Lockdown Nummer 4 an der Reihe (oder 5, wenn man in Ostösterreich wohnt, so wie ich oder 3, wenn man in Theatern arbeitet, so wie ich und die Bühnen zwischen Nr. 2 und Nr 3. gar nicht erst aufgesperrt haben). Und in Deutschland wird es auch bald…
Zusammenfassung des Artikels: Teil 1: Die Impfung wirkt. Alle Impfstoffe. Zu 90 % gegen die meisten Virusvarianten, zu 75% gegen Delta. Sie ist die schärfste Waffe im Kampf gegen die Pandemie. Alle Impfstoffe wirken. Sie müssen einmal, bzw. zweimal mit einem gewissen Abstand gespritzt werden. Selbst falls sie die Ansteckung nicht vollständig verhindern können, verringern…
Der Schweinswal (Phocoena phocoena) ist zum Tier des Jahres 2022 gekürt worden! Der nur bis 1,80 Meter kleine Wal in Nord- und Ostsee ist scheu, meist unauffällig und stark bedroht. Einst weit verbreitet auch in norddeutschen Gewässern, ist er heute eher selten geworden, gerade die beiden Ostsee-Bestände sind bedroht, in der Zentralen Ostsee steht er…
Symplektische Geometrie ist die geometrische Interpretation der klassischen Mechanik. Man kann sie auf beliebigen symplektischen Mannigfaltigkeiten betreiben, was zur symplektischen Topologie führt. Diese bekam ihre wichtigsten Impulse durch die Arbeit an der 1974 in ihrer Allgemeinheit formulierten Arnold-Vermutung: ein Symplektomorphismus, der die Zeit-1-Abbildung eines Hamiltonschen Flusses ist, soll mindestens soviele Fixpunkte haben, wie die Summe…
Seit Februar 2020 leben wir im bedrohlichen Schatten von SARS-CoV-2 (severe acute respiratory syndrome coronavirus type 2), einem neuen Coronavirus. Mit der Zulassung und Verteilung von Impfstoffen verlor das fiese Virus einen Teil seines Schreckens. Ein Ende der Pandemie ist leider immer noch nicht in Sicht – obwohl eine wirksame Impfung, wirksame Hygienemaßnahmen und weitere…
Schnabelwale tauchen extrem lange und tief, an der Wasseroberfläche verhalten sie sich möglichst unauffällig: Das Leben der mittelgroßen Zahnwale ist geprägt von ihrer Furcht vor Orcas. Äußerlich sehen sie wie zu groß geratene Delphine aus, ihr auffallendstes Merkmal ist die oft seltsame Bezahnung: Bei den meisten Arten tragen nur erwachsene Männchen zwei bis vier Zähne…
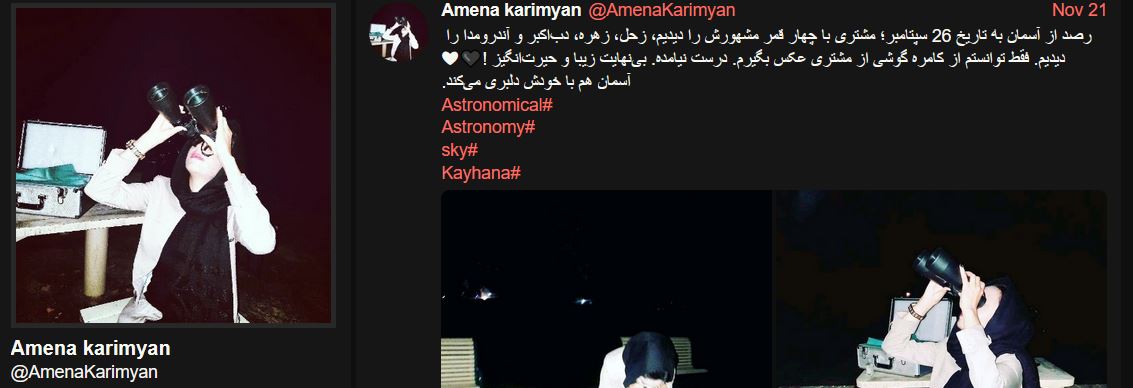
Die afghanische Astronomin und Aktivistin für Frauenrechte Amena Karimyan wurde von der österreichischen Akademie der Wissenschaften und der Universität Graz zu einem dreimonatigen Forschungsaufenthalt nach Österreich eingeladen. Die österreichische Botschaft in Islamabad (Pakistan) hat Karimyan ein Visum in Aussicht gestellt, das “nur” noch abgeholt werden muss. Amena Karimyan hat die für sie lebensgefährliche Reise von…