Wenn man lange genug bloggt (bei mir sind es inzwischen immerhin schon acht Jahre), kommt vermutlich zwangsläufig der Moment, an dem man sich mit einer Demonstration völliger Unkenntnis blamiert. Falls es bei mir nicht ohnehin schon so weit gewesen sein sollte, hole ich das heute mit einer möglicherweise ziemlich dämlichen Frage zu einer statistischen Formel nach, über die ich im Rahmen der Vorbereitung einiger Übungsaufgaben für meinen aktuellen Statistik-Kurs gestolpert bin.
Konkret geht es um die Formel zur Berechnung des sogenannten Quartilskoeffizienten der Schiefe – dem einzigen Maß für die Symmetrie (oder Asymmetrie) einer Verteilung, welches sich auch für ordinalskalierte Daten berechnen lässt (bei metrischen Daten greift man da ja eher auf den Momentenkoeffizienten der Schiefe zurück – zumindest solange, wie keine Ausreißer im Datensatz zu berücksichtigen sind). Um den Quartilskoeffizienten der Schiefe berechnen zu können, muss man lediglich die drei Quartilswerte (oberer Quartilswert p_0,75, Median / mittlerer Quartilswert p_0,50 und unterer Quartilswert p_0,25) berechnen, wie man sie unter anderem ja auch für die Konstruktion von Box-Plots oder die bekannte Fünf-Werte-Zusammenfassung benötigt. Die Formel zur Berechnung des Quartilskoeffizienten lautet:
Der sich ergebende Wert g_0,25 liegt stets zwischen +1 und -1, wobei Werte nahe 0 auf eine symmetrische, positive Werte dagegen auf eine linkssteile (und rechtsschiefe) und negative Werte auf eine rechtssteile (und linksschiefe) Verteilung hindeuten. Für eine ganz perfekt symmetrische Verteilung ist ein Ergebnis von 0 zu erwarten.
Sehen wir uns dies einmal an einem klassisch-ordinalskalierten Schulnoten-Beispiel mit 10 Schüler/innen an:
Note 1: 2 Schüler/innen
Note 2: 5 Schüler/innen
Note 3: 2 Schüler/innen
Note 4: 0 Schüler/innen
Note 5: 1 Schüler/in
Bringt man diese Werte in eine geordnete Reihenfolge, so ergibt sich folgendes Bild:
[1; 1; 2; 2; 2; 2; 2; 3; 3; 5]
Die Quartilswerte dieser Verteilung lassen sich leicht berechnen (eine ausführliche Erklärung spare ich mir an dieser Stelle, da ich ohnehin gerade an einem demnächst startenden Blog-Einführungskurs für die deskriptive Statistik sitze) und lauten:
x_0,75 = 3
x_0,50 = 2
x_0,25 = 2
Der Quartilskoeffizient der Schiefe berechnet sich somit wie folgt:
g_0,25 = [(3-2) – (2-2)] / [(3-2)] = 1/1 = 1 (d.h. linkssteil und rechtsschief)
Sehen wir uns nun einmal eine perfekt symmetrische Verteilung der Werte an:
Note 1: 1 Schüler/in
Note 2: 2 Schüler/innen
Note 3: 4 Schüler/innen
Note 4: 2 Schüler/innen
Note 5: 1 Schüler/in
Bringt man diese Werte in eine geordnete Reihenfolge, so ergibt sich folgendes Bild:
[1; 2; 2; 3; 3; 3; 3; 4; 4; 5]
Die Quartilswerte dieser Verteilung lauten:
x_0,75 = 4
x_0,50 = 3
x_0,25 = 2
Der Quartilskoeffizient der Schiefe berechnet sich somit wie folgt:
g_0,25 = [(4-3) – (3-2)] / [(4-2)] = 0/2= 0 (d.h. perfekt symmetrisch)
So weit, so gut. Nun sehen wir uns aber einmal diese Verteilung an:
Note 1: 0 Schüler/innen
Note 2: 1 Schüler/in
Note 3: 8 Schüler/innen
Note 4: 1 Schüler/in
Note 5: 0 Schüler/innen
Bringt man diese Werte in eine geordnete Reihenfolge, so ergibt sich folgendes Bild:
[2; 3; 3; 3; 3; 3; 3; 3; 3; 4]
Die Quartilswerte dieser Verteilung lauten:
x_0,75 = 3
x_0,50 = 3
x_0,25 = 3
Der Quartilskoeffizient der Schiefe berechnet sich somit wie folgt:
g_0,25 = [(3-3) – (3-3)] / [(3-3)] = 0/0= ???
Zu erwarten wäre auch hier ja ein Ergebnis von 0 (symmetrische Verteilung) – das Ergebnis einer Division durch 0 ist ja aber eben nicht 0, sondern vielmehr nicht definiert. Betrachtet man noch einmal die Formel
so ist festzustellen, dass das Problem einer Division durch 0 immer dann auftritt, wenn oberer und unterer Quartilswert identisch, der Interquartilsabstand (IQR, Inter Quartile Range) also 0 lautet. Da in solchen Fällen der Median ebenfalls identisch mit dem oberen und dem unteren Quartil sein muss, endet die Berechnung des Quartilskoeffizienten der Schiefe stets mit 0/0.
Nun zu meiner Frage: Bedeutet das nicht, dass sich der Quartilskoeffizient der Schiefe nur für Verteilungen berechnen lässt, die einen Interquartilsabstand größer 0 aufweisen oder dass der Quartilskoeffizient der Schiefe für alle Fälle, in denen der Interquartilsabstand der Verteilung bei 0 liegt, als g_0,25 = 0 definiert sein müsste? Und wenn dem so sein sollte – warum finde ich diese Einschränkung in keiner Formelsammlung und keinem Lehrbuch? Und wie erkläre ich den Studierenden verbal – also jenseits der Frage nach einer Division durch 0 – warum sich für bestimmte streuungsarme (die Verteilung im Beispiel ist ja nicht gänzlich streuungslos) Ordinal-Verteilungen keine Symmetrie/Asymmetrie bestimmen lässt?
Ich vermute mal, dass es auf diese Frage eine ganz einfache Antwort gibt – ich sehe sie nur gerade nicht. Vielleicht kann mit ja ein/e statistisch versierte/r Leser/in weiterhelfen…?

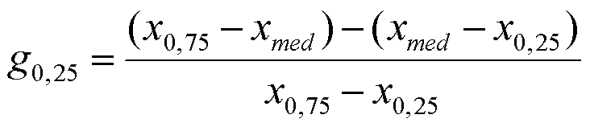
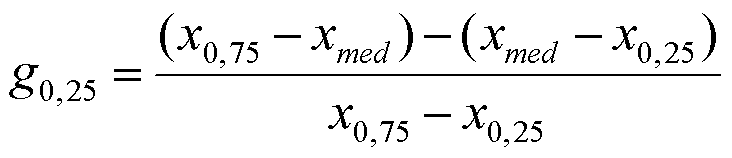

Kommentare (8)