Heute habe ich bei Twitter spaßeshalber eine Übungsaufgabe gepostet, die ich für eine meiner Statistik-Vorlesungen an der HS Harz vorbereitet hatte. Aufgrund der großen Anzahl an Kommentaren, Rückfragen und Bitten um das Posten eines Lösungswegs, stelle ich die Aufgabe samt Musterlösung hier im “Frischen Wind” ein, um eine URL zu bekommen, zu der ich verlinken kann. Vielleicht findet das Gedankenspiel hier ja noch weitere Freunde…
Erstelle #Statistik-Übungsaufgaben für die Studis. Wer sagt, dass es immer um Lotto, Würfel oder das Ziehen von Kugeln aus Urnen gehen muss? pic.twitter.com/ebDozC5WnF
— Christian Reinboth (@reinboth) May 30, 2017
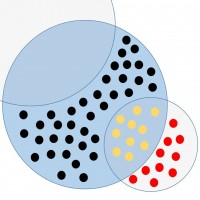
“Eine Behörde überwacht mit Hilfe einer Software die unverschlüsselte E-Mail-Kommunikation deutscher Internetnutzer*innen. Die Software, die E-Mails auf eine Reihe von Schlüsselbegriffen und Phrasen filtert, die auf illegale und / oder terroristische Aktivitäten hinweisen könnten, stuft eine tatsächlich sicherheitsrelevante Kommunikation mit einer sehr hohen Wahrscheinlichkeit von 99,5% als potentielle Bedrohung ein. Die Wahrscheinlichkeit dafür, dass eine harmlose E-Mail fälschlicherweise als potentielle Bedrohung klassifiziert wird, liegt dagegen nur bei 0,5%. In Deutschland gibt es 71.000.000 Internetnutzer*innen. Nachfolgend gehen wir davon aus,
- dass jeder Nutzer täglich 10 unverschlüsselte Mails verschickt, die von der Software gesichtet werden,
- dass 10.000 Nutzer das Internet für die Vorbereitung illegaler oder terroristischer Aktivitäten nutzen
- und dass jede vierte Mail, die von einem dieser 10.000 Nutzer verschickt wird, einen auffindbaren Hinweis auf eine solche Aktivität enthält.
Wie groß ist die Wahrscheinlichkeit dafür, dass eine an einem beliebigen Tag durch die Bedrohungen zu 99,5% korrekt klassifizierende Software als potentielle Bedrohung eingestufte E-Mail auch tatsächlich auf eine reale Bedrohungslage hinweist?”
Die korrekte Lösung dieser Aufgabe erfordert die Berechnung einer sogenannten bedingten Wahrscheinlichkeit – nämlich der Wahrscheinlichkeit dafür, dass es sich bei einer E-Mail tatsächlich um ein Indiz für ein kriminelles Vorhaben handelt – unter der Bedingung, dass die E-Mail zuvor bereits durch den Algorithmus als ein solches Indiz eingestuft wurde. Ohne an dieser Stelle die einschlägigen Formeln bemühen zu wollen (detaillierte Erläuterungen zum sogenannten Satz von Bayes finden sich in diesem Post aus meiner Statistik-Blogserie im Wissenschafts-Thurm), lässt sich die Aufgabe relativ einfach über die Betrachtung der absoluten Zahlen lösen. Dazu folgender Gedankengang:
1) Von 71.000.000 Internetnutzer*innen sind nur 10.000 kriminell – 70.990.000 von ihnen verschicken also vollkommen harmlose E-Mails. Macht bei 10 E-Mails pro Tag insgesamt 709.900.000 harmlose E-Mails.
2) Von den 10.000 kriminellen Nutzer*innen werden insgesamt 100.000 E-Mails verschickt – davon aber nur 25.000 mit belastendem Inhalt (jede vierte E-Mail). Macht weitere 75.000 harmlose E-Mails.
3) Die Software prüft somit insgesamt 710.000.000 E-Mails (10 pro Nutzer*in), von denen 25.000 kritisch und 709.975.000 harmlos sind.
4) Von den 709.975.000 harmlosen E-Mails wird die Software fälschlicherweise 0,5% = 3.549.875 E-Mails als verdächtig einstuften.
5) Von den 25.000 kritischen E-Mails wird die Software korrekterweise 99,5% = 24.875 E-Mails als verdächtig einstufen.
6) Insgesamt stuft die Software also 3.549.875 + 24.875 = 3.574.750 E-Mails als verdächtig ein, von denen aber nur 24.875 E-Mails wirklich verdächtig sind.
7) Dies führt uns zu einer Trefferquote von gerade mal 0,69%. Obwohl also die Software eine verdächtige E-Mail mit einer Wahrscheinlichkeit von 99,5% als verdächtig einstuft, sorgt die Masse der “false positives” – der fälschlicherweise ebenfalls als verdächtig eingestuften, eigentlich aber harmlosen E-Mails – für eine eher unbefriedigende Situation, in der die Wahrscheinlichkeit dafür, dass es sich bei einem konkreten Treffer tatsächlich um einen Kriminellen oder Terroristen handelt, deutlich unter 1% fällt.
Die Moral der Geschichte besteht natürlich darin, dass man sich – ganz besonders als politischer Entscheidungsträger – keinesfalls von der 99,5%igen Trefferquote blenden lassen darf, sondern sich vielmehr bewusst machen sollte, dass es bei jeder Form anlassloser Massenüberwachung allein aufgrund des extremen Missverhältnisses zwischen gesetzestreuen Bürgern und Straftätern unausweichlich ist, dass viele, viele Unbescholtene ins Visier von Behörden geraten. Selbst dann, wenn das System nahezu fehlerfrei (99,5%!) funktioniert.
Und ja: Natürlich hätte eine Software mit einer derart hohen Trefferquote einen Wert – nämlich dann, wenn sie im Rahmen der gezielten, richterlich angeordneten Überwachung von Einzelpersonen eingesetzt wird, die sich bereits aus anderen Gründen verdächtig gemacht haben – was – dies sei nur nebenbei bemerkt – bei sämtlichen Attentätern und Amokfahrern der letzten Jahre nahezu ausnahmslos der Fall war (“…war den Behörden bereits als Extremist bekannt…”). Überwacht man beispielsweise die elektronische Kommunikation von nur 10 Verdächtigen, von denen 9 wirklich Dreck am Stecken haben, steigt die Wahrscheinlichkeit für einen Treffer im Falle einer aussortierten E-Mail von 0,69% auf ganze 98,3% und erreicht damit schon fast die versprochenen 99,5%. Die Software ist also wirklich gut – sie eignet sich (wie auch jedes andere fehlerbehaftete System) schlicht nur nicht für die anlasslose Massenüberwachung… Übrigens gab es bei Twitter vorhin schon diese handschriftliche (!) Lösung:
@reinboth @anked pic.twitter.com/oGu0nsHKOz — Almut Helvogt (@AHelvogt) May 30, 2017
@reinboth @anked Der Unterschied beträgt nur 0,0001 Prozentpunkte. pic.twitter.com/E4Ihho9RA2 — Almut Helvogt (@AHelvogt) May 30, 2017
@reinboth @anked Stimmt! Also so? pic.twitter.com/6Y5RVK9qIs
— Almut Helvogt (@AHelvogt) May 30, 2017


Kommentare (71)