Da ich immer wieder auf der Suche nach neuen Ideen bin, mit denen ich meinen Einführungskurs in die Statistik noch etwas “aufpeppen” kann, belege ich derzeit den spannenden Coursera-MOOC “An Intuitive Introduction to Probability”, unterrichtet von Prof. Dr. Karl Schmedders von der Universität Zürich. Aus der Unterrichtseinheit zum Benfordschen Gesetz konnte ich schon mal einen Impuls mitnehmen – warum diese Gesetzmäßigkeit nicht im Unterricht anhand einer einfachen Excel-Tabelle sowie auf Basis von den Studierenden selbst ausgewählter Daten belegen, anstatt einfach nur davon zu erzählen und ein kurzes Beispiel zu rechnen? Wie man das in Excel schnell und einfach hinbekommt, habe ich nachfolgend zusammengefasst.
Was ist das Benfordsche Gesetz?
Das Benfordsche Gesetz (kein echtes Gesetz wie etwa die Newtonschen Gesetze) besagt (vereinfacht ausgedrückt), dass die Verteilung von Ziffern in empirischen Datensätzen (also solchen, die sich aus real erfassten Werten zusammensetzen) keine rein zufällige ist – so ist es beispielsweise sehr viel wahrscheinlicher, dass eine Zahl in einem solchen Datensatz mit der Ziffer 1 oder 2 anstatt mit der Ziffer 8 oder 9 beginnt. Dies ist für viele Menschen kontraintuitiv, da man eher erwarten würde, dass die Wahrscheinlichkeit für das Auftreten jeder Ziffer gleich hoch sein sollte. Tatsächlich sinkt die Wahrscheinlichkeit für das Auftreten von Ziffern mit der Höhe des Zahlenwertes aber immer weiter ab und verteilt sich wie folgt:
Wahrscheinlichkeit für Ziffer 1 an erster Stelle – 30,10%
Wahrscheinlichkeit für Ziffer 2 an erster Stelle – 17,60%
Wahrscheinlichkeit für Ziffer 3 an erster Stelle – 12,50%
Wahrscheinlichkeit für Ziffer 4 an erster Stelle – 9,70%
Wahrscheinlichkeit für Ziffer 5 an erster Stelle – 7,90%
Wahrscheinlichkeit für Ziffer 6 an erster Stelle – 6,70%
Wahrscheinlichkeit für Ziffer 7 an erster Stelle – 5,80%
Wahrscheinlichkeit für Ziffer 8 an erster Stelle – 5,10%
Wahrscheinlichkeit für Ziffer 9 an erster Stelle – 4,60%
Warum das so ist, wäre mal ein gutes Thema für einen ausführlichen Beitrag – und keinen schnellen Sonntagabend-Post. Wichtig zu wissen ist aber, dass man aus dieser Erkenntnis unter anderem Hinweise darauf ableiten kann, dass Datensätze manipuliert wurden – nämlich immer dann, wenn die Ziffernverteilung so gar nicht den Erwartungen folgt. Dies hilft nicht nur bei der Aufdeckung von Manipulationen am Finanzmarkt, sondern auch bei der Enttarnung von Wahlfälschungen oder auch verfälschten wissenschaftlichen Daten (kommt leider vor).
Und wie kann ich das nun selbst in Excel überprüfen?
Der spannende “Aha”-Effekt ist die Erkenntnis, dass sich die Anfangsziffern in zufällig ausgewählten (einige hundert Werte sollten es aber sein) Datensätzen tatsächlich nach dem oben aufgezeigten Schema verteilen – (fast) egal, an welchen Datensätzen man das testet. Um dieses Phänomen selbst in Excel erkunden zu können, braucht es lediglich drei Schritte:
Schritt 1: Geeigneten Datensatz finden
Eine gute Quelle für geeignete Datensätze ist die Webseite des Statistischen Bundesamtes – unter diesem Link findet man beispielsweise eine Excel-Tabelle mit den Bevölkerungszahlen und den Flächen (in km²) von 2061 deutschen Städten, mit der wir für unser Beispiel gut rechnen können. Aus dieser Tabelle habe ich nachfolgend drei Spalten (Name der Stadt, Flächengröße und Bevölkerungszahl) extrahiert.
Städtenamen, Flächengrößen und Bevölkerungszahlen in Excel.
Schritt 2: Ziffern an erster Stelle identifizieren
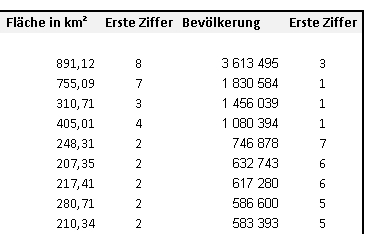
In beiden Datenspalten wollen wir nun die jeweils erste Ziffer der erfassten Zahlen betrachten. Diese kann man sich in Excel über die Funktion =LINKS(Zelle;Stelle) ausgeben lassen. Steht beispielsweise (wie hier) in Zelle C4 die Zahl 891,12, so erhalten wir die erste Ziffer dieser Zahl (8) über die Funktion =LINKS(C4;1). Vervielfältigt man diese Funktion nun in der Spalte neben der eigentlichen Datenspalte nach unten, so erhält man eine neue Spalte, in der sich jeweils die erste Ziffer jeder Zahl befindet.
Erweiterung der Tabelle um Spalten zur Ausgabe der ersten Ziffern.
Schritt 3: Ziffern an erster Stelle zählen
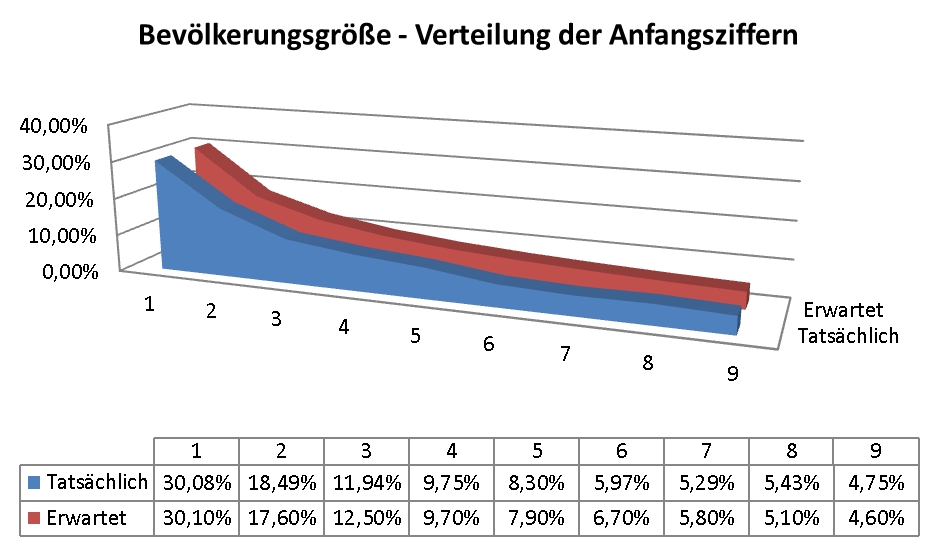
Im nächsten Schritt wollen wir diese Ziffern nun zählen, um festzustellen, wie oft die 1, die 2, die 3 usw. denn nun tatsächlich an erster Stelle der Zahlen im Datensatz aufgetreten sind. Hierzu verwenden wir die Funktion =ZÄHLENWENN(zu durchsuchender Zellenbereich; zu zählende Ziffer). Befinden sich unsere Ziffern an erster Stelle also in der Spalte D in den Zeilen D4 bis D2064, können wir uns die Anzahl an insgesamt aufgetretenen “3ern” über die Funktion =ZÄHLENWENN(D4:D2064;3) ausgeben lassen. Dies exerzieren wir für alle Ziffern durch und geben in einer weiteren Spalte dann noch die prozentuale Verteilung aus, um sie anschließend mit der zu erwartenden Verteilung vergleichen zu können.
Ergebnisse der Auszählungen und Abweichungen von der zu erwartenden Verteilung.
Et voilà. Wie man sieht, gelangt man in beiden Fällen zu dem Ergebnis, dass die Verteilung der Ziffern an erster Stelle verdammt dicht an der auf Basis des Benfordschen Gesetzes zu erwartenden Verteilung liegt. Faszinierend, oder? Probiert es am besten mal mit einem Datensatz eurer Wahl aus – bitte nur nicht vergessen: Der Datensatz sollte mindestens mehrere hundert – idealerweise aber mindestens mehrere tausend – Werte enthalten, die Ergebnis einer Messung oder Zählung, nicht aber einer Bewertung sind (d.h. Flächengrößen, Wassertiefen, Weglängen sind okay, Noten oder Präferenzrangfolgen sind es dagegen nicht).
Tatsächliche und zu erwartende Verteilung der Anfangsziffern bei der Bevölkerungsdichte.
Kommentare (5)