“Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experimentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radikale. Von Stund′ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.”
Dieses Zitat von Minkowksi, das in kaum einen Buch zur Relativitätstheorie fehlen darf, enthält eine der Kernaussagen der SRT: Raum und Zeit werden gemischt, man spricht besser von der Raum-Zeit.
Einstein selbst fand das Zitat anfänglich übrigens nicht so toll – später, in der Allgemeinen RT, vertrat er dann aber ähnliche (allerdings noch radikalere) Ansichten.
Bevor jemand Einspruch erhebt: Nein, die Relativitätstheorie ist nicht widerlegt, auch wenn wir da diese merkwürdigen Neutrinoexperimente haben. Selbst wenn sich zeigen sollte, dass die SRT “fehlerhaft” ist, so würden die bekannten Formeln (wie die Längenkontraktion oder die Zeitdilatation) weiterhin als Grenzfall gelten, dazu sind sie experimentell zu gut abgesichert.
Diese “Mischung” von Raum und Zeit zeigt sich zum Beispiel am Problem der Gleichzeitigkeit: Zwei Ereignisse, die für mich gleichzeitig sind, sind es zum Beispiel für Mark Brandis1, der mit hoher Geschwindigkeit in seiner Delta VII an mir vorbeibrettert, nicht unbedingt. Für mich trennt die beiden Ereignisse nur “Raum”, aber für den guten alten Mark scheint eins der beiden Ereignisse zeitlich vor dem anderen stattzufinden. Mein “Raum” ist für ihn eine Mischung aus “Raum” und “Zeit”. (Über Raumzeit habe ich ja schon mal einiges geschrieben.)
1Es muss ja nicht immer Perry Rhodan sein; und die Mark-Brandis-Bücher wurden vor kurzem ja neu aufgelegt – auch wenn die Höchstgeschwindigkeit der Delta VII natürlich weit unter der Lichtgeschwindigkeit liegt…
Eine praktische Methode, das zu veranschaulichen, sind Minkowski-Diagramme wie dieses hier (die habe ich neulich schon ausführlich erklärt, deswegen hier nur die – bei mir selbst geklaute – Kurzfassung):
Darin ist die senkrechte Achse die Zeit und die waagerechte Achse der Ort. Auf der vertikalen Achse steht dabei ct, also Lichtgeschwindigkeit mal Zeit – weil man mit Hilfe der Lichtgeschwindigkeit zwischen Zeiten und Strecken hin- und herrechnen kann. (Man rechnet also praktisch Zeiten in “Lichtmetern” (1Lm=1/300000000s).)
Das Tolle an Minkowski-Diagrammen ist, dass man ganz einfach ein Koordinatensystem für ein (mit konstanter Geschwindigkeit) bewegtes Objekt einzeichnen kann. Der Trick ist ganz einfach. Wen sich die Delta VII mit konstanter Geschwindigkeit bewegt, dann ist ihre Weltlinie eine schräg verlaufende also geneigte Gerade. Diese Gerade hat einen Winkel zu unserer senkrechten Achse. Sie entspricht deshalb der Zeitachse der Delta VII, deswegen beschrifte ich sie mit ct’:
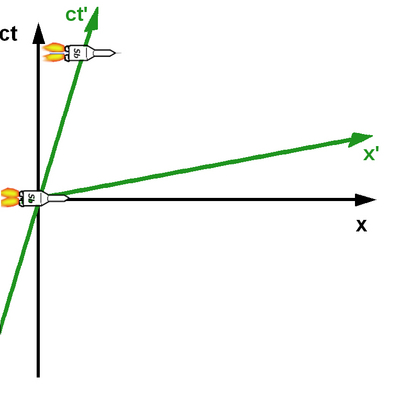
In das Diagramm habe ich auch die neue x’-Achse eingezeichnet – man bekommt sie aus der alten x-Achse, indem man sie um denselben Winkel rotiert – nur in entgegengesetzter Richtung.
Alle Punkte auf der grünen x’-Achse sind jetzt für Mark B. Ereignisse, die gleichzeitig stattfinden – während sie das für uns auf den Erdboden nicht tun. Dank des Minkowksi-Diagramms kann man leicht sehen, wie bestimmte Ereignisse in unterschiedlichen Bezugssystemen ablaufen.
Stellen wir uns beispielsweise vor, dass irgendwo rechts im Bild zu einem bestimmten Zeitpunkt eine Explosion stattfindet:
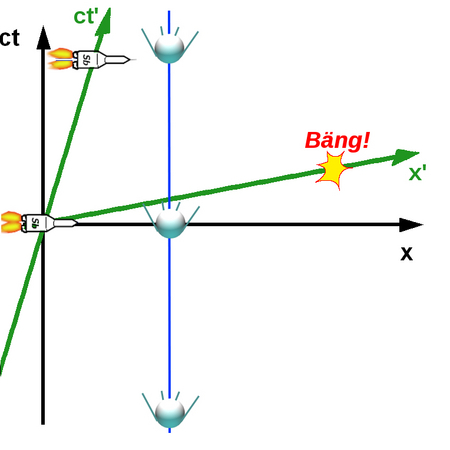
Von uns (da, wo der Satellit eingezeichnet ist) aus gesehen, passiert dies, nachdem das Raumschiff am Punkt Null (da, wo sich die schwarzen Linien kreuzen) durchgeflogen ist, aber vom Raumschiff aus gesehen sind beide Ereignisse genau gleichzeitig.
Raum und Zeit werden also miteinander vermischt, zwei Ereignisse, die aus Sicht von Mark B. nur “Raum” trennt, trennen aus unserer Sicht “Raum” und “Zeit”. Das bedeutet auch (und das ist der “Trick”, den wir in der QFT öfters verwenden werden): Wenn wir etwas über die Zeitabhängigkeit einer Größe wissen, dann können wir daraus gewisse Rückschlüsse darüber ziehen, wie sie vom Ort abhängt.






Kommentare (50)