Und das war ja genau der Grund, warum man der Schrödingergleichung, wie im ersten Teil erwähnt, sofort ansehen kann, dass sie nicht relativistisch ist, denn in ihr stecken Ort und Zeit in unterschiedlichen Ableitungen.
So wie Raum und Zeit vermischt werden, werden auch andere Größen vermischt. Nehmen wir beispielsweise die elektrische Ladung. Wenn ich neben mir einen gleichmäßig geladenen Draht liegen habe, dann hat dieser eine bestimmte Ladung, genauer gesagt, eine Ladungsdichte (also Ladung pro Volumen). Wenn der Draht ruht, ruhen auch die Ladungen im Draht.
Mark B. dagegen sieht die Sache ganz anders: Zum einen misst er zwar dieselbe Ladung, allerdings wegen der relativistischen Längenkontraktion auf einer kürzeren Drahtlänge – er sieht also eine höhere Ladungsdichte. Zusätzlich scheint es für ihn so, als würde der Draht an ihm vorbeisausen – er sieht also zusätzlich auch noch einen elektrischen Strom. Ladung und Strom (genauer gesagt: Stromdichte) werden also ebenfalls vermischt, genauso wie Zeit und Raum (und es gelten sogar dieselben Formeln). Es ist übrigens eine beliebte Aufgabe für Physik-Studis, zu zeigen, dass man das magnetische Feld eines Drahtes, in dem ein Strom fließt, auch über die Längenkontraktion der Ladungsdichte herleiten kann. Dieses Bild hier illustriert das Prinzip:
Wenn sich die Elektronen bewegen, dann sieht es vom Draht (mit ruhenden positiven Ladungen) aus so aus, als wären sie enger zusammengerückt – deswegen ziehen sich zwei stromführende Drähte an. Die Elektronen sehen umgekehrt die positiven Ladungen als enger zusammengerückt. Diese Anziehung zwischen zwei Drähten erklärt man normalerweise mit Hilfe des Magnetfeldes, aber man kann sie auch über die Lorentzkontraktion verstehen.
Müssten dann nicht auch das elektrische und das magnetische Feld irgendwie nach dieser Logik zusammenhängen? Ja, das tun sie auch. Allerdings nicht ganz direkt, sondern mit Hilfe der sogenannten Potentiale. Zu einem elektrischen Feld einer ruhenden Ladung gehört ein elektrisches Potential (das man aus dem Alltag als elektrische Spannung kennt). Bewegt sich die Ladung (oder bewegt man sich relativ zur Ladung – nicht umsonst heißt es ja “Relativitäts”-Theorie), dann kommt ein weiteres Potential hinzu, das Vektorpotential, das eng mit dem Magnetfeld zusammenhängt. (Die genaue Beziehung kann uns hier egal sein.)
(Zum Vektorpotential gibt es auch eine interessante Geschichte: In der klassischen Elektrodynamik wurde es als reine Rechengröße ohne jede “echte” Bedeutung eingeführt, aber in der Quantenmechanik zeigt sich, dass das Vektorpotential die Wellenfunktionen von Elektronen beeinflussen kann. Das ist der berühmte Aharonov-Bohm-Effekt. Als ich mal in Boston am Physik-Institut war, durfte ich übrigens im Büro von Aharonov sitzen – leider war er selbst nicht da.)
Elektrisches und Vektorpotential gehören also genauso zusammen wie Zeit und Raum oder Ladung und Strom.
Auch bei Wellen gibt es so eine Vermischung (und Wellen spielen in der QFT eine wichtige Rolle). Eine Welle wie diese hier
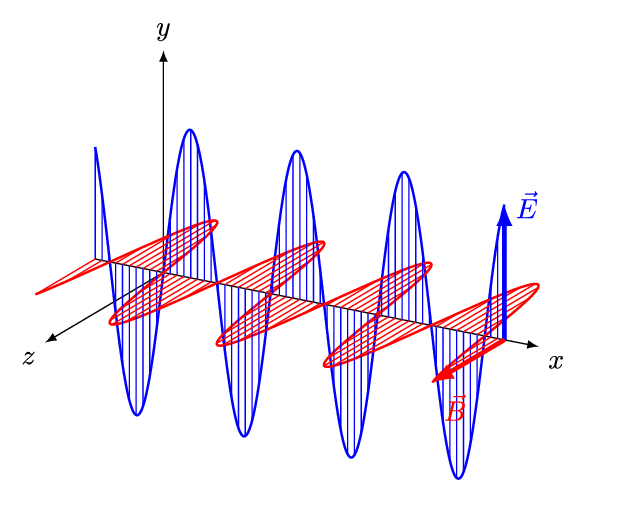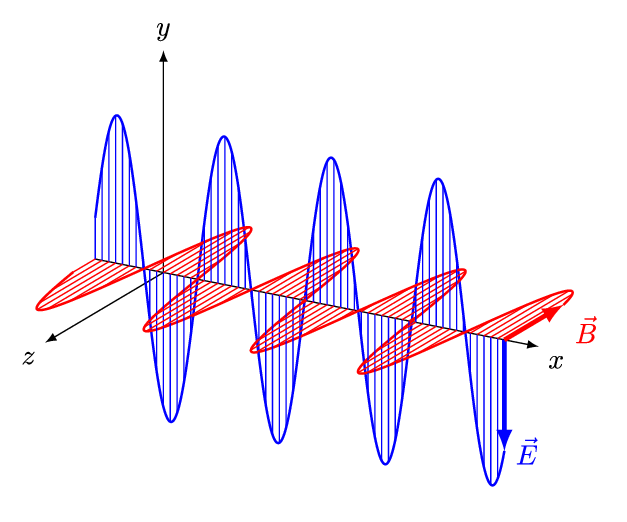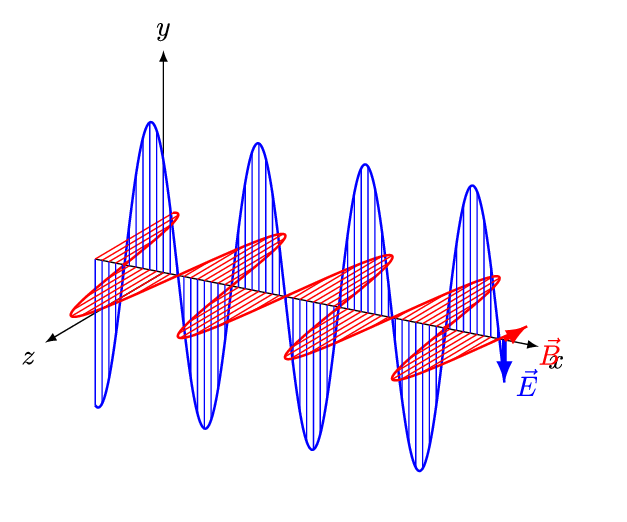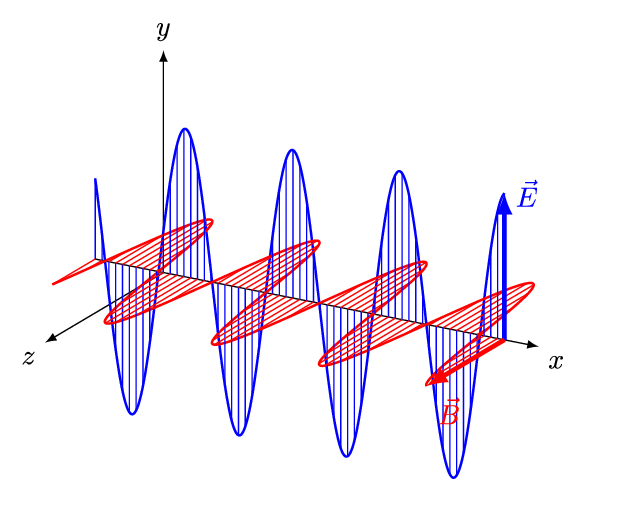
Von And1mu – Eigenes Werk, CC-BY-SA 4.0, Link
hat eine Wellenlänge und eine Frequenz. Zeichnet man die Wellenberge in ein Minkowski-Diagramm ein, dann sieht man, dass Mark B. an Bord seiner Delta VII wegen der Längenkontraktion und der Zeit-Dilatation eine andere Wellenlänge und eine andere Frequenz sieht, allerdings dieselbe Geschwindigkeit (wenn es sich um eine elektromagnetische Welle handelt, die sich mit Lichtgeschwindigkeit ausbreitet). Schreibt man statt der Wellenlänge den Kehrwert der Wellenlänge (die sogenannte Wellenzahl), dann gilt für Frequenz und Wellenzahl wieder derselbe Zusammenhang wie für Zeit und Ort.
Typischerweise baut man noch den einen oder anderen Faktor von 2π ein und verwendet die Kreisfrequenz ω = 2 π Frequenz und die Wellenzahl k=2 π / λ. Die Extra-π’s hier spart man sich dafür später anderswo wieder ein.
Noch ein fünftes Größenpaar gibt es, das in ähnlicher Weise vermischt wird wie Raum/Zeit, Ladung/Ladungsdichte, Potential/Vektorpotential, Frequenz/Wellenlänge. Dabei handelt es sich um Energie und Impuls.






Kommentare (50)