Das Higgs-Teilchen wurde zwar noch nicht endgültig gefunden, aber es ist zur Zeit in aller Munde. Das Higgs-Teilchen soll ja allen anderen (massiven) Teilchen die Masse verleihen. Aber warum ist das so? Wie soll das gehen – hängt es den Teilchen Gewichte um den Hals? Und warum können die Teilchen nicht einfach so eine Masse haben? Ist das nicht alles ziemlich weit hergeholt?
Hier will ich versuchen, euch den berühmten Higgs-Mechanismus zu erklären – eigentlich wäre das ein Teil meiner Quantenfeldtheorie-Serie, aber aus aktuellem Anlass erkläre ich es schon heute. Vorkenntnisse der Serie braucht ihr auch nicht, ich bleibe so einfach wie möglich. (Allerdings nicht so einfach wie manche anschauliche Erklärungen, die etwas von Gerüchten über Superstars auf Parties erzählen, das ist mir dann etwas zu vereinfacht.)
Das Standardmodell
Über das Standardmodell der Elementarteilchenphysik ist ja schon viel geschrieben worden – ich mache es hier kurz.
Es gibt zunächst zwei Sorten von “Materieteilchen” (die bezeichnet man oft als “Fermionen”), also solchen, aus denen sich die übliche Materie zusammensetzt. Da sind zum einen die Quarks, die sich zu Protonen und Neutronen zusammenschließen und damit die Atomkerne bilden, und dann die Leptonen: Dazu zählen Elektronen mit ihren schwereren Kumpeln, den Myonen und Tauonen, außerdem noch die berühmt-berüchtigten “Geisterteilchen”, die Neutrinos.
Dieses Bild zeigt das in einer Übersicht – aber keine Sorge, ihr müsste die ganzen Teilchen nicht auswendig kennen, um den Higgs-Mechanismus zu verstehen (Anmerkung: Nach einem update ist rechts das Higgs-Teilchen schon dabei):

Von MissMJ
derivative work: Polluks (talk) – Standard_Model_of_Elementary_Particles.svg, CC BY 3.0, Link
Diese Teilchen müssen natürlich auch etwas tun, sonst wäre die Welt ziemlich langweilig. Und da gibt es nicht so wahnsinnig viel, was Elementarteilchen tun können: Sie können von einem Ort zum anderen fliegen oder sie können andere Teilchen aussenden.1
1Ich schreibe hier alles in der Sprache der Feynman-Diagramme, also mit kleinen Bildchen, die zeigen, was die Teilchen so tun. Ganz korrekt wäre natürlich eine Beschreibung über Quantenfelder – aber wie gesagt, die Serie ist noch nicht so weit, dass ich den Zusammenhang zwischen Quantenfeldern und Feynmangraphen schon herstellen könnte.
Betrachten wir erstmal ein Teilchen (beispielsweise ein Elektron), das von einem Ort zum anderen fliegt, das können wir so darstellen:
Und dann kann ein Teilchen ein anderes aussenden, ein Elektron zum Beispiel ein Photon:
Hier kommt also ein Elektron an und sendet ein Photon aus. (Das Photon ist masselos.) Genauso gut kann das Elektron das Photon auch absorbieren (dazu würde man es von schräg rechts unten kommend zeichnen).
Photonen habe ich noch gar nicht erwähnt – die gehören nämlich nicht zu den “Materie-Teilchen” sondern sind “Bindungsteilchen” (auch gern “Bosonen” genannt). Bindungsteilchen werden gern durch Wellenlinien dargestellt (was an Lichtwellen erinnert, denn Photonen sind ja die Lichtteilchen). Im Bild oben sind das die rötlich eingefärbten Kästchen, an denen “Eichbosonen” dran steht.
An Bindungsteilchen gibt es das Photon und die Gluonen, die nur von Quarks ausgesandt werden können, aber mit den Leptonen nichts am Hut haben. Dann gibt es noch die so genannten “Vektorbosonen” W und Z – die werden gleich besonders wichtig werden. Ach ja, die Gravitation gibt es auch noch – zu der gehören als Teilchen die Gravitonen, aber da keiner genau versteht, wie die auf Elementarteilchenebene funktionieren, sind sie oben im Bild nicht mit drin.
Mit welcher Wahrscheinlichkeit ein Elektron ein Photon (oder ein anderes Teilchen) aussendet oder absorbiert (das ist mathematisch dasselbe), wird durch die sogenannte “Kopplungskonstante” beschrieben. Für Elektron und Photon ist das nichts als die elektrische Ladung des Elektrons (verziert mit ein paar Extra-Faktoren). Je größer die Kopplungskonstante, desto stärker wechselwirken die Teilchen miteinander (man sagt auch, desto stärker “koppeln” sie). Das wird später wichtig werden, wenn wir beim Higgs-Mechanismus ankommen.
Um Elementarteilchenprozesse zu berechnen, malt man jetzt kleine Bildchen wir zum Beispiel dieses hier:
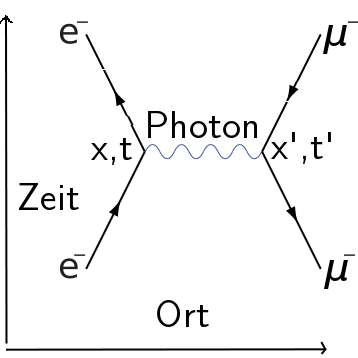
Ihr seht ein Elektron (e–) und ein Myon (μ–), die aufeinandertreffen und dabei ein Photon austauschen.1 Diese Bildchen sind nicht einfach bloß nette Veranschaulichungen (das sind sie auch, aber nicht nur), sondern sind verkappte Rechenvorschriften, sozusagen in einer Kurzschreibweise. Es gibt genaue Rechenregeln, nach denen ihr zum Beispiel ausrechnen könnt, wie groß die Wahrscheinlichkeit ist, dass dieser Prozess hier stattfindet, wenn die einfliegenden Teilchen bestimmte Eigenschaften haben. Ein netter Blogger hat das mal hier erklärt.
1Vielleicht wundert ihr euch, weil ich die Photonlinie ein bisschen schräg hätte zeichnen sollen. Tatsächlich ist es aber egal, ob das Elektron das Photon aussendet und das Myon es absorbiert oder umgekehrt – beide Prozesse müssen berücksichtigt werden, und man zeichnet es deswegen oft mit horizontaler Photonlinie. Der Link zum Thema Feynman-Diagramme erklärt das genauer.
Für uns hier wichtig ist vor allem die Rechenregel, die sagt, wie ein Teilchen von einem Ort zum anderen kommt, die also zu diesem einfachen Bildchen gehört:
Das zugehörige mathematische Objekt, das da berechnet wird, nennt man den Propagator – aber keine Angst, die Formel dafür brauchen wir nicht. Wichtig ist erst einmal nur, dass der Propagator von der Masse abhängt, und das ist eigentlich ja logisch: Ein ICE kommt anders von A nach B als eine Modelleisenbahn.
Das Problem der schwachen Wechselwirkung
Um zu verstehen, warum man einen Higgs-Mechanismus braucht, müssen wir uns die schwache Wechselwirkung (auch schwache Kernkraft genannt) näher ansehen: Das ist die, bei der die W- und Z-Teilchen eine Rolle spielen.
Diese Wechselwirkung kann nämlich Teilchen ineinander umwandeln. Beispielsweise kann aus einem Elektron ein Neutrino werden:
Das funktioniert als einzelner Prozess so nicht – sonst wären Elektronen instabil – aber es kann Bestandteil eines komplizierteren Prozesses sein, etwa so:
Hier wandelt sich ein Elektron in ein Neutrino um, das entstehende W-Teilchen verwandelt dann ein up- in ein down-Quark1.
1Auch hier könnte man die W-Boson-Linie horizontal zeichnen (sollte man eigentlich auch): Es ist egal, ob das Elektron ein W– aussendet oder ein W+ absorbiert, das kommt genau aufs selbe raus.
Ein wichtiges Beispiel für einen Prozess, der so ein W-Teilchen enthält, ist der Zerfall eines Neutrons in ein Proton, ein Elektron und ein (Anti-)Neutrino:

By Thymo – Own work by Thymo, Public Domain, Link
Dabei wandelt sich ein d-Quark des Neutrons in ein u-Quark um (Neutronen haben die Quark-Zusammensetzung udd, Protonen uud), sendet ein W-Boson aus, das dann zerfällt.
Bei der Analyse dieses Zerfalls entdeckte man etwas Erstaunliches: Der Prozess ist nicht spiegelsymmetrisch. Zwei Versuchsaufbauten, die sich nur darin unterscheiden, dass der eine ein exaktes Spiegelbild des anderen ist, zeigen unterschiedliche Ergebnisse. Das ist die berühmte Paritätsverletzung, für die es auch prompt einen Nobelpreis gab – die Geschichte dazu könnt ihr bei Jörg nachlesen.
Auch weitere experimentelle Ergebnisse zeigten, dass hier etwas Merkwürdiges passierte: Anscheinend hängen Prozesse, in denen W- oder Z-Teilchen eine Rolle spielen, von der Drehung der beteiligten Elementarteilchen ab.
Spin und Helizität
Gut, “Drehung” ist nicht ganz das richtige Wort – vornehm spricht man von Spin. (Im Englischen ist aber beides dasselbe Wort.) Den Spin von Elementarteilchen wirklich sauber zu erklären, ist alles andere als einfach. Stellt euch einfach vor, die Teilchen wären kleine Kugeln, die sich drehen, sie haben also eine Drehachse.
Nach den seltsamen Regeln der Quantenmechanik kann diese Drehachse – wenn man sie denn misst – nur in bestimmte Richtungen zeigen. Für die Teilchen, auf die es hier ankommt (das sind die Materieteilchen, also Leptonen und Quarks) zeigt die Drehachse immer entweder in die Bewegungsrichtung oder entgegengesetzt dazu. Man spricht auch von der Helizität. Teilchen können entweder rechtshändig rotieren oder linkshändig: Lasst den Daumen in die Bewegungsrichtung des Teilchens zeigen – die Finger geben dann die “Drehrichtung” des Teilchens an.
Die Untersuchung der schwachen Wechselwirkung zeigt jetzt, dass die Materie-Teilchen nur dann mit W- oder Z-Bosonen wechselwirken können, wenn sie linkshändig rotieren, aber nicht bei rechtshändigen Teilchen. Das war natürlich ziemlich ungewöhnlich und war einer der Gründe, warum es alles andere als einfach war, eine vernünftige Theorie dieser Wechselwirkung aufzustellen.
Mit etwas Trickserei gelang es tatsächlich, eine passende Theorie (die V-A-Kopplung (liest man “Vau-Minus-Ah”)) aufzustellen, deren Vorhersagen zum Experiment passten. Allerdings hatte diese Theorie einen massiven Schönheitsfehler.
Auf der Überholspur
Das Problem lässt sich in einem Satz formulieren: Wenn nur linkshändige Elektronen mit den W- und Z-Teilchen wechselwirken, was passiert dann, wenn ich ein Elektron überhole? Stellt euch das Elektron als kleine drehende Kugel vor, die durch die Gegend fliegt, sagen wir nach oben. Das Elektron soll linkshändig sein und kann dann an ein W oder Z koppeln. Jetzt fliege ich am Elektron vorbei, ebenfalls nach oben, und mit einer höheren Geschwindigkeit. Für mich sieht es so aus, als würde das Elektron nach unten fliegen. Damit wäre es rechtshändig und könnte nicht an die Ws und Zs koppeln. Dieses Bild macht das hoffentlich anschaulich:
Und das ist ja wohl Blödsinn – es kann ja kaum vom Beobachter abhängen, ob Elektronen nun ein Teilchen aussenden oder nicht; entweder das Elektron zerfällt, oder es zerfällt nicht, aber beides geht ja wohl nicht.
Damals nahm man noch an, dass Neutrinos masselose Teilchen sind. Für die gab es dieses Problem nicht, denn masselose Teilchen kann man nicht überholen, die fliegen immer mit Lichtgeschwindigkeit. Wenn Elektronen masselos wären, dann könnten wir unsere schöne Theorie retten.
Ja, klar. Und wenn Ideen Goldstücke wären, dann wären alle Physiker Millionäre. Masselose Elektronen? Gibt es da nicht so ein ganz paar Experimente, die zeigen, dass Elektronen eine Masse besitzen?
Aus Masse wird Wechselwirkung
In der Elementarteilchentheorie äußert sich die Masse eines Teilchens ja vor allem darin, wie es von A nach B kommt. Ihr erinnert euch vielleicht noch an dieses Bild von oben (hier vereinfacht ohne die Achsen):
Es zeigt, wie das Elektron von einem Ort zum anderen fliegt – den “Propagator”.
Und jetzt kommt ein ziemlich genialer mathematischer Trick: Man kann den Propagator für ein Teilchen mit Masse umschreiben in den für ein Teilchen ohne Masse. Das sieht dann so aus:
Links seht ihr den “normalen” Elektron-Propagator, rechts seht ihr eine Summe von Möglichkeiten, von A nach B zu kommen. Die gestrichelte Linie ist dabei der Propagator für ein “masseloses Elektron” (ihr nehmt also die Formel für den Propagator und setzt die Masse m einfach gleich Null). Das masselose Elektron fliegt aber nicht einfach von A nach B, sondern kann unterwegs “Zwischenstation” machen, einmal, zweimal oder mehrmal. (Und nach den Regeln für diese Art Rechnungen muss man alle diese Möglichkeiten addieren, um herauszubekommen, wie das Elektron nun genau von A nach B kommt.) Bei jeder Zwischenstation habe ich einen Kringel dran gemalt. Hier kann das Elektron seine Richtung und Geschwindigkeit wechseln, und mathematisch geht hier jetzt die Masse des Elektrons in die Berechnung dessen ein, was an diesem “Kringel” passiert. Zwischen den “Kringeln” fliegt das Elektron aber mit Lichtgeschwindigkeit, weil es masselos ist.
Dass das Elektron insgesamt nicht mit Lichtgeschwindigkeit von A nach B kommt, liegt an den vielen Zwischenstationen – das Elektron macht quasi Umwege:
Wir haben jetzt also ein Elektron, das lichtschnell ist, wenn man ganz genau hinguckt, aber nicht, wenn man nur guckt, welche Strecke es effektiv zurücklegt. Das ganze ist ein bisschen wie bei einem jungen Hund, der mit einem älteren Herrchen oder Frauchen unterwegs ist – er rast ständig hin und her, am Ende kommt er aber doch nur langsam vorwärts.
Hier stand ursprünglich ein Argument zur Impulserhaltung – nach längerem Nachdenken bin ich aber der Ansicht, dass es falsch ist.
An jedem dieser Kringel passiert dabei etwas seltsames: Die Elektronen wechseln ihre Helizität, die Zicks sind also immer linkshändig, die Zacks rechtshändig. Wenn man das so annimmt, dann kann man damit die Wechselwirkung zwischen Teilchen und den W- und Z-Bosonen korrekt beschreiben. Das Problem ist nur, dass Teilchen nicht “einfach so” ihre Helizität wechseln können. Rechnet man die Theorie in dieser Form zu Ende, ergeben sich jede Menge unsinniger Ergebnisse, vor allem ein Haufen Unendlichkeiten, die man auch mit mathematischer Trickserei nicht los wird. (Das hängt mit der so genannten “Eichsymmetrie” zusammen – in der jetzigen Form ist die Theorie nicht eichsymmetrisch. Eichtheorien habe ich hier erklärt. Und ich bin hier etwas schlampig – streng genommen muss man zwischen Helizität und Chiralität unterscheiden; für die Grundidee ist das nicht so wichtig, aber wer Details dazu wissen will, findet sie (auf Englisch) bei quantumdiaries.)
Endlich: Das Higgsfeld
Mit ein bisschen Cleverness können wir aber einen Mechanismus finden, der erklärt, was an den “Kringeln” passiert, ohne dass es zu diesem Problem kommt. Vergleicht nochmal das Bild mit einem Kringel mit dem Bild einer Wechselwirkung von oben:
Merkt ihr was? Wenn dort, wo der Kringel sitzt, in sozusagen “unsichtbares” Teilchen wäre, dann könnten wir unsere Kringel uminterpretieren, nämlich als Wechselwirkung (das zugehörige Teilchen hier in grün):
So sieht das dann für unser Elektron auf dem Weg von A nach B aus:
Damit das klappt, brauchen wir aber natürlich überall dort, wo so ein Kringel sitzen kann, ein passendes Teilchen zum Wechselwirken.1 Und da so ein Kringel überall sitzen kann und an jedem Kringel immer die gleiche Zahl – nämlich das m – dransteht, muss es immer und überall ein passendes Teilchen geben. Das ganze Universum muss also mit diesen Teilchen angefüllt sein, sie sind überall.
1Man könnte denken, das Elektron würde immer nur grüne Teilchen aussenden – aber dabei würde es ständig Energie verlieren, deshalb muss es ein grünes Teilchenfeld geben, mit dem das Elektron wechselwirken kann. Deswegen habe ich die Linien auch wieder wie oben horizontal gezeichnet.
Und – na klar – diese Teilchen sind die Higgs-Teilchen1. Weil sie überall gleichzeitig sind, spricht man auch vom Higgs-Feld. Ihr könnt euch das ein bisschen vorstellen wie die Luft um uns herum – wenn es keinen Wind und keine Luftbewegungen gäbe, sondern die wirklich überall und immer gleich wäre, dann würden wir von ihr nicht viel bemerken, aber sie würde trotzdem unsere Bewegung beeinflussen. (Das erinnert von der Idee her an die Dirac-See.) Ein anderes Bild ist das mit der Party, siehe den Link am Anfang des Artikels.
1Das ist jetzt ein bisschen vereinfacht, genau genommen sind sie es gerade nicht. Im zweiten Teil (seufz, erster Hauptsatz der Bloggodynamik: Blogartikel werden immer länger, als man denkt, selbst wenn man den 1. Hauptsatz berücksichtigt) erkläre ich den Unterschied zwischen Higgs-Feld und Higgs-Teilchen genauer.
Also: Statt einfach mit einer Masse m von A nach B zu fliegen, fliegen alle Teilchen mit Lichtgeschwindigkeit, aber immer im Zickzack. Immer wenn sie von einem Zick zu einem Zack wechseln, dann geschieht das durch Wechselwirkung mit dem Higgs-Feld. Dabei wechseln sie jedes Mal ihre Helizität.
Wie groß die Masse eines Teilchens ist, hängt jetzt davon ab, wie stark es mit dem Higgs-Feld wechselwirkt. Die Masse wird also einfach uminterpretiert, nämlich als Kopplung an ein überall vorhandenes Feld. Schwere Teilchen wie zum Beispiel top-Quarks koppeln also sehr stark an das Higgs-Feld, leichte Teilchen wie ein Neutrino (die ja vermutlich eine sehr kleine Masse haben) nur sehr schwach, masselose Teilchen wie Photonen gar nicht.
Mathematisch ist das ziemlich simpel: In der Lagrangedichte haben Masseterme die (vereinfachte, ich spare mir hier den ganzen Index-Spinoren-Sonstwas-Müll) Form m2φ2, Wechselwirkungsterme die Form g φ H φ – dabei ist φ das betrachtete Teilchen und H das Higgsfeld. g ist die Kopplung zwischen Higgsfeld und dem Feld φ. Ihr seht, dass die Uminterpretation mathematisch gar kein Problem ist.
Zwischenbilanz
Das ist also der Higgs-Mechanismus. Ich fasse die Ideen nochmal ganz kurz zusammen: Die schwache Kernkraft mit den W- und Z-Bosonen kann man korrekt nur beschreiben, wenn man annimmt, dass sich links- und rechtshändige Teilchen unterschiedlich verhalten. Weil man aber links- und rechtshändig durch bloßes Überholen ineinander überführen kann, lässt sich das nur realisieren, wenn die Materie-Teilchen “eigentlich” lichtschnell sind und nur im “Zickzack” fliegen. Die Zickzacks haben Kringel, an denen die Teilchen ihre Richtung wechseln. Und das wiederum können wir am besten dadurch beschreiben, dass an jedem dieser Kringel unser Teilchen mit einem anderen wechselwirkt – eben dem Higgsteilchen. Dazu muss der gesamte Raum mit einem Higgs-Feld angefüllt sein.
“Äh, ja, aber wenn dieses Higgsfeld immer überall ist, und wenn es sich dadurch äußert, dass es den Teilchen ihre Masse verleiht, was will man dann am CERN noch finden? ”
Gute Frage. Einfach gesprochen, kann man sagen, dass man zusätzliche Higgsteilchen erzeugen kann, solche, die sozusagen überschüssig sind – also quasi einen “Windstoß”.
Weniger einfach gesprochen ist es so, dass das nicht-verschwindende Higgs-Feld elementare Anregungen hat, die selbst wieder wie Teilchen aussehen. Um das zu verstehen, müssen wir uns fragen, wieso das Higgs-Feld eigentlich überall im Raum vorhanden sein soll – kostet sowas nicht extrem viel Energie?
Und das erkläre ich im zweiten Teil.






Kommentare (150)