In dieser Lücke plazieren wir jetzt unser zu versteckendes Ereignis. Anschließend durchläuft der Lichtstrahl wieder eine Glasfaser, die aber diesmal das umgekehrte Geschwindigkeitsverhältnis hat, so dass jetzt der vordere Teil gebremst und der hintere beschleunigt wird. Ist die Lücke wieder geschlossen, verschieben wir die Wellenlängen wieder passend so, dass eine ungestörte Welle entsteht:
Soweit das Prinzip. Die echte Kniffligkeit besteht natürlich vor allem darin, ein Lichtsignal passend aufzuspalten. Dazu nutzt man ein Gerät, das als “Zeitlinse” bezeichnet wird (genauer gesagt verwendet man halbierte Zeitlinsen, aber bevor ich das erkläre, kommt erst mal die ganze Zeitlinse). Da ich nicht so den Durchblick in Sachen Optik habe, sind die folgenden Erklärungen vermutlich etwas ungenau – wenn jemand von euch mehr Ahnung von Optik hat, tobt euch in den Kommentaren aus und ich korrigiere das hier entsprechend.
So wie normale Linsen Licht im Raum bündeln, bündeln Zeitlinsen Licht in der Zeit. Eine Linse fokussiert ja Lichtstrahlen auf einen Punkt im Raum (Bild von Wikipedia):

Von derivative work: Mouagip (talk) Sammellinse.png: Michael Schreiter Diese Vektorgrafik wurde mit dem Adobe Illustrator erstellt. – Sammellinse.png, CC BY-SA 3.0, Link
Damit kann man dann – das habt ihr sicher mal in der Schule gelernt – Lupen, Teleskope und Mikroskope bauen.
Eine Zeitlinse tut etwas Ähnliches. Sie “bündelt” einen Impuls in der Zeit – ein Lichtimpuls kann mit ihr zu einem kürzeren Impuls zusammengestaucht werden. Schematisch kann man das so zeichnen:
Dabei habe ich den Lichtimpuls als einfachen “Berg” gezeichnet. In Wahrheit besteht Licht aber ja aus Wellen – oder, anders gesagt, man kann jeden Lichtimpuls als Überlagerung von vielen Wellen darstellen. Das ist der Trick mit der Fourier-Transformation, den ich neulich in ganz anderem Zusammenhang schon mal erklärt habe.
Im Wellenbild bedeutet ein Zusammenstauchen des Impulses, dass wir mehr unterschiedliche Wellenlängen in das Lichtsignal einbauen müssen. Eine Zeitlinse modifiziert also einen Lichtimpuls, indem Anteile von Lichtwellen mit unterschiedlicher Wellenlänge hinzugefügt werden.
Wie ganz genau so eine “Zeitlinse” technisch funktioniert, habe ich nicht herausbekommen können – anscheinend schickt man das Lichtsignal in einen Wellenleiter (also einen leitenden Kanal), der aus Silizium gefertigt ist und einen Querschnitt von ein paar Hundert Nanometern hat (siehe z.B. hier). Die Mathematik dahinter ist auch nicht so ganz ohne…
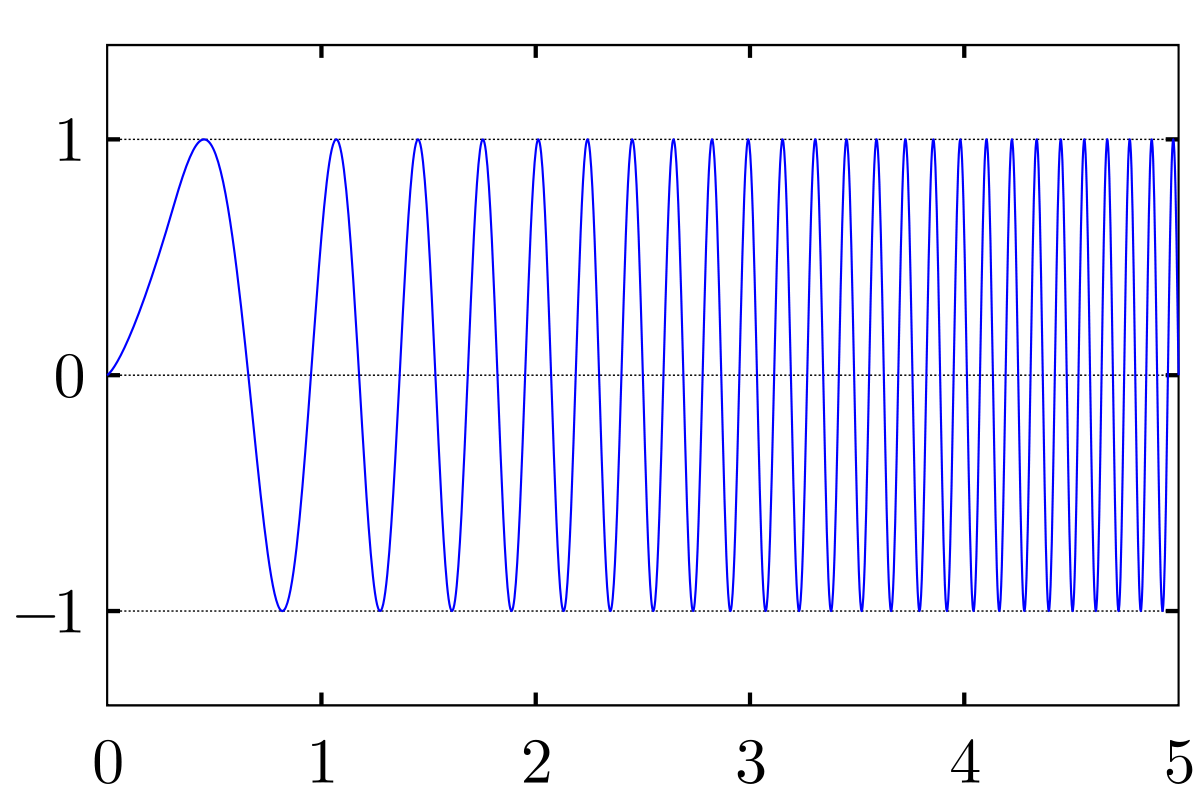
Was wir hier brauchen, ist eine “halbierte Zeitlinse” (auch da muss ich leider passen, was die technischen Details angeht). Sie verschiebt die Frequenz eines Signals ebenfalls, aber fügt nur entweder kürzere oder längere Wellenlängen hinzu. Aus einem Signal mit konstanter Wellenlänge wird ein sogenanntes “Chirp”-Signal (chirp=”tschilp”). Hier ein Bild von Wikipedia, das mehr sagt als tausend Worte:
Von Georg-Johann – Eigenes Werk, CC BY-SA 3.0, Link
Rechts im Bild ist die Frequenz hoch, dann wird sie kontrolliert niedriger (die Wellenlänge nimmt entsprechend zu).
Wir verwenden zwei solche “halbierte” Zeitlinsen, eine, die einen Teil des Signals kontrolliert zu längeren Wellenlängen verschiebt, eine, die das in Richtung kürzere Wellenlängen tut. Damit wird dann das zuvor gleichmäßig grüne Licht so verschoben, wie es oben im Teilbild b und f zu sehen ist. Der Rest ist dann “einfach” – wir brauchen nur die Glasfasern mit der passenden Dispersion.
Hier nochmal eine etwas andere Darstellung direkt aus der Veröffentlichung:
Oben seht ihr nochmal den Aufbau selbst – die Schleifchen stellen die Glasfaser dar, die Zahl (in Einheiten ps/nm) gibt die Stärke der Dispersion – also der Wellenlängenabhängigkeit der Lichtgeschwindigkeit – an und ist links und rechts des zu verbergenden Ereignisses genau entgegengesetzt. In der unteren Bildhälfte seht ihr die Frequenzdarstellung des Signals, die zeigt, wie es durch die halbierten Zeitlinsen aufgespalten wird und dann durch die unterschiedlichen Geschwindigkeiten die Lücke entsteht und am Ende wieder zusammengefügt wird.






Kommentare (19)