Als man nun versuchte, eine Theorie zu formulieren, die diese Eigenschaft hat und auch ansonsten zu den Beobachtungen passte, merkte man schnell, dass das nur dann funktioniert, wenn alle Teilchen masselos sind. Deswegen erfand man den Higgsmechanismus. (Dieses Erklärungsniveau entspricht ungefähr dem meiner Kurzerklärung. In der Langfassung habe ich auch noch ein bisschen erklärt, warum das so ist, warum also Teilchen in einer solchen Theorie masselos sein müssen.)
Verstehen, wie das Higgsteilchen prinzipiell wirkt
O.k., das Higgsfeld verleiht allen Elementarteilchen Masse. Aber wie funktioniert das? Wie kann die Wechselwirkung mit einem Feld so aussehen wie eine Masse, also für Phänomene wie die Trägheit sorgen?
Das zu verstehen beinhaltet zwei Bestandteile. Zum einen muss man verstehen, wie “Masse” sich überhaupt auf der Ebene der Elementarteilchen äußert.1 Dazu muss man ein bisschen tiefer in die Quantentheorie einsteigen. Dann sieht man, dass “Masse” sich in diesen Theorien in einer Weise äußert, die man grafisch so darstellen kann:
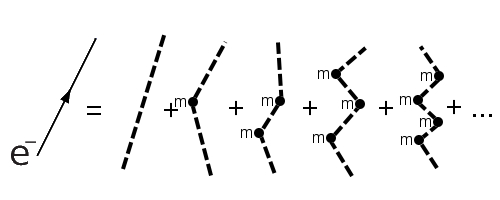
Hier fliegt links vom Gleichheitszeichen ein Elektron von A nach B. Man kann diesen Prozess auch darstellen wie auf der rechten Seite – dabei ist die gestrichelte Linie ein Elektron ohne Masse, und die kleinen Knubbel mit dem “m” dran sind eine grafische Darstellung dafür, wie die Masse hier eingeht. Eine weniger schwammige Erklärung des Bildchens findet ihr hier
1Dabei ist hier immer nur der Aspekt der Trägheit gemeint – wie Elementarteilchen mit Gravitationsfeldern wechselwirken, steht auf einem anderen Blatt, das wir leider noch nicht zu lesen bekommen haben, das ist die noch nicht gefundene Theorie der Quantengravitation.
Die Wechselwirkung mit dem Higgsfeld sieht jetzt ganz ähnlich aus (auch das erkläre ich etwas ausführlicher in der Langfassung des Higgs-Textes):
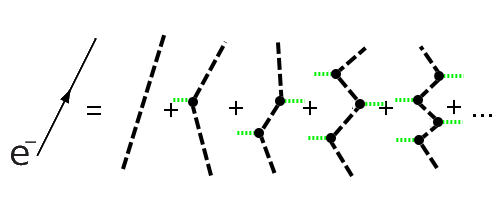
Statt der Knubbel mit dem Massenwert “m” dran haben wir jetzt eine Wechselwirkung mit dem (grün gestrichelten) Higgsfeld. Auf diesem Niveau hat man schon eine ganze Menge verstanden: Man sieht, dass die Wechselwirkung mit dem Higgsfeld wie eine Masse wirken kann und kann daraus folgern, dass die Stärke der Wechselwirkung mit dem Higgsfeld sagt, wie groß die Masse eines Teilchens ist.
Die Erklärung hier ist schon ziemlich involviert, kommt aber immer noch ohne viel Mathematik aus (und wer meine Quantenfeldtheorie-Serie gelesen hat, der sollte sie hoffentlich halbwegs nachvollziehen können). Die meisten PhysikerInnen würden aber sicher sagen, dass ein echtes Verständnis des Higgsfeldes nur auf mathematischer Ebene funktionieren kann.
Der nächste Schritt ist deshalb:
Verstehen, wie genau das Higgsfeld in dieser Weise wirken kann
Warum gerade ein Higgsfeld? Warum gibt es genau eine Anregung des Higgsfeldes, die man als Teilchen sehen kann, also nur eine Sorte Higgsteilchen? Wie passt das Higgsfeld genau in die Theorie und wie genau kann man mit dem Higgsfeld zum Beispiel die Masse von Teilchen berechnen? Wie stark ist das Higgsfeld?
Das sind alles Fragen, die man nur mit Hilfe der mathematischen Formulierung der Theorie beantworten kann. Wer dieses Niveau des Verstehens erreichen will, der muss deshalb mathematisch fit genug sein, um Gleichungen wie diese verstehen zu können:
Lagrangedichte des Standardmodells, von hier geklaut (ich übernehme keine Garantie, dass die Gleichung nicht etwas vereinfacht ist, ich habe nicht alle Terme geprüft).
Diese Stufe des Verständnisses ist sicherlich viel tiefer als die vorhergehenden, oder?
Das sollte zumindest so sein – die Erfahrung (auch meine eigene) zeigt aber, dass das nicht unbedingt so ist. Viele Lehrbücher und viele Profs in ihren Vorlesungen erklären nämlich überhaupt nur die Mathematik hinter solchen Theorien, ohne die Zusammenhänge auch anschaulich zu erklären. Das führt dazu, dass Physikstudis dann zwar die Gleichungen nachrechnen können, aber trotzdem nicht einfach oder anschaulich erklären können, was die Gleichungen aussagen. Das ging mir selbst während des Studiums manchmal auch so – ich konnte komplizierte Gleichungen nachrechnen, hatte aber kein wirkliches Verständnis für das, was die Gleichungen bedeuten, und hätte aus den Gleichungen deswegen Erklärungen wie die oben gegebenen nicht ableiten können. Das ist eins von vielen Beispielen für die oft furchtbar schlechte Didaktik der Physik.

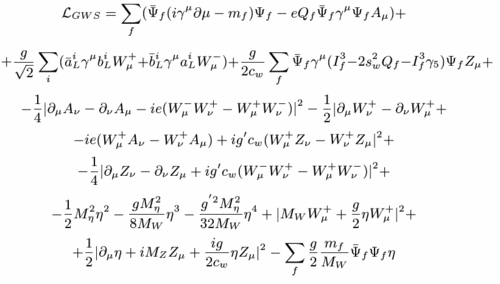





Kommentare (210)