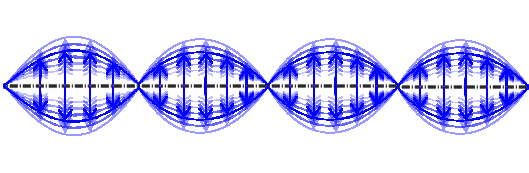
Ihr seht dabei auch, dass man sich ein einzelnes Photon eben gerade nicht als ein solches Wellenpaket mit klar definiertem elektrischen Feld vorstellen darf. Eine bessere Veranschaulichung eines einzelnen Photons sieht etwa so aus:
In blau habe ich wieder das elektrische Feld eingezeichnet, die Stärke des Farbtons soll die Wahrscheinlichkeit darstellen, diesen Wert des elektrischen Feldes zu messen. Wie ihr seht, ist ein einzelnes Photon in einem Überlagerungszustand aus unterschiedlichen Werten des elektrischen Feldes (warum das so ist, habe ich auch in der berühmten QFT-Serie erklärt).
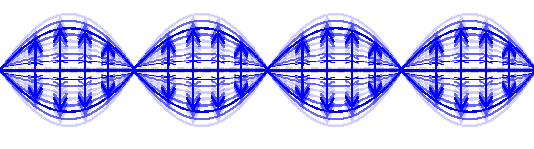
Ein Zustand mit zwei Photonen sieht dagegen beispielsweise so aus:
Jetzt haben wir eine hohe Wahrscheinlichkeit, ein elektrisches Feld zu finden, das mit einem bestimmten Wert nach oben zeigt, eine für ein Feld, das nach unten zeigt, und eine für ein feld mit Werten um Null – andere Werte des elektrischen Feldes sind nicht so wahrscheinlich.
Falls ihr das schwer verdaulich findet – keine Sorge, den meisten PhysikerInnen dürfte das ähnlich gehen. Für das Verständnis von Haroches Experiment sind die Details der Photonenzustände zum Glück nicht so wichtig, wichtig ist nur dass ihr folgendes verstanden habt: Haroche hat ein Wellenpaket zwischen seinen Spiegeln gespeichert, das in einem Überlagerungszustand aus unterschiedlichen Photonenzahlen vorliegt. Kohärente Zustände und Zustände mit einer genau definierten Zahl an Photonen sind also zueinander komplementär.
Photonen zählen
Unser Wellenpaket läuft jetzt also fröhlich zwischen den Spiegeln hin und her und stört sich nicht daran, dass es nicht weiß, aus wievielen Photonen es besteht (wahrscheinlich lesen Wellenpakete das vielgerühmte (von mir allerdings nur kurz angelesene und dann genervt zur Seite geworfene) Buch von Precht). Aber – wie ExperimentalphysikerInnen nun mal sind – Haroche lässt es nicht in Ruhe, sondern möchte es doch dazu zwingen, sich zu entscheiden, aus wie vielen Photonen es besteht. Nun, man könnte einfach einen empfindlichen Photodetektor zwischen die Spiegel schieben und die Energie der Photonen messen, aber dann wären sie leider absorbiert und somit nicht mehr vorhanden – das Ziel soll es aber sein, am Ende genau zu wissen, wie viele Photonen zwischen den Spiegeln sind.
Wie zählt man also die Photonen, ohne sie zu zerstören? Die Antwort ist einfach: Gaaanz vorsichtig 😉
Man verwendet hierzu speziell präparierte Atome, sogenannte Rydberg-Atome. In einem Rydberg-Atom ist eins der äußersten Elektronen in einem angeregten Zustand – wenn ihr euch der Einfachheit halber das Atom im guten alten Bohr-Modell vorstellt, dann kreist das Elektron auf einer Bahn sehr weit außen um den Atomkern. Im Experiment wurden Rubidium-Atome verwendet, bei denen ein Elektron auf der 50. oder 51. äußeren Schale liegt, die haben dann einen Radius von über Hundert Nanometern (normale Atomradien liegen im Bereich von Zehntel Nanometern.)
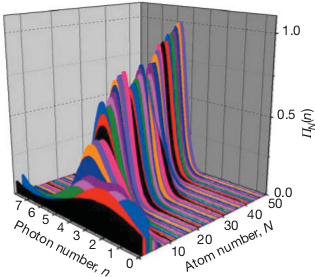
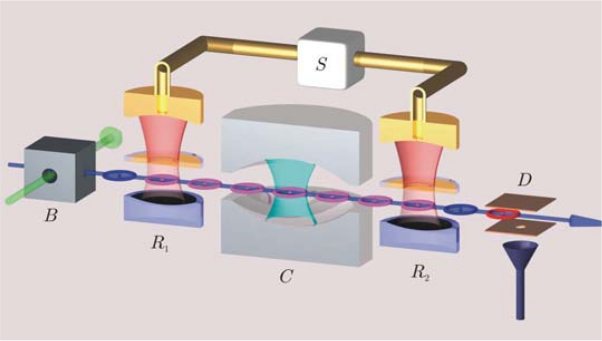
Hier mal ein Bild des Versuchsaufbaus (entnommen aus der “advanced information” zum Nobelpreis, Quelle s.u.):
Links bei B werden die Atome losgeschickt. Bei R1 werden die Atome in einen bestimmten Überlagerungszustand versetzt und dann bei R2 und bei D detektiert. Dazwischen liegt die “Kavität” C, also der Raum zwischen den Spiegeln, in dem sich die Photonen aufhalten.
Wenn ein so präpariertes Atom zwischen den Spiegeln hindurchläuft, dann beeinflussen die Photonen den Zustand des Atoms. Wie genau dieser Einfluss aussieht, hängt von der Zeit ab, die das Atom braucht, um den Raum zwischen den Spiegeln zu durchqueren, und vor allem von der Zahl der Photonen, mit denen das Atom wechselwirkt. (Die Photonen werden vom Atom aber nicht absorbiert, sondern ändern nur seine Energie ein wenig). Da die Photonenzahl aber in einem Überlagerungszustand ist, ist ja nicht eindeutig, mit wie vielen Photonen das Atom in Kontakt war, es ist jetzt also selbst auch in einem Überlagerungszustand (der Zustand der Photonen und der des Atoms sind also miteinander verschränkt, wie man quantenmechanisch sagt).






Kommentare (28)