Hand aufs Herz – hat irgendwer verstanden, wofür genau nun Haroche und Wineland ihren Nobelpreis bekommen haben? Irgendwas haben sie mit Quanteneffekten gemacht und die irgendwie gemessen, aber viel mehr als das ist den meisten Artikeln nicht zu entnehmen (eine lobenswerte Ausnahme ist dieser Artikel bei den scilogs – auch die Nobelpreis-Seite selbst ist ganz o.k., allerdings auf Englisch).
Damit ich zumindest eine Idee bekomme, worum es eigentlich geht, habe ich mir mal einen der Artikel von Haroche angeschaut. Fock-Zustände, kohärente Zustände, Rydberg-Atome, Quantum-non-demolition measurement, das sind nur einige der Fachbegriffe, mit denen da um sich geworfen wird. Aber keine Sorge, zumindest eine Idee, worum es geht, kann man schon bekommen, ohne Quantenoptik studiert zu haben.
Quantenzustände
Für den Anfang brauchen wir erst mal ein bisschen Grundwissen zur Quantenmechanik. Detailliert findet ihr das in diesem Blog ziemlich oft (zum Beispiel hier, hier, hier oder hier), deswegen gibt es hier nur eine Kurzfassung.
Objekte der klassischen Physik finden wir immer in bestimmten Zuständen – eine Snookerkugel beispielsweise hat einen bestimmten Ort und rollt mit einer bestimmten Geschwindigkeit, die den Zustand der Kugel angeben. (Ja, man könnte noch mehr zum Zustand sagen, zum Beispiel, dass auf der Kugel mal wieder nen Kreidefleck drauf ist oder sie eine Delle hat oder so, aber wir machen es jetzt nicht komplizierter als nötig.)
Objekte der Quantenmechanik haben auch Zustände. Auch eine Quanten-Snookerkugel kann beispielsweise einen bestimmten Ort haben, oder eine bestimmte Geschwindigkeit. Allerdings gibt es zwei fundamentale Unterschiede zur klassischen Physik:
Zum einen kann eine Quanten-Snookerkugel in einem Überlagerungszustand sein. Beispielsweise könnte sie in einem Zustand sein, bei dem sie sowohl auf dem grünen als auch auf dem braunen Spot des Snookertisches liegt. (Falls ihr – dann entgeht euch aber etwas – euch nicht für Snooker interessiert: Snooker ist Billard für Fortgeschrittene (ich hoffe, das lesen jetzt keine Poolspieler) und die farbigen “Spots” sind einfach bestimmte Punkte auf einem Snookertisch – die Regeln für Snooker habe ich übrigens auch mal erklärt.) Auch eine Quanten-Snookerkugel kann aber eine eindeutige Position haben, beispielsweise die auf dem grünen Spot. Eine solche eindeutige Position bekommt sie insbesondere dann, wenn ich ihren Ort tatsächlich messe (wenn ich also gucke, wo die Quantenkugel liegt) – ein Messprozess “zwingt” die Kugel in einen bestimmten Zustand. Messe ich den Ort, hat die Kugel hinterher tatsächlich einen bestimmten Ort, messe ich die Geschwindigkeit, hat die Kugel hinterher eine bestimmte Geschwindigkeit. (Wie wir gleich sehen werden, ist es meist in der Praxis nicht ganz so einfach…)
Der zweite Unterschied ist der, dass bestimmte Größen, die den Zustand beschreiben, nicht gleichzeitig einen eindeutigen Wert haben können. Das ist die berühmte Unschärferelation. Bestimme ich beispielsweise den Ort der Kugel durch eine Messung, dann befindet sie sich direkt nach dieser Ortsmessung in einem Zustand mit einem eindeutigen Ort, aber dafür mit einer vollkommen unbestimmten Geschwindigkeit. (Das bedeutet natürlich, dass die Kugel einen Moment höchstwahrscheinlich später nicht mehr am selben Ort sein wird.) Messe ich umgekehrt die Geschwindigkeit der Kugel, dann habe ich hinterher keinen Schimmer, wo sich die Kugel gerade aufhält. Größen wie Ort und Geschwindigkeit, die nicht gleichzeitig festgelegt sein können, heißen “komplementäre Größen”.
Um den Zustand einer Quanten-Snookerkugel vollständig zu beschreiben, entscheidet man sich für einen bestimmten Satz von Zustandsgrößen, die alle zueinander nicht komplementär sind. Beispielsweise also den Ort oder die Geschwindigkeit (aber eben nicht beides). Man gibt dann die Wahrscheinlichkeit (genauer gesagt, die Wahrscheinlichkeitsamplitude, aber wir wollen mal nicht so pingelig sein) für jeden denkbaren Messwert in diesem Satz von Zustandsgrößen an. Also beispielsweise: 1% Wahrscheinlichkeit für den grünen Spot, 2% Wahrscheinlichkeit für den braunen Spot ,10% Wahrscheinlichkeit direkt vor der gelben Ecktasche (freu…) usw. Alternativ kann man dasselbe auch für die Geschwindigkeiten machen und angeben: 3% Wahrscheinlichkeit für eine Geschwindigkeit in Richtung der linken Mitteltasche usw usf. Wer Physik studiert und fleißig Übungsaufgaben rechnet, der kann auch zwischen diesen beiden Beschreibungen hin- und herrechnen: wenn ich also die Wahrscheinlichkeit dafür weiß, mit der die Kugel an jedem beliebigen Punkt des Tisches ist, dann kann ich ausrechnen, welche Wahrscheinlichkeit eine bestimmte Geschwindigkeit hat. Anders als in der klassischen Physik sind diese Größen also nicht unabhängig. (Eine Kugel in der klassischen Physik kann eindeutig auf dem gelben Spot liegen und in jede beliebige Richtung laufen, aber eine Quanten-Snookerkugel, die eindeutig auf dem gelben Spot liegt, kann nicht in eine bestimmte Richtung laufen – vielmehr sind alle Richtungen gleichwahrscheinlich (das dürfte Quanten-Snooker zu einer ziemlich kinffligen Sportart machen…).)
Zerstörungsfreie Quantenmessungen
Wie oben angeführt, befindet sich ein Quantensystem nach einer Messung in einem eindeutigen Zustand zur jeweiligen Messgröße. Messe ich also den Ort der Snookerkugel, dann ist die Snookerkugel an diesem Ort. Gleiches gilt für die Geschwindigkeit. Das ist allerdings meist nur in der Theorie sie. Schon bei der Ortsmessung haben wir gesehen, dass die Kugel ja nicht am Ort bleibt, sondern – weil ihre Geschwindigkeit unbestimmt ist – nach kurzer Zeit irgendwo sein wird. Messe ich beispielsweise ein Lichtteilchen (ein Photon), dann tue ich das vielleicht mit einer Fotoplatte – nach der Ortsmessung ist deshalb das Photon zerstört. In der Realität ist es deshalb sehr knifflig, einen Quantenzustand so zu messen, dass das Teilchen hinterher immer noch in diesem Zustand ist, den ich jetzt genau kenne. Das Team um Haroche hat genau solche Messungen (“quantum non-demolition measurement”, zu deutsch etwa “zerstörungsfreie Quantenmessung”) hinbekommen.
Allerdings haben sie dazu keine Snookerkugeln genommen (wer es schafft, die in einen messbaren Überlagerungszustand zu versetzen, bekommt bestimmt auch nen Nobelpreis), sondern mit Licht. Licht hat allerdings den Nachteil, dass es sich mit Lichtgeschwindigkeit bewegt, und die ist ziemlich groß. Um am Licht rumzumessen, haben Haroche und sein Team deshalb das Licht eingesperrt, und zwar zwischen zwei Spiegel. Dazwischen kann das Licht “gefangen” werden. (Das sind allerdings keine handelsüblichen Badezimmerspiegel aus dem Baumarkt, sondern extrem stark gekühlte supraleitende Spiegel, denn das Licht soll für eine Zehntelsekunde zwischen den Spiegeln bleiben – dabei wird es natürlich sehr oft “hin- und her-reflektiert”, so dass man Spiegel braucht, die möglichst absolut überhaupt kein Licht verschlucken.)
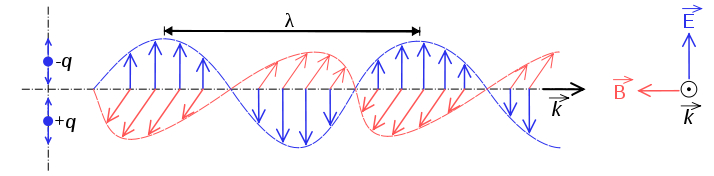
Wir betrachten das ganze erst mal mit den Augen der klassischen Physik. Danach ist Licht ja eine elektromagnetische Welle, die man sich etwa so vorstellen kann:
In blau seht ihr hier das elektrische Feld, in rot das Magnetfeld, und die Welle bewegt sich von links nach rechts. In diesem Zustand ist das elektrische Feld der Welle eindeutig festgelegt und zeigt immer in eine bestimmte Richtung, hier zeigt es im linken Wellenberg zum Beispiel nach oben, im nächsten nach unten. Licht, bei dem das so ist, nennt man kohärent – es ist die Art Licht, die man aus einem Laser herausbekommt.
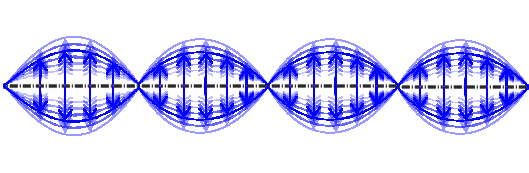
Im Experiment von Haroche wurde jetzt eine solche Welle zwischen den Spiegeln gefangen, und zwar so, dass es nur ein kleines Wellenpaket war, das zwischen den Spiegel hin- und herläuft. Unser Licht ist jetzt also in einem kohärenten Zustand, und zwar auch, wenn man es quantenmechanisch beschreibt. So etwa könnt ihr euch das elektrische Feld in so einem Wellenpaket vorstellen:
Das Wellenpaket läuft dabei so zwischen den beiden Spiegeln hin und her, dass an einem bestimmten Ort das elektrische Feld immer denselben Wert hat – wenn ihr euch vorstellt, dass oben im Bild recht der eine und links der andere Spiegel ist, dann sieht das Wellenpaket, wenn es nach einem hin und her wieder an derselben Stelle angekommen ist, auch wieder genauso aus.
Wie viele Photonen?
Ein solcher kohärenter Zustand hat eine sehr merkwürdige Eigenschaft: Seine Energie ist nämlich nicht exakt definiert. Die Energie ist eine klassische Messgröße, aber genau wie oben unsere Snookerkugel in einem Überlagerungszustand aus unterschiedlichen Geschwindigkeiten war, ist unser kohärentes Wellenpaket in einem Überlagerungszustand aus unterschiedlichen Energien.
Nun besteht Licht ja – in der quantenmechanischen Betrachtungsweise – aus Lichtteilchen, den Photonen. Jedes Photon (mit einer bestimmten Wellenlänge) trägt auch eine bestimmte Energie. Wenn also die Energie des Wellenpakets nicht genau definiert ist, sondern es sich in einem Überlagerungszustand befindet, dann heißt das, dass die Zahl der Photonen in diesem Wellenpaket ebenfalls nicht genau definiert ist. Das Paket ist in einem Überlagerungszustand aus null, einem, zwei, drei, usw. Photonen. (Für die Handvoll Leute, die fleißig meine Quantenfeldtheorie-Serie gelesen hat, ist das natürlich ein alter Hut.)
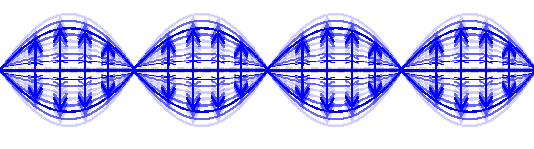
Ihr seht dabei auch, dass man sich ein einzelnes Photon eben gerade nicht als ein solches Wellenpaket mit klar definiertem elektrischen Feld vorstellen darf. Eine bessere Veranschaulichung eines einzelnen Photons sieht etwa so aus:
In blau habe ich wieder das elektrische Feld eingezeichnet, die Stärke des Farbtons soll die Wahrscheinlichkeit darstellen, diesen Wert des elektrischen Feldes zu messen. Wie ihr seht, ist ein einzelnes Photon in einem Überlagerungszustand aus unterschiedlichen Werten des elektrischen Feldes (warum das so ist, habe ich auch in der berühmten QFT-Serie erklärt).
Ein Zustand mit zwei Photonen sieht dagegen beispielsweise so aus:
Jetzt haben wir eine hohe Wahrscheinlichkeit, ein elektrisches Feld zu finden, das mit einem bestimmten Wert nach oben zeigt, eine für ein Feld, das nach unten zeigt, und eine für ein feld mit Werten um Null – andere Werte des elektrischen Feldes sind nicht so wahrscheinlich.
Falls ihr das schwer verdaulich findet – keine Sorge, den meisten PhysikerInnen dürfte das ähnlich gehen. Für das Verständnis von Haroches Experiment sind die Details der Photonenzustände zum Glück nicht so wichtig, wichtig ist nur dass ihr folgendes verstanden habt: Haroche hat ein Wellenpaket zwischen seinen Spiegeln gespeichert, das in einem Überlagerungszustand aus unterschiedlichen Photonenzahlen vorliegt. Kohärente Zustände und Zustände mit einer genau definierten Zahl an Photonen sind also zueinander komplementär.
Photonen zählen
Unser Wellenpaket läuft jetzt also fröhlich zwischen den Spiegeln hin und her und stört sich nicht daran, dass es nicht weiß, aus wievielen Photonen es besteht (wahrscheinlich lesen Wellenpakete das vielgerühmte (von mir allerdings nur kurz angelesene und dann genervt zur Seite geworfene) Buch von Precht). Aber – wie ExperimentalphysikerInnen nun mal sind – Haroche lässt es nicht in Ruhe, sondern möchte es doch dazu zwingen, sich zu entscheiden, aus wie vielen Photonen es besteht. Nun, man könnte einfach einen empfindlichen Photodetektor zwischen die Spiegel schieben und die Energie der Photonen messen, aber dann wären sie leider absorbiert und somit nicht mehr vorhanden – das Ziel soll es aber sein, am Ende genau zu wissen, wie viele Photonen zwischen den Spiegeln sind.
Wie zählt man also die Photonen, ohne sie zu zerstören? Die Antwort ist einfach: Gaaanz vorsichtig 😉
Man verwendet hierzu speziell präparierte Atome, sogenannte Rydberg-Atome. In einem Rydberg-Atom ist eins der äußersten Elektronen in einem angeregten Zustand – wenn ihr euch der Einfachheit halber das Atom im guten alten Bohr-Modell vorstellt, dann kreist das Elektron auf einer Bahn sehr weit außen um den Atomkern. Im Experiment wurden Rubidium-Atome verwendet, bei denen ein Elektron auf der 50. oder 51. äußeren Schale liegt, die haben dann einen Radius von über Hundert Nanometern (normale Atomradien liegen im Bereich von Zehntel Nanometern.)
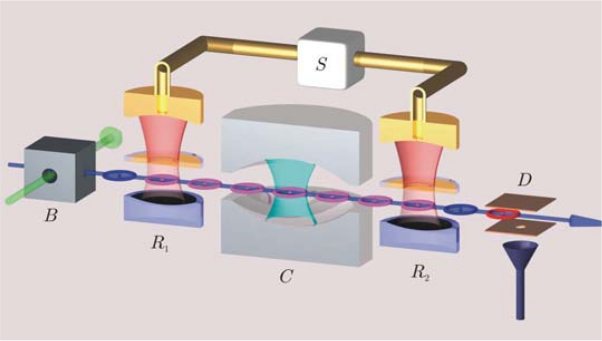
Hier mal ein Bild des Versuchsaufbaus (entnommen aus der “advanced information” zum Nobelpreis, Quelle s.u.):
Links bei B werden die Atome losgeschickt. Bei R1 werden die Atome in einen bestimmten Überlagerungszustand versetzt und dann bei R2 und bei D detektiert. Dazwischen liegt die “Kavität” C, also der Raum zwischen den Spiegeln, in dem sich die Photonen aufhalten.
Wenn ein so präpariertes Atom zwischen den Spiegeln hindurchläuft, dann beeinflussen die Photonen den Zustand des Atoms. Wie genau dieser Einfluss aussieht, hängt von der Zeit ab, die das Atom braucht, um den Raum zwischen den Spiegeln zu durchqueren, und vor allem von der Zahl der Photonen, mit denen das Atom wechselwirkt. (Die Photonen werden vom Atom aber nicht absorbiert, sondern ändern nur seine Energie ein wenig). Da die Photonenzahl aber in einem Überlagerungszustand ist, ist ja nicht eindeutig, mit wie vielen Photonen das Atom in Kontakt war, es ist jetzt also selbst auch in einem Überlagerungszustand (der Zustand der Photonen und der des Atoms sind also miteinander verschränkt, wie man quantenmechanisch sagt).
Misst man hinterher den Spin (also den Drehimpuls) des Atoms, so kann man daraus Rückschlüsse auf die Zahl der Photonen ziehen. Allerdings ist es nicht so, dass eine einzelne Messung eines Atoms die Zahl der Photonen eindeutig festlegt. Jede Messung eines Atoms gibt einem ein kleines Stückchen Information über die Zahl der Photonen. Schickt man ein Atom nach dem anderen zwischen den Spiegel hindurch, so wird der Zustand der Photonen langsam aber sicher in Richtung auf eine bestimmte Photonenzahl geschoben. (Ich erspare es euch und mir, hier die genaue Herleitung hinzuschreiben, die habe ich mir auch nicht im Detail angetan.)
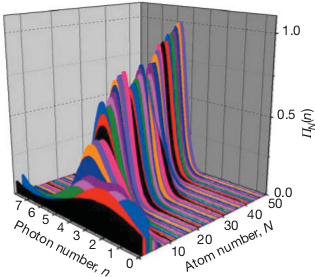
So sieht das ganze in der Messung am Ende aus:
Auf der einen Achse seht ihr die Zahl der Photonen, auf der zweiten die Zahl der durchgeschickten Atome. Die senkrechte Richtung sagt, wie wahrscheinlich eine bestimmte Photonenzahl ist. Am Anfang ist die Photonenzahl sehr unscharf, mit einem Maximum etwa bei drei Photonen (die flache schwarze Kurve). Je mehr Photonen gemessen werden, desto stärker zieht sich die Verteilung zusammen und endet schließlich mit einem Maximum bei einer bestimmten Photonenzahl – hier im Bild sind es 5 Photonen.
Am Ende wissen wir also, dass genau 5 Photonen zwischen den Spiegeln hin- und herflitzen, die dafür aber natürlich nicht mehr in einem kohärenten Zustand sind. Während die Photonenzahl immer eindeutiger wird, gerät das System in komplizierte Überlagerungszustände, die teilkohärent sind, bei denen also einige Werte des elektrischen Feldes ausgeschlossen sind, andere nicht. In anderen Arbeiten haben Haroche und sein Team, wenn ich es richtig verstehe, einen Zustand gebaut, in dem das elektrische Feld in einem Überlagerungszustand aus zwei entgegengesetzten Werten war. Mit dem raffinierten Versuchsaufbau lassen sich also verschiedenste Quantenzustände präparieren und untersuchen. Natürlich wird in den Medien immer viel über mögliche Anwendungen in Quantencomputern gesprochen – Anwendungen sind ja immer wichtig. Ich finde aber die subtile Überlagerung von Quantenzuständen und ihre Messung eigentlich viel schicker…
Scientific Background on the Nobel Prize in Physics 2012, “measuring and manipulating individual quantum systems”
compiled by the Class for Physics of the Royal Swedish Academy of Sciences
PS: Der Titel des Textes ist eine (vermutlich ziemlich nerdige) Anspielung auf D. Zindells Frage “How do you capture a beautiful bird without killing its spirit?” (in der Trilogie “A requiem for homo sapiens”).







Kommentare (28)