Anschließend können Frauen als Großmütter tätig werden und ihre Enkel versorgen, allerdings nur bis zu einem Alter, bei dem sie zu gebrechlich dafür werden. Anders als in früheren Modellen kann in diesem Modell hier jede Großmutter nur ein einziges Kind versorgen (was sicher eine sehr vorsichtige Annahme ist).
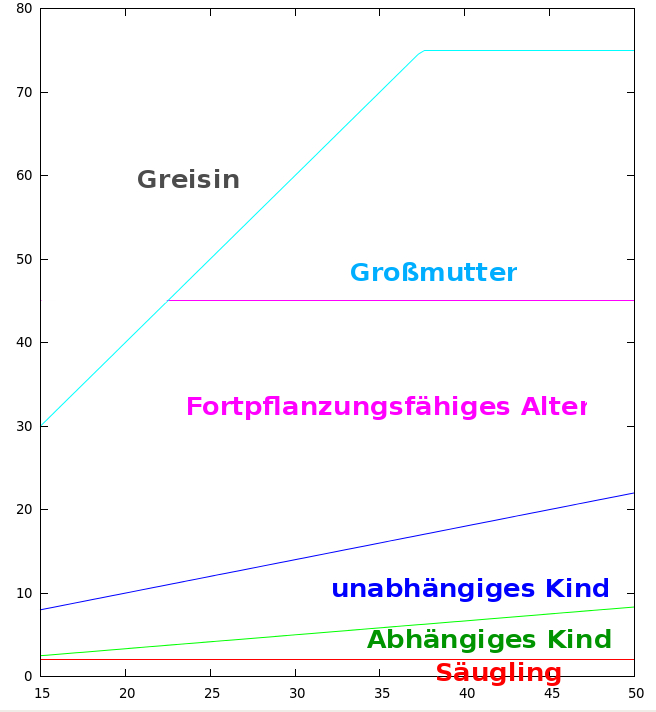
Wie lange die einzelnen Phasen dauern, hängt in diesem Modell von der Lebensdauer ab (also dem Parameter, den ich oben erklärt habe). Weil die Tabellen im paper etwas unübersichtlich sind, habe ich das in einer Grafik zusammengefasst:
Die Säuglingsphase dauert immer zwei Jahre. Je größer die Lebenserwartung ist, desto länger dauert es dann bis zur Unabhängigkeit und zum Erwachsenwerden und bis zum Greisenalter. (Das ist allerdings bei 75 Jahren “gedeckelt”.) Man mag jetzt einwenden, dass natürlich eine längere Lebenserwartung dann auch dadurch getrieben werden könnte, dass eine längere Jugend einen evolutionären Vorteil bietet, das ist hier im Modell aber nicht berücksichtigt worden, hier geht es nur um die Frage, ob Großmütter durch Versorgen von Kindern die Lebensdauer zu größeren Werten verschieben.
Jetzt können wir das System simulieren: Dazu starten wir mit z.B. 1000 Individuen mit bestimmter Lebensdauer und schauen, wie sich die Population Zeitschritt für Zeitschritt entwickelt. Will man das für sehr viele verschiedene Varianten und lange Zeiträume machen, dann wird es allerdings sehr rechenaufwändig. Die AutorInnen der Arbeit waren deshalb schlau, und haben ihr Modell mathematisch in Form von Differentialgleichungen umgeschrieben, die sich deutlich schneller lösen lassen.
Als Ergebnis schaut man sich die Reproduktionsrate an: Wie stark wächst die Population maximal pro Jahr? (Es ist im paper nicht genau erklärt, aber ich gehe davon aus, dass es sich bei der Reproduktionsrate um das Netto-Wachstum handelt, also Zahl der Geburten minus Zahl der Todesfälle.)
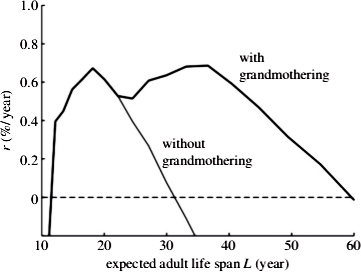
Aus Kim et al, s.u.
Hier ist also aufgetragen um wie viel Prozent die Population pro Jahr wachsen kann. Bei zu kurzer Lebenserwartung wächst die Population nur langsam oder schrumpft sogar – das liegt sicherlich daran, dass dann zwei Jahre bis zum Abstillen sehr lang sind (und hinzu kommt ja noch ein Jahr bis zur nächsten Geburt). Ein Maximum erreicht die Kurve bei einer Lebenserwartung von 18 Jahren, anschließend fällt sie wieder ab. Dieser Abfall liegt laut dem paper am zunehmenden Alter bei der ersten Geburt – ich denke, dass hier auch hinzukommt, dass immer mehr Frauen die 45-Jahre-Grenze erreichen, ab der sie keine Kinder mehr bekommen können. Einen Großmutter-Effekt gibt es hier noch nicht, weil das Minimum-Alter fürs “großmuttern” von 45 Jahren noch oberhalb der Schwelle zum Greisinnenalter liegt. (Was mir aus dem paper nicht ganz klar wird, ist, ob bei dieser Lebenserwartung von z.B. 20 Jahren eine Frau über 40 – die ja schon Greisin ist – noch Kinder bekommen kann.)
Ab einer Lebenserwartung von 22,5 Jahren können dann Frauen über 45 als Großmütter agieren (sie dürfen ein einmal übernommenes Kind auch weiter betreuen, selbst wenn sie das Greisinnen-Alter erreichen). Und hier sieht man dann sofort einen drastischen Effekt durch das Wirken der Großmütter: Die Kurve mit Großmutter-Efekt schnellt wieder nach oben und erreicht ein zweites Maximum bei einem Alter von 37 Jahren und auch bei sehr hoher Lebenserwartung bleibt die Reproduktionsrate positiv. Es zeigt sich also ein deutlicher Großmutter-Effekt.
Aber kann ein solcher Großmutter-Effekt sich auch evolutionär durchsetzen? Um das zu prüfen, wurde zusätzlich Evolution eingebaut: Jedes Kind bekommt zunächst als Lebenserwartungsparameter den Mittelwert aus den Parametern der Eltern, doch dieser Wert kann durch Mutation noch nach oben oder unten verschoben werden. Weiterhin wurde angenommen, dass der Lebensraum der betrachteten Gruppe Platz für maximal 1000 Menschen liefert. Wenn es mehr als 1000 Menschen gibt, dann sterben im nächsten Simulationszeitraum (typischerweise 3 Monate) so viele Menschen zufällig, dass die Zahl 1000 wieder erreicht wird.






Kommentare (15)