|QM-Zustand> = a |hier> + b |da>,
aber a und b sind jetzt nicht einfach 1 oder 0, sondern sind jetzt beliebige Zahlen, die lediglich folgende Eigenschaft erfüllen müssen:
a²+b²=1
Der klassische Zustand mit a=1,b=0 (oder umgekehrt) erfüllt diese Regel, er ist also auch in der QM ein zulässiger Zustand. In der Quantenmechanik allerdings wäre auch a=b=1/√2 ein erlaubter Zustand, denn dann ist
Genau genommen sind die Zahlen a und b komplexe Zahlen, keine gewöhnlichen reellen Zahlen. Diese kleine Komplikation spielt hier erst einmal keine Rolle, deswegen verbanne ich sie hinter dieses Warnschild. Komplexe Zahlen habe ich mal ausführlich hier erklärt.
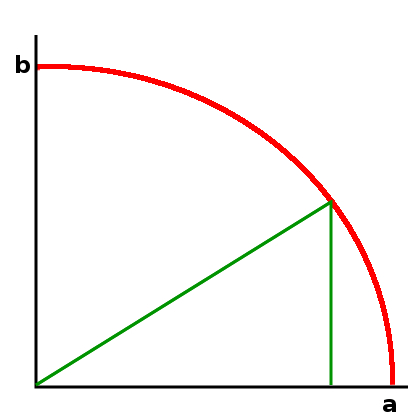
Man kann sich die Extra-Bedingung für a und b auch leicht grafisch veranschaulichen: a²+b²=1 ist gerade die Formel für einen Kreis mit Radius 1:
In der klassischen Physik sind also nur die beiden Zustände auf den Achsen erlaubt (a=1, b=0 und umgekehrt), aber ein quantenmechanischer Zustand kann sich irgendwo auf der roten Linie befinden. Es gibt also in der Quantenmechanik unendlich viele verschiedene Möglichkeiten für ein System, dass klassisch nur zwei mögliche Zustände hat. (Und das ist auch genau der Grund, warum so viel über Quantencomputer geredet wird: Ein klassisches Bit hat entweder den Wert 0 oder den Wert 1, ein qu-bit dagegen kann sich in allen möglichen Überlagerungszuständen befinden.) Diese einfache grafische Darstellung ist allerdings nur bei einem Zwei-Zustands-System wirklich hilfreich (und auch da ist sie nicht ganz exakt, weil – wie oben hinter dem Warnschild erläutert – a und b komplexe Zahlen sein können). Deswegen wird sie in dieser Form selten angewandt, zur Illustration des Unterschieds zwischen einem klassischen und einem Qm-System ist sie aber trotzdem hilfreich.
Wenn unser Teilchen an drei Orten sein kann (also auch noch |dort>), dann sieht der Zustand entsprechend aus:
|QM-Zustand> = a |hier> + b |da> + c | dort>,
und jetzt gilt ganz entsprechend
a²+b²+c²=1 (Das könnte man grafisch mit einer Kugel veranschaulichen, wenn man will…)
Fazit: Ein quantenmechanisches System kann sich in einer Überlagerung aus unterschiedlichen Zuständen befinden.
Die Zahlen a,b,c usw. nennt man die Wahrscheinlichkeitsamplitude des jeweiligen Zustands. In meiner Formel oben ist a also die Wahrscheinlichkeitsamplitude für den Zustand |hier>, b die für den Zustand |da>. In der klassischen Physik ist eine der Wahrscheinlichkeitsamplituden gleich eins, alle anderen sind null, deswegen ergibt diese Zustands-Schreiberei nicht viel Sinn. In der QM allerdings sind beliebige Werte für die Wahrscheinlichkeitsamplituden möglich (allerdings muss die obige Formel gelten: Die Summe der Quadrate aller Amplituden muss genau eins ergeben, warum, sehen wir noch).
Bevor es weitergeht, hier eine kleine Übung, damit ihr seht, ob ihr auch alles bis hier verstanden habt:
Ein quantenmechanisches Teilchen soll sich in einem von 4 möglichen Zuständen befinden können, die wir von |1> bis |4> durchnummerieren. Welcher der folgenden Zustände ist möglich, welcher nicht:
a) Ist möglich, denn (1/2)²=1/4, die Summe aller vier Amplitudenquadrate ist also gleich 1.
b) Ist auch möglich, denn die Summe der Amplitudenquadrate ist wieder gleich 1 – die Amplituden für die Zustände |2> und |4> sind gleich Null.
c) Hier werden zwei Zustände multipliziert. Das ist so nicht möglich, die unterschiedlichen Zustände müssen immer addiert werden. (Wenn man allerdings mehrere Teilchen betrachtet, kann man diese Schreibweise verwenden, sie besagt dann, dass sich das eine Teilchen im Zustand |1> und das andere im Zustand |2> befindet.)
d) Das geht auch nicht, den die Summe der Quadrate der Amplituden ist 7/9, also nicht gleich 1.
Die Bedeutung der Überlagerung
O.k., wir haben gesehen, dass ein Teilchen (oder überhaupt jedes quantenmechanische System) sich in einem Überlagerungszustand befinden kann. Aber was bedeutet das? Wir beobachten ja keine Objekte, die gleichzeitig hier und da sind – wenn ich hinschaue, ist meine Computertastatur genau an einer Stelle, sonst wäre das Tippen von Blogtexten auch ziemlich schwierig.







Kommentare (197)