Im zweiten Teil der Quantenmechanik-Reihe schauen wir uns die Zustände eines Teilchens noch etwas genauer an.
Was ist ein Zustand?
Bisher habe ich immer nur von Teilchen gesprochen, die irgendwo sind (oder manchmal auch irgendwo nicht sind). Der Zustand eines Teilchens war also immer durch seinen Ort gekennzeichnet. Im klassischen Fall war der Ort eindeutig, in der QM konnte der Zustand aber eine Überlagerung verschiedener Orte sein. Wenn ich das Teilchen an einem Ort messe, dann ist es hinterher in dem entsprechenden Zustand.
Nicht alle Zustände sind aber Ortszustände (obwohl das Teilchen natürlich immer irgendwo sein muss). Man kann ja auch andere Eigenschaften von Teilchen messen – dann sind sie hinterher ebenfalls in einem bestimmten Zustand, aber dieser Zustand ist nicht unbedingt einer mit einem eindeutigen Ort. Ging das zu schnell? Keine Sorge, wie das genau geht, schauen wir uns jetzt an.
Dazu betrachten wir ein (hier etwas vereinfachtes) Beispiel, nämlich das einfachste denkbare Molekül.
Dazu brauchen wir zunächst mal ein Wasserstoffatom. Das besteht aus einem Proton und einem Elektron. Das Proton ist knapp 2000 mal schwerer als das Elektron und ich tue hier so, als wäre es unendlich schwer und müsste nicht mit den Mitteln der Qm beschrieben werden. Wir müssen uns also nur um das Elektron kümmern. Das Elektron ist elektrisch negativ geladen und wird vom Proton angezogen. Es nähert sich deshalb dem Proton an und hält sich bevorzugt in seiner Nähe auf. Im Zustand mit der niedrigsten Energie sieht seine Wellenfunktion etwa so aus:
Dabei habe ich den Wert der Wellenfunktion entlang einer Linie aufgetragen, die durch das Proton geht. (Es gibt auch dreidimensionale Darstellungen, aber dann wird das, was gleich kommt, sehr unübersichtlich.) Da, wo die Funktion ihr Maximum hat, sitzt genau das Proton. Das Elektron ist also bevorzugt dicht ans Proton gekuschelt (seine Wahrscheinlichkeit ist dort besonders hoch), aber auch nicht zu dicht.
Aber keine Sorge, wir brauchen uns um die Details der Wellenfunktion im Moment nicht zu kümmern (die Bilder hier sind eh nur qualitativ richtig). Solange das Elektron im energetisch günstigsten Zustand (dem Grundzustand) ist, hält es sich möglichst dicht am Proton auf, das ist eigentlich alles, was uns im Moment interessiert. Wir haben also einen Zustand des Elektrons, nämlich den Grundzustand an diesem Proton.
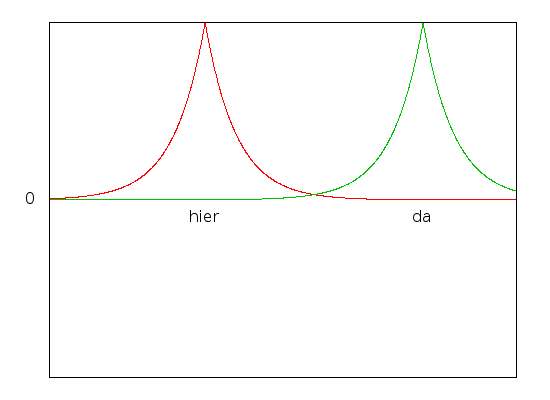
Jetzt bringen wir ein zweites Proton ins Spiel. Nehmen wir erstmal an, das Proton wäre sehr weit vom ersten weg. Unser Elektron kann jetzt entweder beim Proton “hier” sein oder beim Proton “da”:
Wir könnten das messen, indem wir z.B. die elektrische Ladung messen – ist das Elektron beim Proton “hier”, dann haben wir “hier” ein neutrales Wasserstoffatom und “da” ein geladenes Proton. Das ist also genau die Situation vom letzten Mal, bei der wir ja mit zwei Zuständen |hier> und |da> angefangen haben.
Wir haben beim letzten Mal auch gesehen, dass wir beliebige Misch-Zustände aus |hier> und |da> haben können – der allgemeine Zustand ist
a|hier> + b |da> mit der Bedingung a²+b²=1.
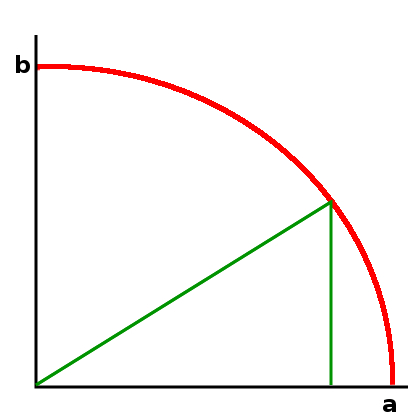
Grafisch habe ich das mit diesem Bild veranschaulicht:
Dahinter steckt übrigens – falls ihr es nicht gemerkt habt – der Satz des Pythagoras: Das eingezeichnete grüne Dreieck ist ja rechtwinklig, und ihr habt sicher mal die Formel a²+b²=c² lernen (und vielleicht auch beweisen) müssen. Die Länge c ist hier gerade gleich 1, weil die Summe unserer Wahrscheinlichkeiten ja 1 sein soll.
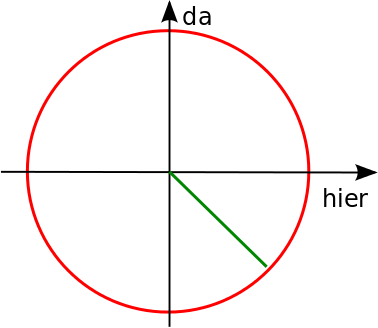
Dabei war ich zugegebenermaßen etwas schlampig, denn a und b können auch negativ sein. Eigentlich müsste das Bild also so aussehen (diesmal mit inkscape statt gimp gezeichnet, das muss ich eh mal lernen):
Dabei habe ich die Achsen jetzt mit “hier” und “da” beschriftet, nicht mit den Zeichen für die Koeffizienten, weil das dann später übersichtlicher wird, wenn wir noch mehr Achsen einführen.







Kommentare (53)