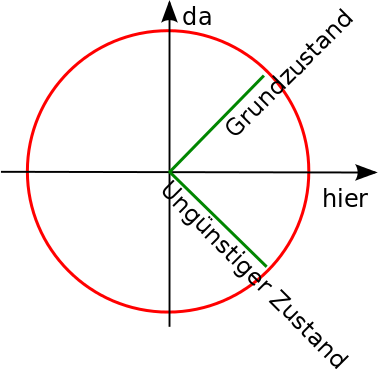
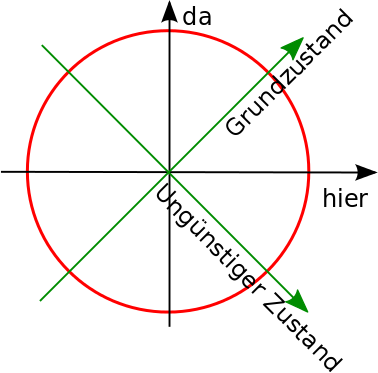
Kleine Aufgabe: welchen Zustand habe ich in grün oben eingezeichnet?
Antwort: Der Zustand liegt unter 45°, also ist der Anteil von “hier” und “da” gleich groß, der “da”-Anteil ist aber negativ (er geht ja nach unten). Der Zustand ist also
Das ist auch ein erlaubter Zustand, denn beim Quadrieren fällt das Minuszeichen ja weg.
Unser Elektron kann also in einem beliebigen Mischzustand zwischen |hier> und |da> sein, so wie bisher auch.
Interessant wird die Sache, wenn wir unsere beiden Protonen einander annähern. Dann ist es für das Elektron energetisch günstiger, sich in der Mitte zwischen den beiden Protonen aufzuhalten als weiter außen, weil sich dort die elektrische Anziehung der beiden Protonen überlagert. Der energetisch günstigste Zustand ist der, bei dem die beiden Zustände addiert werden:
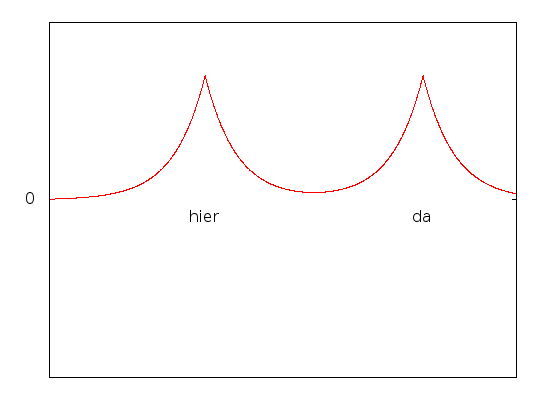
Dieser Zustand ist der Grundzustand, also der mit der niedrigsten Energie. Die zugehörige Wellenfunktion sieht etwa so aus:
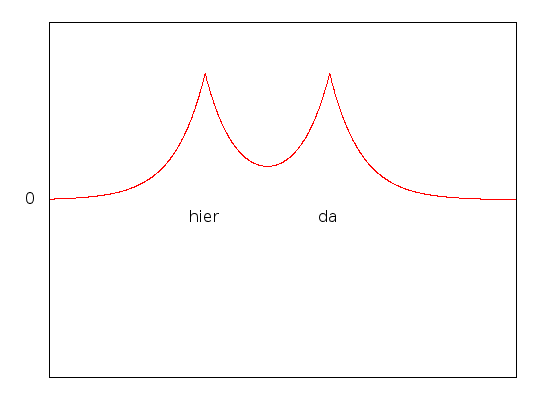
Wie ihr seht, ist sie in der Mitte zwischen den Protonen etwas größer geworden, so dass das Elektron das elektrische Feld sozusagen gut ausnutzt. Der Effekt wird noch stärker, wenn wir die beiden Protonen dichter zusammenrücken lassen:
Allerdings sollten die beiden Protonen auch nicht zu eng zusammenrücken – denn sie sind ja positiv geladen und stoßen sich ab. Es gibt also irgendwo einen besonders günstigen Abstand der beiden Protonen, und nur den betrachten wir jetzt. Dank unseres Elektrons sind die Protonen jetzt aneinander gebunden, weil ja die Energie der beiden protonen kleiner ist, wenn sie zusammen sind, als wen sie es nicht sind. Wir haben ein ganz einfaches Molekül gebaut, das aus zwei Protonen und einem Elektron besteht. Da ein Elektron und ein Proton zusammen ein Wasserstoff-Atom bilden, haben wir also zwei Wasserstoffatome verbunden, allerdings fehlt ein Elektron, Was wir gebaut haben ist ein H2+-Molekül. (Nebenbei habt ihr also gleich gesehen, wie man chemische Bindungen mit Hilfe der Quantenmechanik verstehen kann – eigentlich wollte ich das gar nicht erklären…)
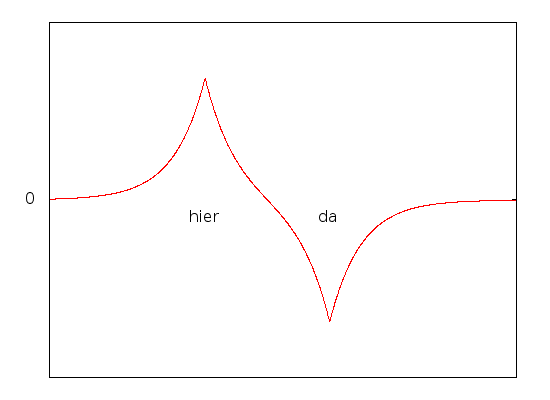
Umgekehrt gibt es auch einen energetisch besonders ungünstigen Zustand (das ist auch genau der, den ich oben für die Aufgabe gezeichnet hatte)
Hier sieht die Wellenfunktion etwa so aus:
und die Wahrscheinlichkeit, das Elektron da zu treffen wo es energetisch günstig ist (nämlich zwischen den Protonen) ist besonders klein.
(Kleine Anmerkung: Natürlich gibt es noch andere Zustände des Elektrons, bei denen die Wellenfunktion anders aussieht, die betrachte ich hier aber nicht. Ich beschränke mich auf die Kombination des “hier”- und des “da”-Zustands.)
Wir können diese beiden Zustände in unser Diagramm einzeichnen:
Statt “hier” und “da” als Achsen zu nehmen, könnten wir genauso gut die beiden Energie-Zustände als Achsen nehmen:
Wie ihr seht, können wir auch umgekehrt den Zustand |hier> über die beiden anderen Zustände ausdrücken:
Kleine Übung: Wie wird der Zustand |da> ausgedrückt?
Antwort:
Ihr könnt einen beliebigen Zustand also auf zwei unterschiedliche Arten hinschreiben: Entweder als Überlagerung aus |hier> und |da> oder als Überlagerung aus |Grundzustand> und |ungünstiger Zustand> – jeder Punkt auf der Kreislinie kann entweder in der einen oder der anderen Weise ausgedrückt werden.
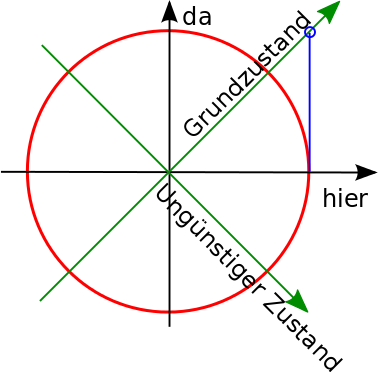
Aufgabe: Könnt ihr einen beliebigen Zustand auch über eine Kombination von |da> und |Grundzustand> ausdrücken? Versucht es als Beispiel mit dem Zustand |hier>.
Antwort: Ja, das geht, es ist aber ein bisschen trickreich.
Ihr könnt den “hier”-Zustand erreichen, wenn ihr erst auf der Grundzustands-Linie bis zum blauen Kringel geht und dann von dort aus senkrecht nach unten. Mathematisch bekommt ihr den Zustand durch
Macht euch keine Sorgen, wenn ihr das nicht auf die Schnelle ausrechnen konntet, es gehört ein bisschen Übung dazu, auch wenn es nicht wirklich schwer ist: In der Grafik hat der Zustand “hier” die Koordinaten (1,0), der Zustand “da” die Koordinaten (0,1) und der “Grundzustand” die Koordinaten (1/√2, 1/√2). Ihr müsst jetzt Zahlen finden, so dass der Grundzustand und der da-Zustand mit diesen Zahlen multipliziert und dann addiert gerade (1,0) ergeben. Um den zweiten Koordinatenwert auf Null zu bekommen, muss der Faktor des “da”-Zustands um √2 größer sein als der Faktor des Grundzustands (und die beiden müssen umgekehrtes Vorzeichen haben), außerdem muss der Faktor des Grundzustands gleich √2 sein, damit für die erste Koordinate 1 herauskommt. Die rechnerei ist aber hier wirklich nicht das entscheidende.






Kommentare (53)