Heute ist es endlich so weit: Wir gucken uns an, wie die berühmte quantenmechanische Verschränkung funktioniert.
Ein anderes Beispiel: Polarisation
Viele Experimente zur Quantenmechanik macht man mit Photonen, also den “Teilchen des Lichts”. (Fragt drei PhysikerInnen nach der genauen Definition eines Photons, und ihr bekommt vermutlich vier verschiedene Antworten, deswegen setze ich die Erklärung mit den Lichtteilchen in Anführungsstriche. Der berühmte Physiker Lamb hat sogar mal einen Artikel mit dem Titel “Anti-Photon” geschrieben, in dem er schreibt “Only a comedy of errors and historical accidents led to its popularity among physicists and optical scientists. ” Aber keine Sorge, euch können diese Feinheiten hier erstmal egal sein, irgendwann schreibe ich auch darüber mal was (das gehört ja eigentlich in die momentan in Warteschleife liegende Quantenfeldtheorie-Serie)…)
Ja, also zurück zu den Photonen. Wir machen uns das Leben hier einfach und betrachten eine Lichtquelle, die sehr schwaches Licht aussendet. Lässt man dieses Licht auf einen Sensor fallen und misst die Energie, dann stellt man fest, dass die Energie quantisiert ist – die Energie kommt in Paketen, deren Größe von der Lichtwellenlänge abhängt: Je kleiner die Wellenlänge, desto größer die Energie eines Pakets. (Das ist übrigens auch der Grund, warum ihr mit wenig UV-Strahlung einen Sonnenbrand bekommen könnt, mit beliebig viel sichtbarem Licht aber nicht: Die Energiepakete des sichtbaren Lichts reichen nicht aus, um die Haut zu schädigen.) Für diese Erklärung (also die der Energiepakete, nicht das mit dem Sonnenbrand) hat Einstein übrigens seinen Nobelpreis bekommen.
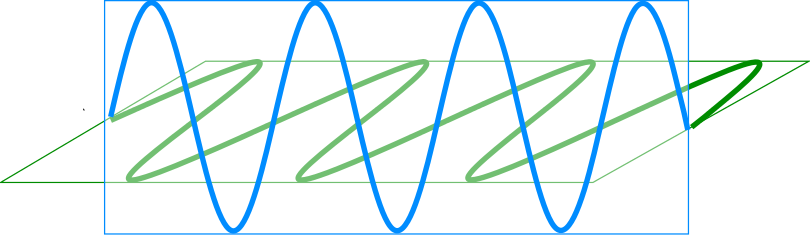
Mich interessiert hier aber eine andere Eigenschaft der Photonen, nämlich ihre Polarisation. Photonen sind ja die Teilchen, aus denen elektromagnetische Wellen bestehen. (Das ist seehr salopp gesagt – in eine rkohärenten elektromagnetischen Welle ist die Zahl der Photonen nicht mal genau definiert, das darf euch hier aber egal sein) Das elektrische Feld schwingt dabei senkrecht zur Richtung, in der sich das Licht ausbreitet (wenn ihr gern toll klingende Fachwörter mögt: Man nennt das eine “Transversalwelle”). Nehmt an, das Licht fliegt entlang einer bestimmten Achse (im Bild nach rechts), dann ist die Schwingungsrichtungrichtung des elektrischen Feldes nach oben/unten (blau) oder nach vorn/hinten (grün):
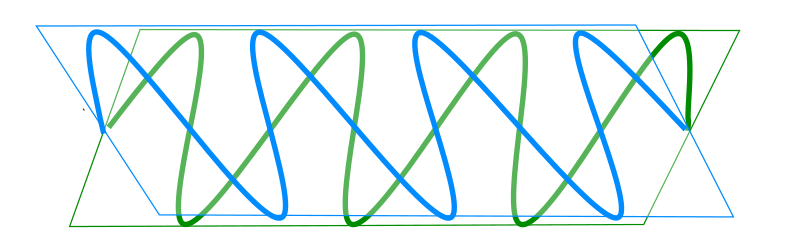
Das Photon kann auch unter einem Winkel polarisiert sein, beispielsweise unter 45° nach schräg vorn oder schräg hinten (ich hoffe, die Perspektive ist einigermaßen zu erkennen):
Man kann die Polarisation eines Photons also über einen Winkel angeben – da das elektrische Feld immer senkrecht zur Ausbreitungsrichtung ist, kann man beispielsweise sagen: Ein Photon ist senkrecht polarisiert, oder waagerecht, oder unter einem Winkel von 45°. Die zugehörigen Zustände schreibe ich hier mit kleinen Pfeilen, weil das schön anschaulich ist:
Senkrecht polarisiert 
waagerecht polarisiert 
unter -45° 
unter +45° 
Anmerkung für die ganz Genauen: Ich betrachte hier nur sogenannte lineare Polarisation. Es gibt auch zirkular polarisiertes Licht – das könnten wir mit unserem angehäuften Wissen auch verstehen, wir brauchen es hier aber nicht – Verschränkung ist ja im Moment unser Ziel.
Polarisationen kann man leicht messen: Dazu schickt man ein Photon durch einen Polfilter. Ein Polfilter hat auch eine Richtung, genau wie die Polarisation des Photons selbst. Ist eine elektromagnetische Welle genau parallel zum Polfilter orientiert, dann lässt er sie ungehindert durch, ist sie senkrecht polarisiert, dann kommt sie nicht durch:
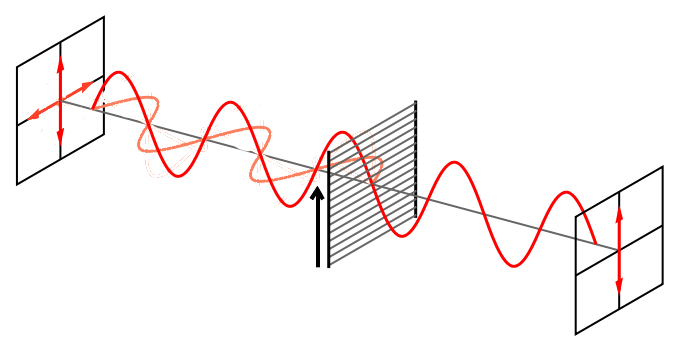
Bild von Bob Mellish. (modifiziert) Creative Commons Attribution-Share Alike 3.0 Unported license.
(Lasst euch nicht von den Linien auf dem Polfilter irritieren – die Richtung des Polfilters ist senkrecht zu den gezeichneten Linien, deshalb habe ich noch einen Pfeil in das Wikipedia-Bild eingebaut.)
Kommentare (122)