Der Polfilter misst also den Zustand eines Photons: Ein Photon, das vertikal polarisiert ist, wird also niemals im Zustand “horizontal polarisiert” gemessen (es kommt niemals durch einen horizontal orientierten Polfilter) und umgekehrt. Ist die Polarisationsrichtung +45° (also nach rechts oben), dann kommt das Photon niemals durch einen Polfilter, der mit -45° orientiert ist und umgekehrt.
Und was passiert, wenn der Polfilter und die Polarisationsrichtung des Photons irgendwie zueinander verdreht sind? Zum Beispiel, wenn mein Photon in senkrechter Richtung polarisiert ist und ich es durch einen Filter schicke, der um +45° gedreht ist?
Wir können den Polarisationszustand des Photons in ein Diagramm eintragen:
Erinnert euch das an etwas? Die Situation ist genau analog zu der mit den Orts- und Energie-Zuständen aus dem letzten Teil. Vielleicht könnt ihr ja erraten, was passiert?
Den Zustand “senkrecht polarisiert” kann ich zusammensetzen aus “polarisiert unter +45°” und “polarisiert unter -45°”:
Also hat das Photon eine Wahrscheinlichkeit von 50%, dass es durch den Filter unter +45° durchkommt (und dann also im Zustand +45° ist) und eine 50%-Wahrscheinlichkeit, dass es nicht durchkommt (dann wäre es im Zustand -45°, aber nicht wirklich, weil es vom Polfilter absorbiert wurde und deshalb nicht mehr existiert. Es ist dahingeschieden. Ein Ex-Photon…)
Waagerecht polarisiert geht entsprechend (beachtet das Minus-Zeichen):
Sind Polfiltr und Polarisation des Photons um 45° gegeneinander verdreht, ist die Wahrscheinlichkeit, dass das Photon den Filter passiert, gerade 1/2, also das Quadrat der Amplitude. Das Nette an polarisierten Photonen ist also, dass man die unterschiedlichen Überlagerungen direkt geometrisch interpretieren kann und sofort sehen kann, wie die Zerlegung geht.
Als Übung könnt ihr ja mal versuchen, euch (vielleicht mit einer Zeichnung) zu überlegen, was passiert, wenn ich ein senkrecht polarisiertes Photon auf einen Polfilter schicke, der um einen anderen Winkel gedreht ist, zum Beispiel um 30°.
Wenn ihr es genau ausrechnet (und seinerzeit in der Schule bei der Trigonometrie gut aufgepasst habt), dann ist die Amplitude dafür, dass das Photon durch den Filter kommt, gleich dem Kosinus von 30°, die Amplitude für’s nicht-Durchkommen ist sin(30°). In Zahlen sind die Amplituden √3/2 und 1/2. Die Wahrscheinlichkeiten dazu könnt ihr durch Quadrieren bekommen, sie sind 3/4 und 1/4. Ist der Polfilter also nur wenig verdreht, ist die Wahrscheinlichkeit sehr hoch, dass das Photon durchkommt. Wenn man sehr viele Polfilter direkt übereinander stapelt und jeden ganz wenig gegen den davor verdreht, dann kann man die Polarisation des Lichts deswegen “mitdrehen”. Dieser Trick wird übrigens in jedem LCD-Bildschirm angewandt, weil die Flüssigkristalle wie kleine Polfilter wirken.
Dazu gibt es auch ein hübsches Bild bei Wikipedia:
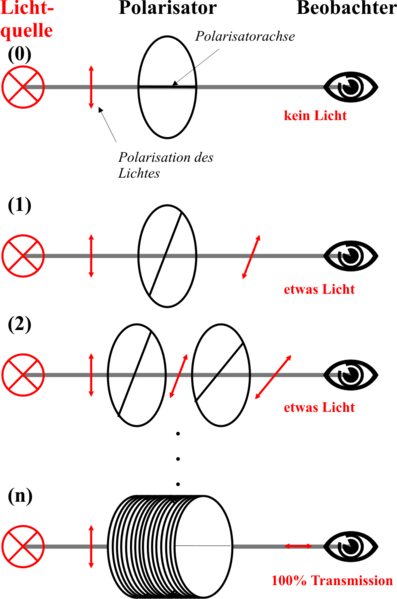
Von —Jkrieger 00:14, 17. Feb 2005 (CET) – selbst gezeichnet, Bild-frei, Link
Noch ein kleiner Tipp zum Lesen der Formeln (auch wenn sie euch jetzt im dritten Teil vermutlich nicht mehr schrecken): In vielen Formeln wie denen oben haben alle Summanden einen Vorfaktor 
Endlich: Verschränkung
Und jetzt habt ihr genug Wissen angehäuft, um zu verstehen, wie die berühmte quantenmechanische Verschränkung funktioniert. Warum es die Verschränkung gibt, kann ich euch auch nicht erklären – die Natur ist halt so merkwürdig. Aber wie man sie beschreibt, das könnt ihr jetzt hoffentlich relativ einfach verstehen.
Dazu brauchen wir zwei Photonen. Wir denken uns eine Quelle, die zwei Photonen aussenden kann, eins nach links und eins nach rechts. Dort messen wir (bzw. die beiden PhysikerInnen Alice und Bob, deren Job das traditionell ist) die Polarisation der Photonen.
Kommentare (122)