Zeitkristalle

Was klingt wie eine magische Zutat aus dem Geheimschrank von Professor Dumbledore ist eine der neusten Ideen aus der theoretischen Physik: Zeitkristalle. Es handelt sich nicht um kristallisierte Zeit, sondern um Kristalle, die sich in der Zeit so verhalten wie es normale Kristalle im Raum tun.

Um die Idee zu verstehen, muss man sich erst einmal fragen was ein gewöhnlicher Kristall (ein “Raumkristall”) eigentlich ist. In einem Kristall ordnen sich Atome (oder auch Moleküle, aber ich bleibe der Einfachheit halber bei Atomen) regelmäßig an, etwa so:

By H. Hoffmeister – first upload in de wikipedia on 17:21, 14. Okt 2005 by Lanzi, CC BY-SA 3.0, Link

Hier im Beispiel seht ihr einen Natriumchlorid-Kristall. Die beiden unterschiedlichen Atome sind jeweils elektrisch geladen und ziehen sich an, dürfen sich aber nicht zu nahe kommen, da sich ihre Elektronenhüllen bei zu kleinen Abständen abstoßen. Es bildet sich deshalb ein Gleichgewichtszustand aus, in dem die Atome regelmäßig angeordnet sind, so dass jedes von ihnen von vielen entgegengesetzten Ladungen umgeben ist. Dieser Zustand ist der energetisch günstigste (und generell tendieren Systeme ja dazu, ihre Energie zu minimieren).

Vom Standpunkt der theoretischen Physik aus ist an so einem Kristall eins besonders interessant: Er weist eine “spontan gebrochene Symmetrie” auf. Das Universum selbst ist ja an allen Orten zunächst mal gleich (es gibt keinen bevorzugten Raumpunkt) – es ist also symmetrisch gegen eine Ortsverschiebung. In einem Gas gilt das auch für die Atome – im statistischen Mittel finde ich an jedem Punkt mit gleicher Wahrscheinlichkeit ein Atom. In einem Kristall wie unserem hier ist das allerdings nicht mehr so – an einigen Orten sitzen Atome, an anderen nicht, die Symmetrie gegen eine beliebige Ortsverschiebung ist gebrochen. (Mehr über Symmetrie in der Physik findet ihr hier.) Der Kristall ist dabei periodisch, das heißt er wiederholt sich nach einem kleinen Stück immer wieder.

Betrachtet man die Sache etwas genauer und aus dem Blickwinkel der Quantenmechanik, sieht die Sache ein klein wenig komplizierter aus: Der energetisch günstigste Zustand ist der des Kristallgitters, aber wo genau das Kristallgitter sitzt, spielt für die Energie keine Rolle – verschiebe ich das Gitter oben im Bild etwas nach rechts oder links, dann ändert sich die Energie ja nicht. Quantenmechanisch gesehen ist das Kristallgitter also zunächst in einem Überlagerungszustand aus allen möglichen Orten – erst wenn ich die Position eines Atoms messe, dann weiß ich, wo das Gitter genau ist. Solange das Kristallgitter dabei perfekt ist, genügt eine einzige Messung an einem Ort, um die Position des gesamten Gitters festzulegen.

Anmerkung für die Physik-Nerds Laut dem Goldstone-Theorem ist mit jeder spontan gebrochenen kontinuierlichen Symmetrie eine Nullmode verbunden – im Kristall sind das die Phononen. Die Messung des Atoms muss also so vorsichtig gemacht werden, dass sie das Gitter nicht stört – da die Energie eines Phonons beliebig klein sein kann, heißt das (wenn ich es mir richtig überlegt habe – das habe ich so jedenfalls nirgends gelesen), dass ich wegen der Energie-Zeit-Unschärfe einen sehr langsamen Messprozess brauche.

Zusammengefasst haben wir also folgendes herausgefunden: Ein Kristall entsteht, weil ein periodischer Zustand mit gebrochener Symmetrie im Raum energetisch der günstigste Zustand ist. Weil es sich eben um eine Symmetrie im Raum handelt, können wir von einem “Raumkristall” sprechen.

Und damit ergibt sich ganz zwanglos die Definition eines “Zeitkristalls”: Ein Zeitkristall entsteht, wenn ein periodischer Zustand mit gebrochener Symmetrie in der Zeit der energetisch günstigste Zustand ist. Toll, oder? Fragt sich nur, was das heißen soll.

Fangen wir vorn an: Was ist ein periodischer Zustand mit gebrochener Symmetrie in der Zeit? Im Raumkristall war es so, dass wir entlang einer der Kristallachsen laufen können und sehen: Kein Atom -Atom – kein Atom – Atom usw. In der Zeit müsste es ähnlich sein. Wenn wir uns an einen ganz bestimmten Ort setzen und entlang der Zeitachse laufen (also einfach die Zeit vergehen lassen), sehen wir dort mal “kein Atom” und mal sehen wir eins. Da Atome nicht einfach so aus dem Nichts auftauchen und verschwinden können, klingt das erst mal ziemlich blöd.

Wir können das Konzept aber retten, wenn wir unseren Atomen erlauben, sich im Raum zu bewegen. Stellt euch vor, das Kristallgitter oben im Bild würde sich entlang einer der Achsen bewegen: Dann haben wir an einem bestimmten Ort mal ein Atom und mal nicht – ganz periodisch. Die Zeitsymmetrie (das Gitter sieht zu jedem Zeitpunkt genau gleich aus) wäre gebrochen. Ist das jetzt schon ein Zeitkristall? Das wäre ziemlich banal, wann immer ich mir Zucker in den Kaffee streue, würde ich dann einen “Zeitkristall” haben, weil sich ein Kristallgitter bewegt (o.k., ich müsste meine Zuckerkörnchen genau achsparallel in den Kaffee schütten, so zwanghaft bin nicht mal ich (auch wenn ich genaue Regeln zur Auswahl der richtigen Kaffeetasse habe…)). Aber das allein reicht nicht für einen Zeitkristall, denn der soll ja seine Zeitsymmetrie spontan brechen, um seine Energie zu minimieren, und dann bitte dauerhaft in diesem Zustand bleiben. (Nach den Regeln der Quantenmechanik ist es sonst kein energetisch eindeutiger Zustand.)

Für einen Zeitkristall brauchen wir also ein System, dass sich irgendwie spontan bewegt, weil das energetisch günstig ist. Eine Idee, wie das gehen könnte, hatte zunächst Frank Wilczek, aber da sein Konzept etwas schwer zu verstehen ist, verwende ich eine Variante seines Konzepts nach Li et al., die auch den Vorteil hat, dass man sie mit aktuellen Techniken realisieren können sollte.

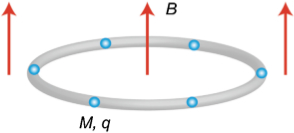
Dazu verwenden wir einzelne Ionen einer Atomsorte, die alle gleich geladen sind und sich deshalb abstoßen. Wir sperren diese Ionen mit Hilfe von passenden elektrischen Feldern so ein, dass sie die kleinst-mögliche Energie haben, wenn sie sich entlang eines Kreises anordnen:

Aus Li et al., s.u.

Da die Ionen sich gegenseitig abstoßen, werden sie auf dem Kreis einen “Kristall” bilden, bei dem sie alle brav denselben Abstand voneinander haben. Das ist ein Ringkristall, aber natürlich kein Zeitkristall, denn im Grundzustand bewegen sich die Ionen ja nicht.

Jetzt nutzen wir einen Trick aus der Quantenmechanik: Legt man ein schwaches Magnetfeld an, dann gibt es einen magnetischen Fluss durch den Ring. Die Regeln der Quantenmechanik besagen jetzt, dass ein geladenes Teilchen auf dem Ring nur dann stationär an seinem Ort verharren kann, wenn der Fluss durch den Ring ein Vielfaches des so genannten Flussquants ist. (Der Grund dafür ist ziemlich trickreich. Arg vereinfacht kann man so argumentieren: Damit ein Ion stationär auf dem Ring sitzen kann, muss seine Wellenfunktion entlang des Rings nach einem Umlauf wieder exakt denselben Wert bekommen, ohne dabei Sprünge zu haben. Legt man ein Magnetfeld an, dann beeinflusst das die Wellenfunktion, so dass das nicht mehr funktioniert. (Wer das deutlich genauer nachlesen will, kann unter den Stichworten “Aharanov-Bohm-Effekt” und “Berry-Phase” nachlesen.))

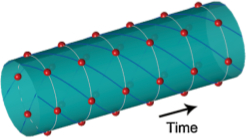
Legt man also ein schwaches Magnetfeld an, bei dem der Fluss durch den Ring kein Vielfaches des Flussquants ist, dann können die Ionen nicht mehr am Ort bleiben und müssen sich bewegen – dabei erzeugen sie ein Gegen-Magnetfeld, das dafür sorgt, dass der magnetische Fluss durch den Ring einen zulässigen Wert hat. So sieht unser Zeitkristall dann aus:

Aus Li et al., s.u.

Die Ionen laufen jetzt periodisch um den Ring herum. Aber ähnlich wie bei unserem Raumkristall ist die Sache wieder etwas komplizierter, wenn man die Quantenmechanik hinzuzieht – ohne weitere Beobachtung wird das System in einem Überlagerungszustand aus allen denkbaren umlaufenden Konfigurationen sein. Dann habe ich noch keinen Zeitkristall, weil die Wahrscheinlichkeit, ein Ion an einem bestimmten Ort zu messen, immer gleich groß ist. (So etwas kennt man übrigens schon lange von den Supraleitern, wo sich auch Ringströme um magnetische Flussschläuche bilden können.)

Damit ich einen Zeitkristall bekomme, muss ich (genau wie vorhin beim Raumkristall) eins der Ionen an einem bestimmten Ort messen, und zwar so, dass ich dabei den Zustand des Systems nicht störe. Wilczek hat sich dafür einen ziemlich komplizierten Mechanismus ausgedacht, Li et al. einen anderen, der sicherstellen soll, dass die Energie, die bei der Messung aufgewandt wird, so klein ist, dass der Zeitkristall erhalten bleibt.

Aber funktioniert das wirklich? Der Physiker Patrick Bruno hat beide Konzepte untersucht und ist zu dem Schluss gekommen, dass sowohl die Idee von Wilczek als auch der Ionenring nicht funktionieren können. Das Argument dazu beruht – wenn ich zumindest die Idee richtig verstehe – darauf, dass eine Messung immer ein Störpotential einführen müsste (beispielsweise könnte ich ja ein Photon einstrahlen, um eins der Ionen dingfest zu machen). Dieses Störpotential kann ein Ion aber nur dann an einem Ort festnageln, wenn es hinreichend stark ist, und dann beeinflusst es die Energie des Systems so sehr, dass der Grundzustand des Zeitkristalls gestört wird. (Ich übernehme keine Garantie dafür, dass ich das hier wirklich richtig verstanden habe – die sehr kurze Arbeit enthält ein trickreiches mathematisches Argument über die korrekte Reihenfolge von Grenzwertbetrachtungen (grusel).)

Gibt es also “Zeitkristalle” oder beruhen sie nur auf einem Rechenfehler? Warten wir’s ab – auf jeden Fall hat die theoretische Physik ein neues und faszinierendes Spielzeug Konzept.

Frank Wilczek, Quantum Time Crystals, https://arxiv.org/abs/1202.2539v2

T. Li et al., Space-Time Crystals of Trapped Ions, Phys. Rev. Lett., 109, 163001 (2012)

P. Bruno, “Comment on “Space-Time Crystals of Trapped Ions”: And Yet it Moves Not!, https://arxiv.org/abs/1211.4792

P. Bruno, Comment on “Quantum Time Crystals”: a new paradigm or just another proposal of perpetuum mobile? https://arxiv.org/abs/1211.4792

P. Colemann, Time Crystals, Nature Vol 493, S. 166