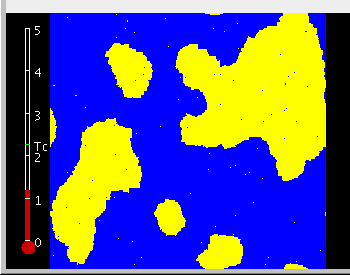
Bei niedriger Temperatur – einzelne Inseln einer Orientierung in einem Meer der anderen.
Etwas höhere Temperatur – die Ränder der Inseln werden rauer und im Innern der Inseln und des Meeres drehen sich einzelne Spins auch um.
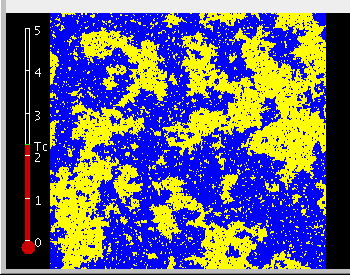
Genau am sogenannten kritischen Punkt: Es gibt Inseln aller Größenordnungen.
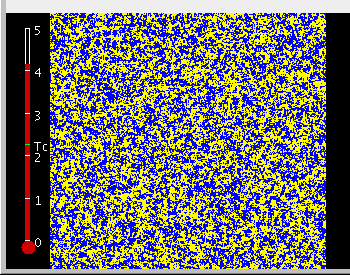
Bei sehr hoher Temperatur – die Spins sind im wesentlichen zufällig verteilt.
Ihr seht schon, da passiert ziemlich viel in diesem System, und darüber könnte ich sicher eine meiner gefürchteten Endlos-Serien schreiben.
Wir gucken aber nur auf Energie und Entropie; die Energie haben wir abgehakt, jetzt kommt die Entropie. Wir brauchen sie als Funktion der Energie, und das ist (wenn man nicht zu genau hinschaut) einigermaßen einfach: Die Entropie ist bestimmt durch die Zahl der Möglichkeiten, einen Zustand mit einer bestimmten Energie zu erreichen. Bei unserem Mini-Modell mit 100 Spins gibt es nur einen Zustand mit Energie -200, nämlich den, wo alle nach oben zeigen (alle nach unten ginge auch, aber das habe ich ja oben verboten!). Zur Energie -192 gibt es schon 100 Möglichkeiten, denn jeder der Spins kann derjenige sein, der umklappt. Bei Energie -184 sind zwei Spins umgeklappt, dafür gibt es 100 ⋅ 99/2 Möglichkeiten, denn ich habe erst 100 Möglichkeiten für den ersten Spin, dann 99 für den zweiten, aber es ist egal ob ich erst Spin 12 und dann Spin 76 ausgewählt habe oder umgekehrt, deshalb teile ich nochmal durch zwei (wobei ich die Tatsache außer acht lasse, dass ein Zustand mit zwei benachbarten umgeklappten Spins eine etwas niedrigere Energie hat, so genau müssen wir nicht hingucken). Ist Ω(E) die Zahl der Möglichkeiten zur Energie E, dann ist die Entropie definiert als
S= k ln Ω
Dabei ist k die berühmte Boltzmann-Konstante (eine Naturkonstante) und ln ist der (natürliche) Logarithmus. Die Formel ist die berühmte Boltzmansche Definition der Entropie, die auch auf seinem Grabstein steht (und über die ihr mehr erfahrt, wenn ihr rechts bei Artikelserien klickt und die Entropie-Serie lest).
Den Logarithmus nimmt man deswegen ,weil man möchte, dass die Entropie die folgende Eigenschaft hat: Habe ich zwei Systeme, dann soll die Entropie beider Systeme zusammen gleich der Summe der Einzelentropien sein. Nehmen wir an, das erste System hat 100 Möglichkeiten, das zweite auch. Betrachte ich beide zusammen, sind das dann 10000 Möglichkeiten (100 mal 100), also das Produkt der beiden Zahlen. Der Logarithmus hat aber nun gerade die Eigenschaft, dass er aus einem Produkt eine Summe macht, oder in Formeln ausgedrückt:
Das erklärt also, warum man den Logarithmus braucht; der zusätzliche Vorfaktor “Boltzmann-Konstante” hat mehr oder weniger historische Gründe, man hätte die Entropie auch ohne ihn definieren können. Man kann also sagen: die Entropie ist der Logarithmus der Zahl der Möglichkeiten für einen bestimmten Zustand bzw., in unserem Fall hier, für eine bestimmte Energie.
Und jetzt können wir uns die Funktion ΔS/ΔE angucken. Ist das System im Zustand niedrigster Energie, so gibt es nur eine Möglichkeit, die Entropie ist also ln(1)=0. Erhöhen wir die Energie um 8 Einheiten (auf -192), dann gibt es 100 Möglichkeiten, die Entropie ist jetzt also k ln(100). Für eine Energieänderung δE von 8 ergibt sich also eine Entropieänderung von ΔS von k ln(100). Den Faktor k lasse ich im Folgenden der Einfachheit halber weg – die Entropie ist dann also ln(100).
Erhöhen wir die Energie noch einmal um 8 Einheiten, dann haben wir jetzt (näherungsweise, siehe oben) 100 ⋅ 99/2 Möglichkeiten, die Entropie ist jetzt also
ln(100) + ln(99) – ln(2). (Der Logarithmus eines Quotienten ist die Differenz der Logarithmen.) Die Entropieänderung von Energie -192 auf -184 ist jetzt
ln(100)+ln(99) – ln(2) – ln(100) = ln(99) -ln(2), sie ist also kleiner geworden. Nach unserer Anfangsformel heißt das, dass die Temperatur unseres Systems jetzt höher geworden ist, denn die ist ja der Kehrwert der Entropieänderung.







Kommentare (29)