Nebenbemerkung für ganz Genaue: Die Funktion verläuft hier etwas sprunghaft, weil ich nur 100 Spins habe. Hätte man unendlich viele, so könnte man die Energie pro Volumen um beliebig kleine Werte ändern und alles wäre etwas glatter.
So geht es weiter. Wenn wir drei Spins umklappen, dann haben wir 100 ⋅ 99 ⋅ 98/(2⋅3) Möglichkeiten, die Entropieänderung von 2 auf drei umgeklappte Spins ist dann also ln(98)-ln(3), sie ist also wieder kleiner geworden und entsprechend ist die Temperatur noch höher.
So geht es also immer weiter, die Entropie unseres Systems steigt (wenn auch mit jedem ΔE immer weniger). Irgendwann erreichen wir den Zustand maximaler Entropie. Das ist der, der die größte Anzahl an Möglichkeiten hat. Hier gibt es im statistischen Mittel genauso viele Spins nach oben wie nach unten und auch benachbarte Spins sind nicht mehr miteinander korreliert, sondern ziemlich beliebig ausgerichtet.
Noch eine Nebenbemerkung für ganz ganz Genaue: Ich habe extra “ziemlich beliebig” und nicht “völlig beliebig” geschrieben, denn ich betrachte hier ja das Modell immer bei einer ganz festen Energie. Würde ich die Temperatur festhalten, dann wären kleine Schwankungen der Energie erlaubt; in dem Fall könnte man dann einfach sagen, dass man für jeden Spin eine Münze wirft, Kopf heißt oben, Zahl heißt unten. Durch thermische Schwankungen kann sich dann die Energie auch mal ein bisschen vergrößern oder verkleinern. Hält man die Energie genau fest, dann geht das aber natürlich nicht ganz so einfach. Für sehr große Systeme geht der Unterschied zwischen festgehaltener Energie und festgehaltener Temperatur aber gegen Null. (In der statistischen Physik spricht man vom “mikrokanonischen Ensemble”, wenn die Energie festgehalten ist, und vom “kanonischen Ensemble”, wenn die Temperatur festliegt. (Es gibt auch noch das großkanonische Ensemble, da darf sich die Teilchenzahl ändern, aber dafür liegt das chemische Potential fest, aber das führt nun wirklich total vom Thema ab (ich schreibe das eh nur, falls jemand sich irgendwo schlau lesen will, dann habt ihr wenigstens passende Stichworte (und ich klammere schon wieder so viel, deswegen mache ich jetzt alle Klammern auf einmal zu, nämlich mit einer eckigen Klammer (so macht man das in LISP (was eine Abkürzung für “long and incredibly slow programs” ist] Ende der Nebenbemerkung.
Beim Zustand mit höchstmöglicher Entropie hat diese also ein Maximum. Ich kann aber immer noch weiter Energie ins System stecken. Bei niedriger Temperatur war es ja so, dass die Entropie klein war, weil sich benachbarte Spins gern parallel ausrichten wollten. Wenn ich in mein System bei höchstmöglicher Entropie weiter Energie ins System reinstecke, dann fangen benachbarte Spins an, sich entgegengesetzt auszurichten. Damit kann ich die Energie weiter steigern, wobei die Entropie aber wieder abnimmt. Und schließlich erreiche ich einen Zustand, wo die Spins wie die Felder eines Schachbretts angeordnet sind: Jeder Spin oben ist von vier Spins unten umgeben. Das ist der Zustand mit der höchsten Energie – seine Entropie ist aber verschwindend (wenn ich wie am Anfang einen Spin festhalte, dann ist sie gleich Null, weil es nur eine Möglichkeit gibt – ansonsten gibt es zwei, weil ich einen beliebigen Spin ja entweder nach oben oder unten zeigen lassen kann).
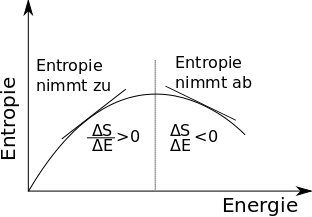
Die Entropie unseres Systems läuft also genau so, wie wir es letztes Mal aufgezeichnet haben (Wobei die Kurve am Anfang und am Ende genau senkrecht verlaufen müsste):
Noch einmal kurz zusammengefasst: Vom energetisch günstigsten Zustand aus stecken wir immer mehr Energie ins System. Dabei nimmt die Entropie immer weiter zu, aber mit jedem Energiebetrag ein bisschen weniger, so dass die Temperatur ebenfalls zunimmt. Irgendwann erreichen wir den Zustand maximaler Entropie, bei dem die Spins alle ungeordnet sind und sich nicht umeinander kümmern. Hier hat das System die Temperatur unendlich, denn am Maximum ist ΔS/ΔE ja gleich Null. Danach nimmt die Entropie wieder ab, die Temperatur springt also von plus unendlich auf minus unendlich (die Steigung ist ja sehr flach) und wird dann betragsmäßig immer kleiner, läuft also von minus unendlich gegen “minus Null”. Im Zustand maximaler Energie erreichen wir dann den absoluten Nullpunkt, aber von der negativen Seite aus.






Kommentare (29)