Um Prozesse bei Elementarteilchen zu beschreiben, verwendet man ja gern Feynmangraphen (oder Feynmandiagramme). Vermutlich hat kein anderes mathematisches Werkzeug so sehr Einzug in die Populärwissenschaft gefunden wie diese kleinen Bildchen. Sie sind einfach, anschaulich und wurden – anders als viele andere Veranschaulichungen – nicht speziell für Laien erfunden, sondern werden tatsächlich in der Physik benutzt. Leider haben sie auch einen entscheidenden Nachteil: Man kann sie extrem leicht falsch verstehen.
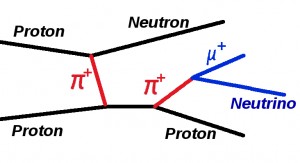
Hier erst einmal ein (extra kompliziertes) Beispiel für ein Feynmandiagramm
Die Zeitrichtung läuft hier von links nach rechts (manchmal auch von unten nach oben, da muss man aufpassen). Von links kommen also zwei Protonen, das eine sendet ein Teilchen (ein positives Pion) aus und wird dabei zu einem Neutron. Das andere Proton nimmt das Pion auf (und verandelt sich kurzfristig in ein Teilchen mit doppelter Ladung) und zerfällt dann wieder in ein Proton und ein Pion. Das Pion wiederum zerfällt in ein positiv geladenes Myon und ein Neutrino.
Eigentlich sind diese Graphen aber keine Bilder, sondern nichts als in Bilder umgeschriebene Gleichungen. (Wie man damit umgeht und so etwas prinzipiell berechnet habe ich vor seehr langer Zeit mal erklärt.) Mit diesen Gleichungen kann man berechnen, wie wahrscheinlich ein Prozess wie der oben dargestellte ist. (Generell gibt es in der Quantenwelt ja selten absolute Sicherheit, sondern nur Wahrscheinlichkeiten.)
Feynmangraphen sind ziemlich praktisch, weil sie es sehr leicht machen, sicherzustellen, dass man keine Möglichkeit für einen Prozess übersieht. Außerdem sind sie deutlich übersichtlicher als Gleichungen, weil die zweidimensionale Anordnung und das Verbinden von Punkten, an denen etwas passiert, mit Linien wesentlich einfacher zu überblicken ist als es eine einzelne Formel wäre – die für den dargestellten Prozess wäre schon ziemlich lang und unübersichtlich. (Obwohl Feynmangraphen so praktisch sind, soll der erste Vortrag von Feynman, in dem er sie vorgeführt hat, ein ziemlicher Flop gewesen sein. Man musste sich wohl erst mal an den Gedanken gewöhnen, statt Gleichungen Bildchen hinzumalen.)
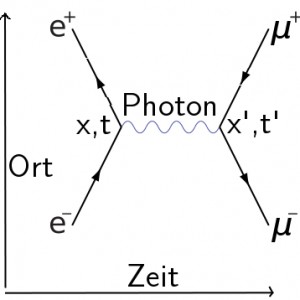
Feynmangraphen haben aber auch einen entscheidenden Nachteil: Sie verführen dazu, sie zu wörtlich zu nehmen. Nehmen wir dieses etwas einfachere Diagramm, in dem ein Elektron (e-, Pfeil in Zeitrichtung vorwärts) und ein Positron (e+, Pfeil in Zeitrichtung rückwärts) zu einem Photon werden, das dann wiederum in ein Myon und ein Anti-Myon zerfällt (das Bild stammt aus dem oben verlinkten Artikel, wo es wesentlich detaillierter erläutert wird als ich es hier tue (dezenter Hinweis…)):
Die beiden ankommenden Teilchen treffen sich am Ort x zur Zeit t – so sieht es jedenfalls aus. Aber in Wahrheit können wir den Prozess ja nicht im Detail beobachten – und schon gar nicht wissen wir, an welchem Ort sich die beiden Teilchen treffen. Wenn man bedenkt, dass es sich eigentlich um Quantenfelder handelt, nicht um Teilchen, und dass Elektron und Positron in Wahrheit eher wie zwei Wellen aussehen als wie zwei Punktteilchen, dann ergibt es gar nicht so schrecklich viel Sinn, von einem genauen Ort zu sprechen, an dem die Teilchen sich treffen. Das gleiche gilt für das eingezeichnete Photon: Scheinbar bewegt es sich vom Ort x zum Ort x’ – aber in Wahrheit ist auch das Photon eher eine Welle als ein Punktteilchen und ist über den Raum ausgebreitet.
Um den Prozess korrekt zu berechnen, muss man alle Möglichkeiten im Feynmandiagramm berücksichtigen – man muss also alle denkbaren Orte x und x’ (und auch alle möglichen Zeiten t und t’) in die Rechnung mit einbeziehen. Es wäre also zum Beispiel nicht richtig zu sagen, dass sich das Photon tatsächlich von einem bestimmten Ort zu einem bestimmten anderen bewegt, sondern es müssen alle Möglichkeiten in Betracht gezogen werden. Wir können auch nicht sagen, dass zur Zeit t”, die in der Mitte zwischen t und t’ liegt, ein Photon da ist – denn auch die Möglichkeit, dass sich die beiden Teilchen erst nach dem Zeitpunkt t” begegnet sind, müssen wir berücksichtigen.






Kommentare (21)