Die Physik ist ja voller abgefahrener und faszinierender Phänomene – Vakuumfluktuationen, negative Temperaturen, Quantenverschränkungen und und und. Aber heute schauen wir uns mal etwas ganz simples und einfaches an – ungefähr das einfachste physikalische Phänomen, das man sich vorstellen kann: Ein Teilchen fliegt von A nach B. (Danke an die Kommentatoren Loqi und Rainer Zufall, die mich mit klugen Fragen auf die Idee brachten, diesen Artikel zu schreiben.)
Um die Sache konkreter zu machen, stellen wir uns vor, dass vor uns auf dem Tisch zwei Detektoren stehen, mit denen man Elektronen messen kann. Die beiden Detektoren haben einen Abstand von einem Meter und können ein Elektron sehr genau lokalisieren (wir können uns zum Beispiel vorstellen, dass sie eine sehr kleine Kammer enthalten, in der die Lagun des Elektrons gemessen wird, oder eine Art Geigerzähler, oder sonst irgendetwas. Da es hier wirklich nur um die fundamentalen Grundlagen geht, lasse ich das einfach offen.) Wir ignorieren alle äußeren Einflüsse, über dem Tisch herrscht also Vakuum und der Tisch wiegt auch nichts und zieht deswegen das Elektron nicht an oder sonst etwas. Wir haben also wirklich nur ein Elektron zwischen zwei Punkten A und B.
Genau um 12:00:00Uhr messen wir das Elektron im Detektor A und um 12:00:01Uhr im Detektor B, einen Meter entfernt. Das Elektron (oder allgemein das Teilchen) hat sich also von A nach B bewegt. Wie beschreibt man diesen unglaublich simplen Sachverhalt in den unterschiedlichen physikalischen Theorien und was hat das Elektron laut diesen Theorien zwischendurch gemacht?
Klassische Physik
Fangen wir erst mal mit der klassischen Physik an, die ihr vermutlich mal in der Schule gelernt habt und laaaangweilig fandet.
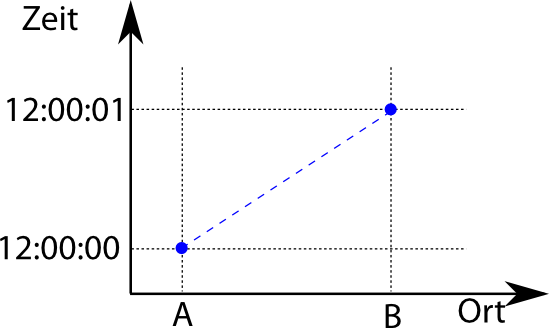
Nach den Regeln der klassischen Physik (die newtonschen Axiome) bewegt sich ein Elektron, auf das keine Kräfte wirken, mit konstanter Geschwindigkeit. Wenn es also um 12:00:00Uhr bei A war und um 12.00:01Uhr bei B in einem Meter Entfernung, dann hat es in einer Sekunde eine Strecke von einem Meter zurückgelegt und sich somit mit einer Geschwindigkeit von 1m/s bewegt. Entsprechend kann ich ausrechnen, wo das Elektron zwischendurch war und kann es z.B. in ein Diagramm einzeichnen:
Ort und Geschwindigkeit unseres Elektrons sind also zu jedem Zeitpunkt festgelegt.
Wenn ihr Lust habt, könnt ihr die Formeln nehmen, die man in allen Physik-Schulbüchern findet, und zum Beispiel die kinetische Energie (also die Bewegungsenergie) des Elektrons ausrechnen. Dafür gilt die Formel E=(1/2) m v². (Da die Masse des Elektrons sehr klein ist, ist seine Energie in diesem Fall extrem winzig, etwa 0,00000000000000000000000000000045 Joule, wenn ich mich bei den Nullen nicht verzählt habe…)
Mehr gibt es in der klassischen Physik dazu nicht zu sagen.
Oder doch?
Bezugssysteme
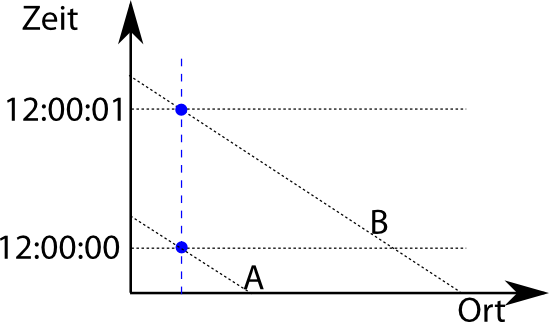
Stellt euch eine zweite Beobachterin vor, die sich mit einem Meter pro Sekunde in dieselbe Richtung bewegt wie das Elektron. Für sie stellt sich das Experiment anders dar: Das Elektron steht still und der Tisch mit den beiden Detektoren ist es, der sich bewegt. Ihr Diagramm, das beschreibt, was das Elektron tut, sieht entsprechend anders aus:
Wenn sich das Elektron im Tisch-System von links nach rechts bewegt, dann bewegen sich die Detektoren A und B im System der Beobachterin von rechts nach links, ihre Linien sind also andersherum geneigt.
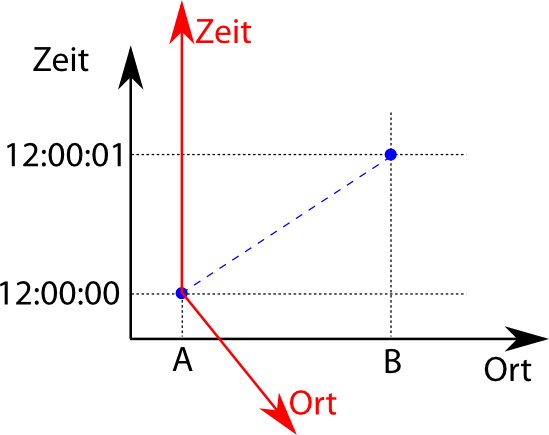
Ihr könnt auch, das, was die Beobachterin sieht, in euer Diagramm mit einzeichnen, das sähe dann etwa so aus (wobei die Regel hier so ist, dass Linien für konstante Orte senkrecht auf der roten Orts-Linie stehen; unten, wenn es um die Relativitätstheorie geht, sieht das etwas anders aus)::
Die Zeitachse ist euch und die mitbewegte Beobachterin dieselbe, aber die Ortsachse liegt für sie anders. (Damit keine Missverständnisse aufkommen – euer System ist nicht dadurch ausgezeichnet, dass Ort und Zeit genau senkrecht stehen – wenn die mitbewegte Beobachterin die Grafik zeichnet, dann sind es ihre Achsen, die senkrecht aufeinander stehen und eure, die verzerrt sind.)






Kommentare (27)