Wir betrachten also alle denkbaren Möglichkeiten in unsere Diagramm, wie das Elektron in der richtigen Zeit von A nach B kommen kann. (Anmerkung für die Physik-Nerds: Vermutlich müssen die Pfade eigentlich stetig differenzierbar sein und dürfen keine scharfen Knicks aufweisen; ganz sicher bin ich mir da allerdings nicht. Da das aber für das prinzipielle Verständnis egal ist, kümmere ich mich um solche Details hier nicht.)
Für jeden dieser Wege berechnen wir jetzt eine spezielle Größe, die Wirkung genannt wird. (Dieser Begriff ist sehr unglücklich gewählt, denn mit dem, was man im Alltag als “Wirkung” bezeichnet, hat diese Wirkung so ziemlich nichts zu tun.) Dazu messen wir zu jedem Zeitpunkt die kinetische Energie des Elektrons und addieren all diese Werte auf (mathematisch korrekt muss man über die Zeit integrieren). Derjenige Weg, bei dem die Wirkung am kleinsten ist, ist der, den das Elektron tatsächlich nimmt. (Wenn auf das Elektron noch Kräfte wirken, dann muss man die ebenfalls in der Wirkung berücksichtigen, aber das tun wir nicht.)
Dass das wirklich der Weg ist, bei dem das Elektron mit konstanter Geschwindigkeit auf geradem Weg fliegt, kann man leicht einsehen: Jeder Umweg bedeutet, dass das Elektron seine mittlere Geschwindigkeit erhöhen muss, also erhöht sich auch die mittlere Energie und damit die Wirkung. Das Elektron muss also den geraden Weg nehmen. Und von allen Möglichkeiten, den geraden Weg zu nehmen, ist die Wirkung dann am kleinsten, wenn die Geschwindigkeit konstant ist – denn ein Stück mit langsamer Geschwindigkeit muss ja mit einem mit hoher Geschwindigkeit kompensiert werden. Da in die kinetische Energie aber das Quadrat der Geschwindigkeit eingeht, ist das immer ungünstiger als die konstante Geschwindigkeit.
Ihr könnt euch das Leben auch – mit Hilfe der Beobachterin von vorhin – noch einfacher machen: Im Bezugssystem des Elektrons ist der Weg mit der kleinsten Energie logischerweise der, wo das Elektron brav auf der Stelle sitzt und darauf wartet, dass Detektor B vorbeikommt, da ist die Wirkung gleich Null. Wenn das in diesem System so gilt, dann muss es auch im Tisch-System gelten, also muss das Elektron mit konstanter Geschwindigkeit fliegen.
So, damit ist nun aber wirklich im Rahmen der klassischen Physik alles gesagt, was es zu sagen gibt.
Relativitätstheorie
Verlassen wir die “ganz” klassische Physik und schauen wir, wie sich das Bild ändert, wenn wir zur Relativitätstheorie übergehen. (Ich mache hier keinen Unterschied zwischen spezieller und allgemeiner RT, weil hier keine Schwerefelder wirken und deswegen beide Theorien dasselbe sagen – mehr zur Allgemeinen RT findet ihr, wenn ihr rechts bei “Artikelserien” klickt, da gibt es eine Serie zur Raumzeitkrümmung.) Warnhinweis: Falls hier jemand der üblichen Verdächtigen in den Kommentaren etwas über “Deppenphysik” und “Warum die RT Quatsch ist” schreiben will – ich werde solche Kommentare vermutlich schlicht löschen, weil ich keine Lust auf immer den gleichen Blödsinn habe.
Ich habe die RT hier übrigens generell etwas kurz abgehandelt, weil sie für die folgenden Betrachtungen zur Quantenphysik nicht ganz so wichtig ist.
In der Relativitätstheorie passiert etwas Ähnliches wie oben, als wir unsere Sicht der Dinge mit der der mitbewegten Beobachterin verglichen haben. Dort war es ja so, das wir uns zwar einige darüber waren, zu welchem Zeitpunkt das Elektron bei A und B war, aber nicht, was die relativen Positionen waren.
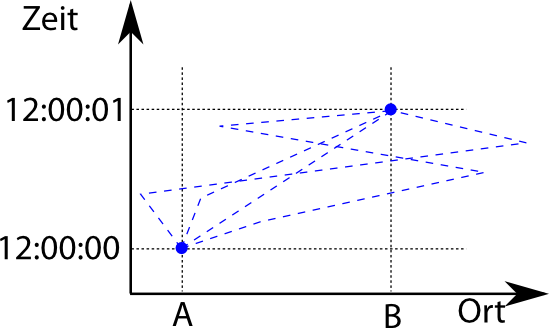
In der Relativitätstheorie ändert sich jetzt auch die Zeitwahrnehmung – die mitbewegte Beobachterin hat eine etwas andere Zeitwahrnehmung als wir, das ist die berühmte Zeitdilatation. Im Raumzeit-Diagramm verkippt sich dabei auch die Zeitachse, wobei die folgende Darstellung nur schematisch zu verstehen ist, sie ist quantitativ absolut falsch, denn bei Geschwindigkeiten von 1m/s ist der Unterschied im Zeitablauf extrem winzig (Sorry, hier war erst ein falsches Bild, ich hoffe, diese Version stimmt jetzt einigermaßen):






Kommentare (27)