In dieser kleinen Serie schaue ich mir das so ziemlich simpelste physikalische Phänomen an, das es gibt: Ein Teilchen (z.B. ein Elektron) fliegt von A nach B.Im letzten Teil haben wir uns angeschaut, wie man das Verhalten des Teilchens in der Quantenmechanik (QM) beschreibt: Das Teilchen hat eine Aufenthaltswahrscheinlichkeit, die bei einer Messung am Detektor A dort lokalisiert ist und dann zerläuft. Wir haben auch gesehen, wie diese Beschreibung und die der klassischen Physik ineinander übergehen: Wenn das Teilchen hinreichend schwer ist, dann zerläuft seine Aufenthaltswahrscheinlichkeitsfunktion (tolles Wort, oder?) nur vergleichsweise langsam und sie bewegt sich ähnlich wie ein klassisches Teilchen.
Es gibt aber noch eine ganz andere Sichtweise der Dinge – sie ist mathematisch äquivalent zur Beschreibung mit Aufenthaltswahrscheinlichkeiten, ist aber konzeptionell ganz anders gestrickt. Das ist das so genannte “Pfadintegral”.
Um das zu verstehen, müsst ihr noch einmal an den ersten Teil der Serie zurückdenken. Dort haben wir gesehen, dass man in der klassischen Physik das Prinzip der kleinsten Wirkung verwenden kann, um den Weg des Teilchens von A nach B zu beschreiben: Man betrachtet alle denkbaren Wege von A nach B
Der Weg, den das Teilchen tatsächlich geht, ist der mit der minimalen Wirkung. “Wirkung” ist dabei nicht das, was man sich im Alltag darunter vorstellt (der Weg der minimalen Wirkung ist nicht der, bei dem das Teilchen wenig “bewirkt” oder so), sondern einfach ein physikalischer Fachausdruck für eine bestimmte Größe. In unserem einfachen Fall eines Teilchens, das kräftefrei unterwegs ist, ist die Wirkung die Summe über die kinetische Energie zu jedem Zeitpunkt. Mathematisch genauer spricht man vom Integral über die Wirkung (Nachtrag: wie Kommentator Bjoern richtig bemerkt, stimmt das nicht wirklich, es sollte eher Integral über die kinetische Energie oder allgemein über die Lagrangefunktion heißen, aber ich bin hier etwas schludrig) – aber ihr könnt euch einfach vorstellen, dass ihr zu jeder Mikrosekunde einmal die kinetische Energie des teilchens messt und diese ganzen Energien addiert (und am Ende passend normiert, indem ihr durch die Zahl der Messungen teilt, damit immer etwa dasselbe rauskommt, egal ob ihr jede Mikrosekunde oder alle zwei Mikrosekunden messt).
In der klassischen Physik war es jetzt so, dass das Teilchen den Weg mit der kleinsten Wirkung nimmt, fertig. (Falls jemand ganz pingelig sein will: Ein Weg mit extremaler Wirkung geht auch, das ist aber nur selten praktisch relevant.) In der QM sind die Spielregeln etwas komplizierter.Wir haben ja schon im letzten Teil gesehen, dass man in der QM Wahrscheinlichkeitsaussagen macht, keine deterministischen Vorhersagen. Die Wahrscheinlichkeit, dass das Teilchen erst bei A dann bei B gemessen wird, konnten wir über die Wahrscheinlichkeitsverteilung darstellen, die am Anfang (nach der Messung bei A) einen Wert hatte und dann zerlief. Berechnen kann man das mit der Schrödingergleichung, das habe ich aber nicht vorgeführt (zumal es dazu auch ne ganze Artikelserie gibt…).
Auch in unserer neuen Darstellung mit dem Pfadintegral kann man die Wahrscheinlichkeit dafür berechnen, dass das Teilchen von A nach B läuft. Dazu betrachtet man, wie gesagt, jeden möglichen Weg und berechnet dessen Wirkung. Mathematisch kann man das, was hier passiert, sehr elegant mit komplexen Zahlen darstellen (das habe ich z.B. in meiner QFT-Serie auch so gemacht), aber anschaulicher ist es, man hantiert mit kleinen Pfeilen.
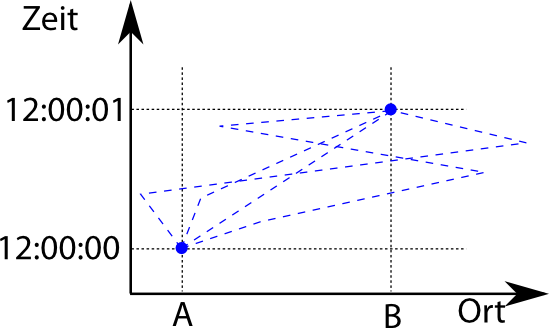
Jeder mögliche Weg von A nach B bekommt also einen kleinen Pfeil zugeordnet, den ihr euch wie einen Zeiger an einer Uhr vorstellen könnt.. Am Anfang (um 12:00:00 bei A) zeigt der Pfeil für alle Wege genau nach rechts. (Ihr könnt ihn auch woanders hinzeigen lassen, das ist egal – Hauptsache, ihr macht es für alle Wege gleich.) Jetzt verfolgt ihr den gerade betrachteten Weg von A nach B und lasst den Pfeil dabei rotieren (typischerweise gegen den Uhrzeigersinn). Wie schnell der Pfeil zu einem bestimmten Zeitpunkt rotiert, hängt von der Wirkung ab – teilt die Wirkung durch das Plancksche Wirkungsquantum h, und ihr erhaltet den Wert der Rotationsgeschwindigkeit (in Einheiten von Radiant pro Sekunde, falls es jemand genau wissen will). Ihr lauft also den Weg des Teilchens ab und lasst den Pfeil rotieren, und zwar um so schneller, je größer die Wirkung jeweils ist. (Nachtrag: wieder etwas schludrig, genauer ist es das Wirkungsinkrement oder die Lagrangefunktion, siehe den Kommentar unten) Das kann man sich etwa so veranschaulichen (das Bild ist nur qualitativ zu verstehen, ich habe nichts wirklich durchgerechnet und für ein reales Teilchen dreht sich der Pfeil viele viele Millionen mal in der Sekunde):






Kommentare (43)